Mehrfache lineare Regression in R [mit Grafiken und Beispielen]

Als Data Scientist werden Sie in vielen Projekten häufig gebeten, prädiktive Analysen durchzuführen. Eine Analyse ist ein statistischer Ansatz, um eine Beziehung zwischen einer abhängigen Variablen und einer Reihe unabhängiger Variablen herzustellen. Dieses ganze Konzept kann als lineare Regression bezeichnet werden, die im Wesentlichen aus zwei Arten besteht: einfache und multiple lineare Regression.

R ist eine der wichtigsten Sprachen in Bezug auf Data Science und Analytics, und so ist die multiple lineare Regression in R wertvoll. Es beschreibt das Szenario, in dem eine einzelne Antwortvariable Y linear von mehreren Prädiktorvariablen abhängt.

Was ist eine lineare Regression?

Lineare Regressionsmodelle werden verwendet, um die Beziehung zwischen a zu zeigen oder vorherzusagen abhängige und eine unabhängige Variable. Wenn in der Regressionsanalyse zwei oder mehr unabhängige Variablen verwendet werden, ist das Modell nicht einfach linear, sondern ein multiples Regressionsmodell.

Die einfache lineare Regression wird verwendet, um den Wert einer Variablen unter Verwendung einer anderen Variablen vorherzusagen. Eine gerade Linie stellt die Beziehung zwischen den beiden Variablen mit linearer Regression dar.

Bei der multiplen Regression besteht eine lineare Beziehung zwischen einer abhängigen Variablen und zwei oder mehr unabhängigen Variablen. Die Beziehung kann auch nichtlinear sein, und die abhängigen und unabhängigen Variablen folgen keiner geraden Linie.

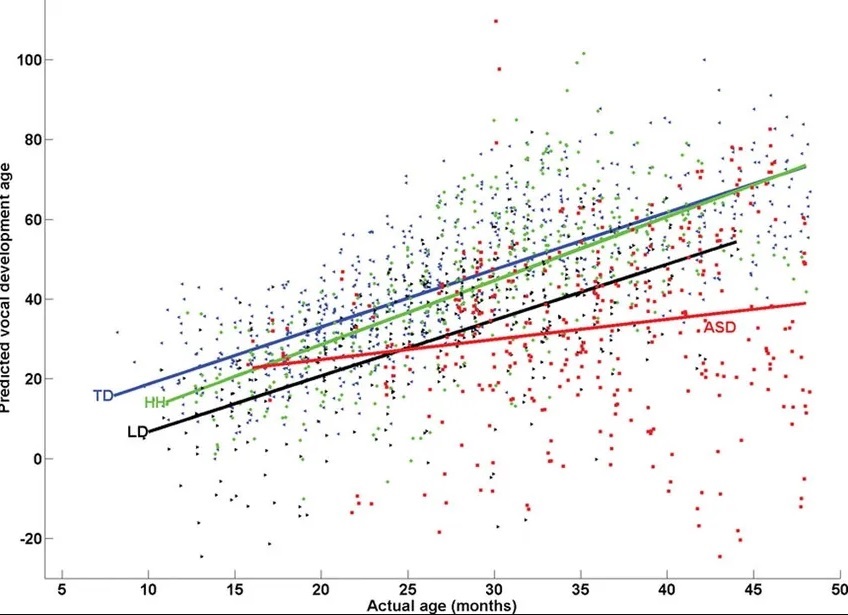
Bildliche Darstellung von Vorhersagen des multiplen linearen Regressionsmodells

Lineare und nichtlineare Regression werden verwendet, um eine Antwort unter Verwendung von zwei oder mehr Variablen zu verfolgen. Die nichtlineare Regression wird aus Annahmen von Versuch und Irrtum erstellt und ist vergleichsweise schwierig durchzuführen.

Was ist multiple lineare Regression?

Die multiple lineare Regression ist eine statistische Analysetechnik, die verwendet wird, um das Ergebnis einer Variablen basierend auf zwei oder mehr Variablen vorherzusagen. Sie ist eine Erweiterung der linearen Regression und wird auch als multiple Regression bezeichnet. Die vorherzusagende Variable ist die abhängige Variable, und die Variablen, die zum Vorhersagen des Werts der abhängigen Variablen verwendet werden, sind als unabhängige oder erklärende Variablen bekannt.

Die multiple lineare Regression ermöglicht es Analysten, die Variation des Modells und den relativen Beitrag jeder unabhängigen Variablen zu bestimmen. Es gibt zwei Arten von multipler Regression, lineare und nichtlineare Regression.

Multiple Regressionsformel

Die multiple Regression mit drei Prädiktorvariablen (x), die die Variable y vorhersagen, wird durch die folgende Gleichung ausgedrückt:

y = z0 + z1*x1 + z2*x2 + z3*x3

Die „z“-Werte stellen die Regressionsgewichte dar und sind die Beta-Koeffizienten . Sie sind die Assoziation zwischen der Prädiktorvariablen und dem Ergebnis.

• yi ist eine abhängige oder vorhergesagte Variable
• z0 ist der y-Achsenabschnitt, dh der Wert von y, wenn x1 und x2 0 sind
• z1 und z2 sind die Regressionskoeffizienten, die die Änderung von y in Bezug auf eine Änderung von x1 bzw. x2 um eine Einheit darstellen.

Annahmen der multiplen linearen Regression

Wir kennen die Kurzbeschreibung der multiplen Regression und die Grundformel. Es gibt jedoch einige Annahmen, auf denen die multiple lineare Regression basiert, wie im Folgenden beschrieben:

ich. Beziehung zwischen abhängigen und unabhängigen Variablen

Die abhängige Variable bezieht sich linear auf jede unabhängige Variable. Zur Überprüfung der linearen Zusammenhänge wird ein Scatterplot erstellt und auf Linearität beobachtet. Wenn die Scatterplot-Beziehung nichtlinear ist, wird eine nichtlineare Regression durchgeführt oder die Daten werden unter Verwendung von Statistiksoftware übertragen.

ii. Die unabhängigen Variablen sind nicht stark korreliert

Die Daten sollten keine Multikollinearität aufweisen, was passiert, wenn die unabhängigen Variablen stark miteinander korrelieren. Dies führt zu Problemen beim Abrufen der spezifischen Variablen, die zur Varianz in der abhängigen Variablen beiträgt.

iii. Die Restvarianz ist konstant

Bei der multiplen linearen Regression wird davon ausgegangen, dass der Fehler der verbleibenden Variablen an jedem Punkt des linearen Modells ähnlich ist. Dies wird als Homoskedastizität bezeichnet. Wenn die Datenanalyse abgeschlossen ist, werden die Standardresiduen gegen die vorhergesagten Werte aufgetragen, um zu bestimmen, ob die Punkte richtig über die Werte der unabhängigen Variablen verteilt sind.

iv. Beobachtungsunabhängigkeit

Die Beobachtungen sollten voneinander abhängen, und die Residuenwerte sollten unabhängig sein. Die Durbin-Watson-Statistik eignet sich dafür am besten.

Die Methode zeigt Werte von 0 bis 4, wobei ein Wert zwischen 0 und 2 eine positive Autokorrelation und ein Wert zwischen 2 und 4 eine negative Autokorrelation anzeigt. Der Mittelpunkt, ein Wert von 2, zeigt an, dass es keine Autokorrelation gibt.

v. Multivariate Normalität

Multivariate Normalität tritt bei normalverteilten Residuen auf. Für diese Annahme wird beobachtet, wie die Werte der Residuen verteilt sind. Es kann mit zwei Methoden getestet werden,

· Ein Histogramm, das eine überlagerte normale Kurve und zeigt

· Die Normal-Probability-Plot-Methode.

Fälle, in denen multiple lineare Regression angewendet wird

Aus Analystensicht ist die multiple lineare Regression ein sehr wichtiger Aspekt. Hier sind einige der Beispiele, wo das Konzept anwendbar sein kann:

ich. Da der Wert der abhängigen Variablen mit den unabhängigen Variablen korreliert, wird die multiple Regression verwendet, um den erwarteten Ertrag einer Ernte bei bestimmten Niederschlagsmengen, Temperaturen und Düngemitteln vorherzusagen.

ii. Die multiple lineare Regressionsanalyse wird auch verwendet, um Trends und zukünftige Werte vorherzusagen. Dies ist besonders nützlich, um den Goldpreis in den nächsten sechs Monaten vorherzusagen.

iii. In einem besonderen Beispiel wird die Beziehung zwischen der von einem UBER-Fahrer zurückgelegten Strecke und dem Alter des Fahrers und der Anzahl der Jahre an Erfahrung des Fahrers herausgenommen. In dieser Regression ist die abhängige Variable die vom UBER-Fahrer zurückgelegte Strecke. Die unabhängigen Variablen sind das Alter des Fahrers und die Anzahl der Jahre Fahrerfahrung.

iv. Ein weiteres Beispiel, bei dem multiple Regressionsanalysen verwendet werden, um die Beziehung zwischen dem GPA einer Klasse von Schülern und der Anzahl der Stunden, die sie lernen, und der Größe der Schüler zu finden. Die abhängige Variable in dieser Regression ist der GPA, und die unabhängigen Variablen sind die Anzahl der Studienstunden und die Größe der Studenten.

v. Mit einer Regressionsanalyse lässt sich der Zusammenhang zwischen dem Gehalt einer Gruppe von Mitarbeitern in einer Organisation und der Anzahl der Jahre der Betriebszugehörigkeit sowie dem Alter der Mitarbeiter ermitteln. Die abhängige Variable für diese Regression ist das Gehalt, die unabhängigen Variablen sind die Erfahrung und das Alter der Mitarbeiter.

Lesen Sie auch: 6 Arten von Regressionsmodellen im maschinellen Lernen, die Sie kennen sollten

Mehrfache lineare Regression in R

Es gibt viele Möglichkeiten, eine multiple lineare Regression auszuführen, sie wird jedoch üblicherweise über Statistiksoftware durchgeführt. Eine der am häufigsten verwendeten Software ist R, die kostenlos, leistungsstark und leicht verfügbar ist. Wir werden zuerst die Schritte zur Durchführung der Regression mit R lernen, gefolgt von einem Beispiel für ein klares Verständnis.

Schritte zum Ausführen einer multiplen Regression in R

1. Datensammlung: Die in der Vorhersage zu verwendenden Daten werden gesammelt.
2. Datenerfassung in R: Erfassen der Daten mithilfe des Codes und Importieren einer CSV-Datei
3. Überprüfung der Datenlinearität mit R: Es ist darauf zu achten, dass zwischen der abhängigen und der unabhängigen Variablen ein linearer Zusammenhang besteht. Dies kann mit Streudiagrammen oder dem Code in R erfolgen
4. Anwenden der multiplen linearen Regression in R: Verwenden von Code zum Anwenden einer multiplen linearen Regression in R , um einen Satz von Koeffizienten zu erhalten.
5. Vorhersagen mit R: Am Ende wird ein prognostizierter Wert ermittelt.

Multiple Regression-Implementierung in R

Wir werden verstehen, wie R implementiert wird, wenn eine Umfrage an einer bestimmten Anzahl von Orten von den Forschern des öffentlichen Gesundheitswesens durchgeführt wird, um Daten über die Bevölkerung zu sammeln, die raucht, zur Arbeit fährt und Menschen mit Herzerkrankungen.

Schritt-für-Schritt-Anleitung für die multiple lineare Regression in R:

ich. Laden Sie das Dataset heart.data und führen Sie den folgenden Code aus

lm<-lm(heart.disease ~ Radfahren + Rauchen, data = heart.data)

Das Datensatz-Herz. Data berechnet den Effekt der unabhängigen Variablen Radfahren und Rauchen auf die abhängige Variable Herzkrankheit unter Verwendung von „lm()“ (der Gleichung für das lineare Modell).

ii. Ergebnisse interpretieren

Verwenden Sie die Funktion summary(), um die Ergebnisse des Modells anzuzeigen:

Zusammenfassung (heart.disease.lm)

Diese Funktion fügt die wichtigsten aus dem linearen Modell erhaltenen Parameter in eine Tabelle ein, die wie folgt aussieht:

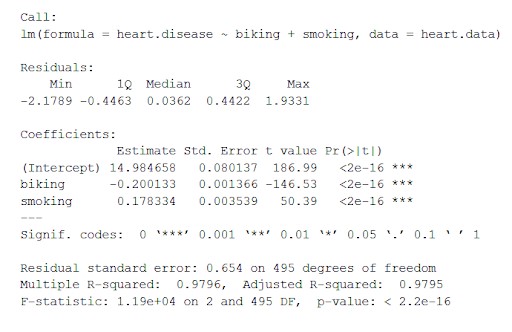
Aus dieser Tabelle können wir ableiten:

• Die Formel von 'Call',
• Die Residuen des Modells („Residuen“). Wenn die Residuen grob um Null zentriert sind und auf beiden Seiten eine ähnliche Streuung aufweisen (Median 0,03 und Min. und Max. -2 und 2), passt das Modell zu den Annahmen der Heteroskedastizität.
• Die Regressionskoeffizienten des Modells („Koeffizienten“).

Zeile 1 der Koeffiziententabelle (Achsenabschnitt): Dies ist der y-Achsenabschnitt der Regressionsgleichung und wird verwendet, um den geschätzten Achsenabschnitt zu kennen, um die Regressionsgleichung einzusetzen und die abhängigen Variablenwerte vorherzusagen.

Herzkrankheit = 15 + (-0,2*Radfahren) + (0,178*Rauchen) ± z

Einige Begriffe im Zusammenhang mit multipler Regression

ich. Schätzspalte : Dies ist der geschätzte Effekt und wird auch als Regressionskoeffizient oder r2-Wert bezeichnet. Die Schätzungen besagen, dass mit jedem Prozent mehr Radfahren zur Arbeit Herzkrankheiten um 0,2 Prozent zurückgehen und mit jedem Prozent mehr Rauchen Herzkrankheiten um 0,17 Prozent.

ii. Std.error : Zeigt den Standardfehler an der Schätzung. Dies ist eine Zahl, die Abweichungen um die Schätzungen des Regressionskoeffizienten herum anzeigt.

iii. t Wert : Zeigt die Teststatistik an . Es ist ein t -Wert aus einem zweiseitigen t-Test .

iv. Pr( > | t | ) : Es ist der p -Wert , der die Wahrscheinlichkeit des Auftretens des t -Werts angibt.

Berichterstattung über die Ergebnisse

Wir sollten den geschätzten Effekt, den Standardschätzungsfehler und den p -Wert einbeziehen.

Im obigen Beispiel wurde festgestellt, dass die signifikanten Beziehungen zwischen der Häufigkeit des Radfahrens zur Arbeit und Herzerkrankungen und der Häufigkeit von Rauchen und Herzerkrankungen p < 0,001 sind.

Die Häufigkeit von Herzerkrankungen wird um 0,2 % (oder ± 0,0014) pro 1 % mehr Radfahren verringert. Die Häufigkeit von Herzerkrankungen erhöht sich um 0,178 % (oder ± 0,0035) pro 1 % Zunahme des Rauchens.

Grafische Darstellung der Ergebnisse

Die Auswirkungen mehrerer unabhängiger Variablen auf die abhängige Variable können in einem Diagramm dargestellt werden. Dabei kann nur eine unabhängige Variable auf der x-Achse aufgetragen werden.

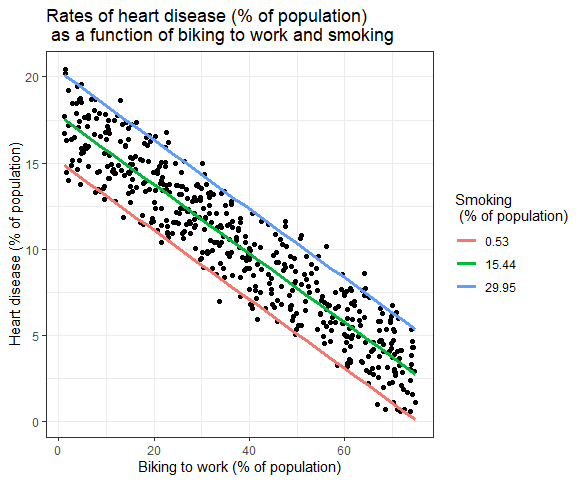
Mehrfache lineare Regression: Grafische Darstellung

Hier sind die prognostizierten Werte der abhängigen Variablen (Herzkrankheit) über den beobachteten Werten für den Prozentsatz der Personen, die mit dem Fahrrad zur Arbeit fahren, aufgetragen.

Für die Auswirkung des Rauchens auf die unabhängige Variable werden die vorhergesagten Werte berechnet, wobei das Rauchen bei den minimalen, mittleren und maximalen Raucherraten konstant gehalten wird.

Lesen Sie auch: Lineare Regression vs. Logistische Regression: Unterschied zwischen linearer Regression und logistischer Regression

Letzte Worte

Dies markiert das Ende dieses Blogbeitrags. Wir haben uns nach besten Kräften bemüht, Ihnen das Konzept der multiplen linearen Regression zu erklären und wie die multiple Regression in R implementiert wird, um die Vorhersageanalyse zu erleichtern.

Wenn Sie Ihre Data-Science-Reise vorantreiben und mehr Konzepte von R und vielen anderen Sprachen lernen möchten, um Ihre Karriere zu stärken, treten Sie upGrad bei . Wir bieten das Advanced Certification Program in Data Science an , das speziell für Berufstätige entwickelt wurde und über 300 Lernstunden mit kontinuierlicher Betreuung umfasst.