Wielokrotna regresja liniowa w R [z wykresami i przykładami]

Jako naukowiec zajmujący się danymi często jesteś proszony o wykonanie analizy predykcyjnej w wielu projektach. Analiza to statystyczne podejście do ustalenia związku między zmienną zależną a zestawem zmiennych niezależnych. Całą tę koncepcję można określić jako regresję liniową, która zasadniczo dzieli się na dwa typy: prostą i wielokrotną regresję liniową.

R jest jednym z najważniejszych języków w zakresie nauki o danych i analityki, podobnie jak wielokrotna regresja liniowa w R ma wartość. Opisuje scenariusz, w którym pojedyncza zmienna odpowiedzi Y zależy liniowo od wielu zmiennych predykcyjnych.

Co to jest regresja liniowa?

Modele regresji liniowej służą do pokazywania lub przewidywania związku między a zmienna zależna i niezależna. Gdy w analizie regresji używane są dwie lub więcej zmiennych niezależnych, model nie jest po prostu liniowy, ale jest modelem regresji wielorakiej.

Prosta regresja liniowa służy do przewidywania wartości jednej zmiennej przy użyciu innej zmiennej. Linia prosta reprezentuje związek między dwiema zmiennymi z regresją liniową.

Istnieje liniowa zależność między zmienną zależną a co najmniej dwiema zmiennymi niezależnymi w regresji wielokrotnej. Zależność może być również nieliniowa, a zmienne zależne i niezależne nie będą przebiegać wzdłuż linii prostej.

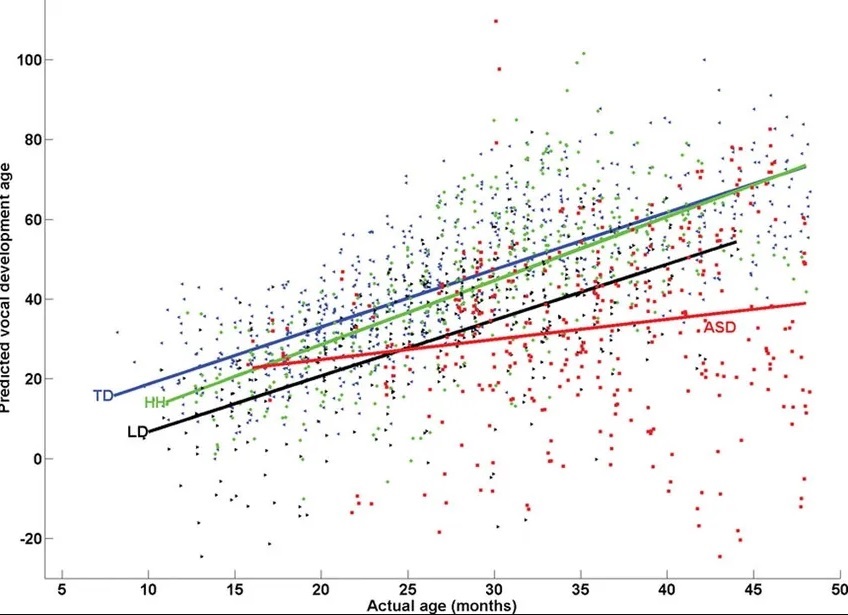
Obrazowe przedstawienie przewidywań modelu regresji liniowej wielokrotnej

Regresja liniowa i nieliniowa służą do śledzenia odpowiedzi przy użyciu co najmniej dwóch zmiennych. Regresja nieliniowa jest tworzona na podstawie założeń opartych na próbach i błędach i jest stosunkowo trudna do wykonania.

Co to jest wielokrotna regresja liniowa?

Wielokrotna regresja liniowa to technika analizy statystycznej używana do przewidywania wyniku zmiennej na podstawie dwóch lub więcej zmiennych. Jest to rozszerzenie regresji liniowej, znanej również jako regresja wielokrotna. Zmienna do przewidzenia jest zmienną zależną, a zmienne używane do przewidywania wartości zmiennej zależnej są znane jako zmienne niezależne lub objaśniające.

Wielokrotna regresja liniowa umożliwia analitykom określenie zmienności modelu i względnego wkładu każdej zmiennej niezależnej. Regresja wielokrotna jest dwojakiego rodzaju, regresja liniowa i nieliniowa.

Formuła regresji wielokrotnej

Regresja wielokrotna z trzema zmiennymi predykcyjnymi (x) zmienna predykcyjna y jest wyrażona jako następujące równanie:

y = z0 + z1*x1 + z2*x2 + z3*x3

Wartości „z” reprezentują wagi regresji i są współczynnikami beta . Są to powiązania między zmienną predykcyjną a wynikiem.

• yi jest zmienną zależną lub przewidywaną
• z0 to punkt przecięcia z osią y, tj. wartość y, gdy x1 i x2 wynoszą 0
• z1 i z2 są współczynnikami regresji reprezentującymi zmianę y związaną odpowiednio ze zmianą o jedną jednostkę w x1 i x2 .

Założenia wielorakiej regresji liniowej

Znaliśmy krótki opis regresji wielokrotnej i podstawową formułę. Istnieją jednak pewne założenia, na których opiera się wielokrotna regresja liniowa, jak opisano poniżej:

i. Związek między zmiennymi zależnymi i niezależnymi

Zmienna zależna jest powiązana liniowo z każdą zmienną niezależną. Aby sprawdzić zależności liniowe, tworzony jest wykres rozrzutu, który jest obserwowany pod kątem liniowości. Jeśli zależność wykresu rozrzutu jest nieliniowa, przeprowadzana jest regresja nieliniowa lub dane są przesyłane za pomocą oprogramowania statystycznego.

ii. Zmienne niezależne nie są zbytnio skorelowane

Dane nie powinny wykazywać współliniowości, co ma miejsce w przypadku, gdy zmienne niezależne są ze sobą silnie skorelowane. Spowoduje to problemy z pobieraniem określonej zmiennej przyczyniającej się do wariancji zmiennej zależnej.

iii. Wariancja rezydualna jest stała

Wielokrotna regresja liniowa zakłada, że ​​błąd pozostałych zmiennych jest podobny w każdym punkcie modelu liniowego. Nazywa się to homoskedastycznością. Po wykonaniu analizy danych, standardowe reszty względem przewidywanych wartości są wykreślane w celu określenia, czy punkty są odpowiednio rozłożone na wartości zmiennych niezależnych.

iv. Obserwacja Niezależność

Obserwacje powinny dotyczyć siebie nawzajem, a wartości rezydualne powinny być niezależne. Najlepiej sprawdza się w tym przypadku statystyka Durbina Watsona.

Metoda pokazuje wartości od 0 do 4, gdzie wartość od 0 do 2 pokazuje pozytywną autokorelację, a od 2 do 4 pokazuje negatywną autokorelację. Punkt środkowy o wartości 2 wskazuje na brak autokorelacji.

v. Wielowymiarowa normalność

Wielowymiarowa normalność występuje w przypadku reszt o rozkładzie normalnym. Dla tego założenia obserwuje się rozkład wartości reszt. Można go przetestować dwoma metodami,

· Histogram przedstawiający nałożoną krzywą normalną i

· Metoda wykresu normalnego prawdopodobieństwa.

Przypadki, w których zastosowano wielokrotną regresję liniową

Wielokrotna regresja liniowa jest bardzo ważnym aspektem z punktu widzenia analityka. Oto kilka przykładów, w których koncepcja może mieć zastosowanie:

i. Ponieważ wartość zmiennej zależnej jest skorelowana ze zmiennymi niezależnymi, regresja wielokrotna jest używana do przewidywania oczekiwanych plonów uprawy przy określonych opadach, temperaturze i poziomie nawozu.

ii. Analiza wielokrotnej regresji liniowej jest również wykorzystywana do przewidywania trendów i przyszłych wartości. Jest to szczególnie przydatne do przewidywania ceny złota za sześć miesięcy od teraz.

iii. W szczególnym przykładzie, w którym bierze się pod uwagę zależność między odległością przebytą przez kierowcę UBER a wiekiem kierowcy i liczbą lat doświadczenia kierowcy. W tej regresji zmienną zależną jest dystans pokonany przez kierowcę UBER. Zmiennymi niezależnymi są wiek kierowcy oraz ilość lat doświadczenia w prowadzeniu pojazdu.

iv. Inny przykład, w którym analiza regresji wielokrotnych jest wykorzystywana do znalezienia związku między GPA klasy uczniów a liczbą godzin nauki i wzrostem uczniów. Zmienną zależną w tej regresji jest GPA, a zmiennymi niezależnymi liczba godzin nauki i wzrost studentów.

v. Stosunek wynagrodzenia grupy pracowników w organizacji do liczby lat eksorganizacji wieku pracowników można określić za pomocą analizy regresji. Zmienną zależną dla tej regresji jest wynagrodzenie, a zmiennymi niezależnymi doświadczenie i wiek pracowników.

Przeczytaj także: 6 typów modeli regresji w uczeniu maszynowym, o których powinieneś wiedzieć

Wielokrotna regresja liniowa w R

Istnieje wiele sposobów na wykonanie wielokrotnej regresji liniowej, ale zwykle odbywa się to za pomocą oprogramowania statystycznego. Jednym z najczęściej używanych programów jest R, który jest darmowy, wydajny i łatwo dostępny. Najpierw nauczymy się kroków do wykonania regresji z R, a następnie na przykładzie jasnego zrozumienia.

Kroki do wykonania wielokrotnej regresji w R

1. Zbieranie danych: Zbierane są dane do wykorzystania w prognozie.
2. Przechwytywanie danych w R: Przechwytywanie danych za pomocą kodu i importowanie pliku CSV
3. Sprawdzanie liniowości danych za pomocą R: Ważne jest, aby upewnić się, że istnieje liniowa zależność między zmienną zależną i niezależną. Można to zrobić za pomocą wykresów punktowych lub kodu w R
4. Stosowanie wielokrotnej regresji liniowej w R: Używanie kodu do zastosowania wielokrotnej regresji liniowej w R w celu uzyskania zestawu współczynników.
5. Dokonywanie prognozy za pomocą R: Przewidywana wartość jest określana na końcu.

Implementacja regresji wielokrotnej w R

Zrozumiemy, w jaki sposób R jest wdrażane, gdy w określonej liczbie miejsc przeprowadzimy ankietę przez naukowców zajmujących się zdrowiem publicznym, aby zebrać dane na temat populacji palących, podróżujących do pracy i osób z chorobami serca.

Przewodnik krok po kroku dla wielokrotnej regresji liniowej w R:

i. Załaduj zestaw danych heart.data i uruchom następujący kod

lm<-lm(serce.choroba ~ jazda na rowerze + palenie, dane = serce.dane)

Serce zestawu danych. Dane obliczają wpływ zmiennych niezależnych jazdy na rowerze i palenia na zmienną zależną choroby serca za pomocą „lm()” (równanie modelu liniowego).

ii. Interpretowanie wyników

użyj funkcji summary(), aby wyświetlić wyniki modelu:

podsumowanie(serce.choroba.lm)

Funkcja ta umieszcza najważniejsze parametry uzyskane z modelu liniowego w tabeli, która wygląda jak poniżej:

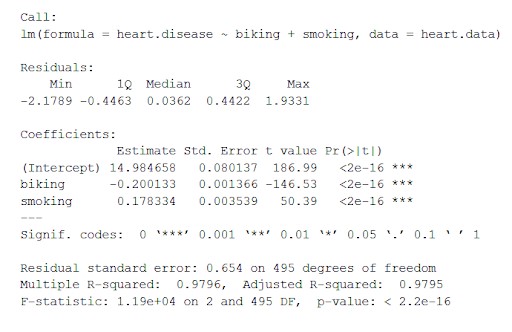
Z tej tabeli możemy wywnioskować:

• Formuła „Zadzwoń”,
• Reszty modelu („Residuals”). Jeśli reszty są z grubsza wyśrodkowane wokół zera i mają podobny rozrzut po obu stronach (mediana 0,03 oraz min i max -2 i 2), wówczas model pasuje do założeń heteroskedastyczności.
• Współczynniki regresji modelu („Współczynniki”).

Wiersz 1 tabeli współczynników (punkt przecięcia): jest to punkt przecięcia y równania regresji i służy do poznania szacowanego punktu przecięcia w celu wprowadzenia równania regresji i przewidzenia wartości zmiennych zależnych.

choroba serca = 15 + (-0,2*jazda na rowerze) + (0,178*palenie) ± e

Niektóre terminy związane z regresją wielokrotną

i. Kolumna oszacowania : jest to szacowany efekt i jest również nazywany współczynnikiem regresji lub wartością r2. Szacunki mówią, że z każdym 1% wzrostem liczby osób jeżdżących na rowerze do pracy jest związany z tym 0,2% spadek chorób serca, a każdy procent wzrostu palenia powoduje wzrost liczby chorób serca o 0,17%.

ii. Std.error : Wyświetla standardowy błąd oszacowania. Jest to liczba, która pokazuje zmienność oszacowań współczynnika regresji.

iii. t Wartość : wyświetla statystykę testu . Jest to wartość t z dwustronnego testu t .

iv. Pr( > | t | ) : Jest to wartość p , która pokazuje prawdopodobieństwo wystąpienia wartości t .

Raportowanie wyników

Powinniśmy uwzględnić oszacowany efekt, standardowy błąd oszacowania i wartość p .

W powyższym przykładzie stwierdzono, że istotne zależności między częstością dojeżdżania do pracy rowerem a chorobami serca a częstością palenia i chorobami serca wynoszą p < 0,001.

Częstość występowania chorób serca zmniejsza się o 0,2% (lub ± 0,0014) na każdy 1% wzrostu na rowerze. Częstość występowania chorób serca wzrasta o 0,178% (lub ± 0,0035) na każdy 1% wzrostu palenia.

Graficzne przedstawienie ustaleń

Wpływ wielu zmiennych niezależnych na zmienną zależną można przedstawić na wykresie. W tym przypadku tylko jedna niezależna zmienna może być wykreślona na osi x.

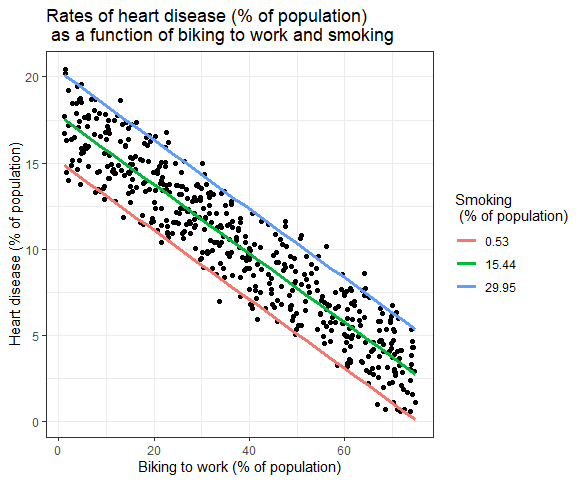
Wielokrotna regresja liniowa: reprezentacja graficzna

W tym miejscu wykreślono przewidywane wartości zmiennej zależnej (choroba serca) w obserwowanych wartościach odsetka osób jeżdżących rowerem do pracy.

Dla wpływu palenia na zmienną niezależną oblicza się przewidywane wartości, utrzymując stałe palenie na minimalnym, średnim i maksymalnym poziomie palenia.

Przeczytaj także: Regresja liniowa vs. Regresja logistyczna: różnica między regresją liniową a regresją logistyczną

Ostatnie słowa

To oznacza koniec tego wpisu na blogu. Dołożyliśmy wszelkich starań, aby wyjaśnić Ci koncepcję wielokrotnej regresji liniowej oraz sposób implementacji wielokrotnej regresji w R w celu ułatwienia analizy predykcyjnej.

Jeśli chcesz wesprzeć swoją podróż naukową o danych i dowiedzieć się więcej pojęć języka R i wielu innych języków, aby wzmocnić swoją karierę, dołącz do upGrad . Oferujemy Advanced Certification Program in Data Science , który jest specjalnie zaprojektowany dla pracujących profesjonalistów i obejmuje ponad 300 godzin nauki z ciągłym mentoringiem.