數據結構中的表達式解析：符號類型、關聯性和優先級

解析是分析一串符號的過程，這些符號以符合形式語法的自然或計算機語言表達。 數據結構中的表達式解析意味著對算術和邏輯表達式的評估。 首先，讓我們看看算術表達式是如何寫的：

• 9+9
• CB

表達式可以用可以充當運算符或括號的常量、變量和符號來編寫。 所有這些表達式都需要遵循一組特定的規則。 根據這個規則，表達式的解析是基於語法來完成的。

算術表達式以 Notation 的形式表示。 現在，有三種方法可以在算術中編寫表達式：

• 中綴符號
• 前綴（波蘭語）表示法
• 後綴（反向波蘭）表示法

但是，在編寫表達式時，所需表達式的輸出保持不變。 在開始介紹 Notation 的類型之前，讓我們看看 Associativity 和 Precedence在數據結構中的表達式解析中是什麼。

如果您是初學者並且有興趣了解有關數據科學的更多信息，請查看我們來自頂尖大學的數據科學課程。

閱讀：數據結構中的圖

關聯性

在開始之前，您需要知道什麼是關聯性屬性； 它為您提供了在表達式中重新排列括號以提供有效證明的規則。 這意味著括號的重新排列需要給出與父方程相同的值。 它提供了替換運算符的有效規則。

在包含兩個或多個運算符的表達式中，除非操作數序列不互換，否則執行的操作無關緊要。 如果表達式是使用方括號和中綴編寫的，則更改位置不會更改值。

因為在印歐語言中，表達式是從左到右讀取的，所以大多數中綴運算符都是左結合的； 運算符的計算優先級相同。 權力上升是考慮中綴運算符時使用的規則。 前綴運算符通常是右關聯的，而後綴運算符是左關聯的。

在某些語言中，運算符和操作數被賦予相同的值，其中不考慮關聯性使該語言序列顯式化。 雖然在某些語言中，運算符是非關聯的，但這使得使用括號必須使用複雜的表達式，這增加了程序員的複雜性。

數據結構中的優先級

優先順序是指運算符在表達式語句中需要遵循的順序。 這通常在使用中綴表示法時使用。

在<operator> <operand> <operator> 操作數介於兩個運算符之間的情況下，分配運算符的優先級是相當棘手的。 因此，遵循算子優先規則進行計算。 例如，這裡，乘法的優先級較高，然後進行加法運算。

• 最常見但不那麼明顯的規則是乘法和除法運算必須在加法和減法之前執行。 通常，它們以相同的方式收集，因此為所有操作員提供同等重要性。
• 以邏輯格式考慮此操作，可以在“and”和“or”中看到變化。 許多語言提供同等的重要性，其中“或”操作具有更高的優先級。 一些語言考慮乘法或“&”、“&”加法“或”相等的優先級，其中大多數語言提供具有最高優先級的算術運算。
• 重載是由於沒有正確分配優先級引起的。 許多語言提供比向量代數表達式更高的否定（真/假）優先級，而有些語言提供相等的優先級。

另請閱讀：數據結構項目理念

符號類型

現在讓我們來了解一下操作符的位置如何決定 Notation 的類型。

1. 中綴符號

在中綴表示法中，運算符用於操作數之間。 在閱讀表達式時，中綴表示法對人類來說非常容易。 但是當涉及到計算機算法時，處理中綴參數是相當耗費時間和空間的。 例如：p + q

<操作數> <操作數> <操作數>

中綴表示法需要額外的信息來執行評估； 使用運算符Associativity 、 例如：p * ( q + r ) / s

• 關聯性規則表明表達式需要從左到右執行，這樣 p 的乘法就在 q 的除法之前完成。
• 類似地，優先級規則建議在完成加減運算之前執行乘法和除法運算。

2.前綴表示法

這裡先寫操作符，然後是操作數。 它也被稱為波蘭符號。 例如 +pq

<操作符> <操作數> <操作數>

例如： p * ( q + r ) / s

評估需要從左到右進行，括號不會改變或改變方程模式。 這裡，加法需要在乘法之前完成，因為位置“+”在“*”的左邊。

在這裡，每個運算符都對緊鄰它們左側的值執行操作。 例如，上面的“+”使用“q”和“r”。 我們可以總結括號來明確這一點：

((p (qr +) *) s /)

因此，“( )”考慮並使用緊接在“p”之前的兩個值，以及 + 的結果。 同樣，“/”使用乘法表達式和“s”的結果。

3. 後綴符號

後綴符號，主要是操作數，被寫入，然後是一個運算符。 它也被稱為逆波蘭表示法，例如 pq+

<操作數> <操作數> <操作數>

至於後綴，與表達式的前綴操作一樣是從左到右，不需要“( )”。 在這裡，運算符對右邊最接近的兩個值執行。 在下面的示例中，不必要地添加了括號，以表明對評估沒有影響。

(/ (* p (+ qr) ) s)

這裡“算子評估是從左到右”的操作值在他們的右邊，如果值本身涉及計算，那麼評估的順序就會發生變化。 以上面列出的示例為例，“/”是左側的主要運算符。

它一直等到乘法運算完成。 並且首先需要在除法計算開始之前進行乘法運算（從上面的例子可以看出，在乘法運算之前需要完成加法運算）。

因為 Postfix Notation 運算符使用右邊的值； 當我們向左移動時，任何涉及計算的值都將計算已經完成。 因此，我們可以得出結論，表達式計算與前綴運算符操作不同。

為了突出所有三個符號，操作數以相同的順序出現，並且需要移動運算符以在計算過程中提供正確的含義。 在考慮不對稱運算符“-”和“/”時需要特別考慮這一點，以明確 pq 永遠是 qr，除非它們具有相同的值； 這些值相當於“pq -”或“- pq”

P+q ≡ +pq ≡ pq+

例如：

中綴- p * q + r / s

前綴 – pq * rs / +

後修復 - + * pq / rs

首先，要執行運算，將 p 和 q 相乘，然後將 r 除以 s，最後將結果相加。

下表簡要介紹了三種符號之間的關係，

中綴符號	波蘭符號	反向波蘭符號
p+q	+pq	q+
(p+q)*r	+*pq	pqr+*
p*(q+r)	*p+qr	pqr*++
p÷q+r÷s	+÷pq÷rs	pq÷rs÷+
(pq)*(rs)	*-pq-rs	pq-rs-*

符號之間的轉換

*為了提供清晰的見解，在表達式中添加了括號，

中綴	後綴	字首
( (p * q) + (r / s) )	( (pq *) (rs /) +)	(+ (* pq) (/ rs) )
((p * (q + r) ) / s)	( (p (qr +) *) s /)	(/ (* p (+ qr) ) s)
(p * (q + (r / s) ) )	(p (q (rs /) +) *)	(* p (+ q (/ rs) ) )

• 您可以通過括號中的運算符直接開始轉換括號形式，例如 (m + n) 或 (mn +) 或 (+ mn)。 現在通過刪除不需要的括號在所有運算符中重複此操作。
• 現在使用上面顯示的這個技巧來轉換和解析樹 - 每個節點的等效解析樹是：

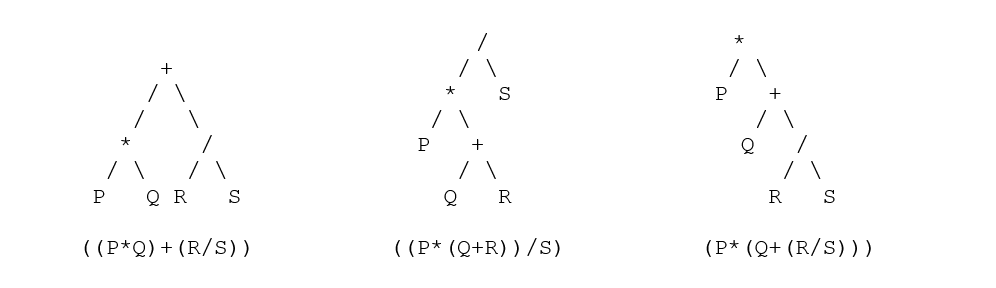
結帳： Python中的數據結構和算法

結論

數據結構中的表達式解析，算術表達式中的中綴、後綴和前綴表示法是完全不同的，但具有相同的表達式編寫方式。 這些知識對於編寫程序至關重要。

在計算機編程語言中，表達式是從字符串中考慮和解析的。 關聯性和優先級規則在不同語言中發生了很大變化。

為什麼選擇 upGrad 的數據科學課程？

數據科學是計算機科學中蓬勃發展的領域之一。 公司需要具有良好基礎知識的程序員，這是編程的基礎，而與編碼語言無關。

upGrad 專注於提供富有洞察力和信息豐富的課程，涵蓋成為數據科學家的所有基本需求。 upGrad 為期 12 個月的數據科學執行 PG 計劃。 由 IIIT Bangalore 提供，是印度第一個 NASSCOM 認證課程，由數據科學行業專家提供 1:1 個性化指導，涵蓋所有基本的編程語言、工具和庫。 它為您開始高薪數據科學工作提供了最佳基礎。

什麼是數據結構？

數據結構用於組織內存中的數據。 有幾種方法可以在內存中排列數據，包括數組、列表、堆棧、隊列等。 數據結構不是像 C、C++ 或 Java 那樣的編程語言。 相反，它是一組用於以任何編程語言在內存中排列數據的技術。 數據結構是一種有效組織、處理和存儲數據的方法。 在數據結構的幫助下，可以簡單地遍歷數據項。 這對於提高程序的速度至關重要，因為程序的主要工作是盡可能快地保存和檢索用戶的數據。

數據解析的實際用途是什麼？

將數據從一種格式轉換為另一種格式的過程稱為數據解析。 它們廣泛用於編譯器中，用於解析計算機代碼和生成機器代碼。 將數據從一種格式轉換為另一種格式的過程稱為數據解析。 因為我們收到的原始 HTML 很難理解，所以解析器經常用於在線抓取。 我們要求將數據轉換為人類可讀的格式。 這可能意味著使用 HTML 字符串或表格構建報告以提供最相關的信息。

關聯性和優先級如何幫助數據結構化？

表達式的求值順序由運算符的兩個屬性決定：優先級和關聯性。 優先級有助於確定表達式中的術語應如何分組以及如何評估表達式。 因為大多數表達式使用 BODMAS 框架，某些運算符優先於其他運算符。 當兩個運算符在表達式中具有相同的優先級時，將應用關聯規則。 根據編譯器的偏好，關聯性可能是從左到右或從右到左。