Regressão linear múltipla em R [com gráficos e exemplos]

Como cientista de dados, você é frequentemente solicitado a fazer análises preditivas em muitos projetos. Uma análise é uma abordagem estatística para estabelecer uma relação entre uma variável dependente com um conjunto de variáveis ​​independentes. Todo esse conceito pode ser denominado como uma regressão linear, que é basicamente de dois tipos: regressão linear simples e múltipla.

R é uma das linguagens mais importantes em termos de ciência e análise de dados, assim como a regressão linear múltipla em R mantém valor. Ele descreve o cenário em que uma única variável de resposta Y depende linearmente de várias variáveis ​​preditoras.

O que é uma regressão linear?

Modelos de regressão linear são usados ​​para mostrar ou prever a relação entre um dependente e uma variável independente. Quando há duas ou mais variáveis ​​independentes usadas na análise de regressão, o modelo não é simplesmente linear, mas um modelo de regressão múltipla.

A regressão linear simples é usada para prever o valor de uma variável usando outra variável. Uma linha reta representa a relação entre as duas variáveis ​​com regressão linear.

Existe uma relação linear entre uma variável dependente com duas ou mais variáveis ​​independentes na regressão múltipla. A relação também pode ser não linear, e as variáveis ​​dependentes e independentes não seguirão uma linha reta.

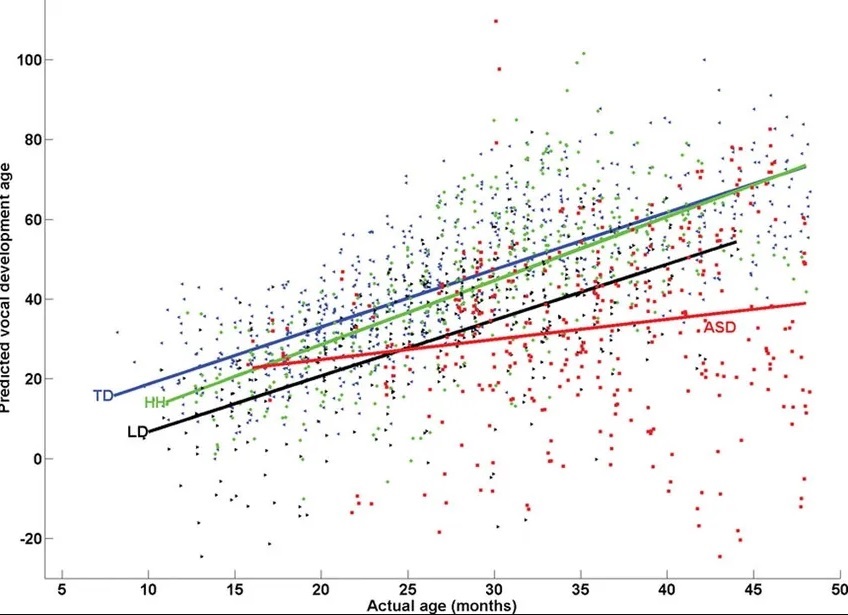
Representação pictórica de previsões de modelos de regressão linear múltipla

A regressão linear e não linear é usada para rastrear uma resposta usando duas ou mais variáveis. A regressão não linear é criada a partir de suposições de tentativa e erro e é comparativamente difícil de executar.

O que é Regressão Linear Múltipla?

A regressão linear múltipla é uma técnica de análise estatística usada para prever o resultado de uma variável com base em duas ou mais variáveis. É uma extensão da regressão linear e também conhecida como regressão múltipla. A variável a ser prevista é a variável dependente, e as variáveis ​​usadas para prever o valor da variável dependente são conhecidas como variáveis ​​independentes ou explicativas.

A regressão linear múltipla permite que os analistas determinem a variação do modelo e a contribuição relativa de cada variável independente. A regressão múltipla é de dois tipos, regressão linear e não linear.

Fórmula de regressão múltipla

A regressão múltipla com três variáveis ​​de previsão (x) variável de previsão y é expressa como a seguinte equação:

y = z0 + z1*x1 + z2*x2 + z3*x3

Os valores “z” representam os pesos da regressão e são os coeficientes beta . São a associação entre a variável preditora e o desfecho.

• yi é uma variável dependente ou predita
• z0 é a interceptação de y, ou seja, o valor de y quando x1 e x2 são 0
• z1 e z2 são os coeficientes de regressão que representam a mudança em y relacionada a uma mudança de uma unidade em x1 e x2 , respectivamente.

Suposições de Regressão Linear Múltipla

Conhecemos o resumo sobre regressão múltipla e a fórmula básica. No entanto, existem algumas suposições nas quais a regressão linear múltipla é baseada detalhada como abaixo:

eu. Relação entre variáveis ​​dependentes e independentes

A variável dependente relaciona-se linearmente com cada variável independente. Para verificar as relações lineares, um gráfico de dispersão é criado e observado quanto à linearidade. Se a relação do gráfico de dispersão não for linear, uma regressão não linear será executada ou os dados serão transferidos usando um software estatístico.

ii. As variáveis ​​independentes não são muito correlacionadas

Os dados não devem apresentar multicolinearidade, o que acontece caso as variáveis ​​independentes sejam altamente correlacionadas entre si. Isso criará problemas na busca da variável específica que contribui para a variação na variável dependente.

iii. A Variação Residual é Constante

A regressão linear múltipla assume que o erro das demais variáveis ​​é semelhante em cada ponto do modelo linear. Isso é conhecido como homocedasticidade. Quando a análise dos dados é feita, os resíduos padrão em relação aos valores previstos são plotados para determinar se os pontos estão distribuídos adequadamente entre os valores das variáveis ​​independentes.

4. Independência de Observação

As observações devem ser umas das outras e os valores residuais devem ser independentes. A estatística Durbin Watson funciona melhor para isso.

O método apresenta valores de 0 a 4, onde um valor entre 0 e 2 indica autocorrelação positiva e de 2 a 4, autocorrelação negativa. O ponto médio, um valor de 2, mostra que não há autocorrelação.

v. Normalidade Multivariada

A normalidade multivariada acontece com resíduos normalmente distribuídos. Para esta suposição, observa-se como os valores dos resíduos são distribuídos. Pode ser testado usando dois métodos,

· Um histograma mostrando uma curva normal sobreposta e

· O método do gráfico de probabilidade normal.

Instâncias em que a regressão linear múltipla é aplicada

A regressão linear múltipla é um aspecto muito importante do ponto de vista de um analista. Aqui estão alguns dos exemplos em que o conceito pode ser aplicável:

eu. Como o valor da variável dependente está correlacionado com as variáveis ​​independentes, a regressão múltipla é usada para prever o rendimento esperado de uma cultura em determinada precipitação, temperatura e nível de fertilizante.

ii. A análise de regressão linear múltipla também é usada para prever tendências e valores futuros. Isso é particularmente útil para prever o preço do ouro nos próximos seis meses.

iii. Em um exemplo particular onde é retirada a relação entre a distância percorrida por um motorista UBER e a idade do motorista e o número de anos de experiência do motorista. Nesta regressão, a variável dependente é o distância percorrida pelo motorista UBER. As variáveis ​​independentes são a idade do condutor e o número de anos de experiência na condução.

4. Outro exemplo em que a análise de regressões múltiplas é usada para encontrar a relação entre o GPA de uma turma de alunos e o número de horas que eles estudam e a altura dos alunos. A variável dependente nesta regressão é o GPA, e as variáveis ​​independentes são o número de horas de estudo e a altura dos alunos.

v. A relação entre o salário de um grupo de empregados de uma organização e o número de anos de experiência na organização e a idade dos empregados pode ser determinada com uma análise de regressão. A variável dependente para esta regressão é o salário, e as variáveis ​​independentes são a experiência e a idade dos funcionários.

Leia também: 6 tipos de modelos de regressão em aprendizado de máquina que você deve conhecer

Regressão Linear Múltipla em R

Há muitas maneiras de executar a regressão linear múltipla, mas geralmente é feita por meio de software estatístico. Um dos softwares mais usados ​​é o R, que é gratuito, poderoso e disponível facilmente. Vamos primeiro aprender os passos para realizar a regressão com R, seguido por um exemplo de um entendimento claro.

Etapas para executar a regressão múltipla em R

1. Coleção de dados: Os dados a serem usados ​​na previsão são coletados.
2. Captura de dados em R: Capturando os dados usando o código e importando um arquivo CSV
3. Verificando a linearidade dos dados com R: É importante certificar-se de que existe uma relação linear entre a variável dependente e a variável independente. Isso pode ser feito usando gráficos de dispersão ou o código em R
4. Aplicando Regressão Linear Múltipla em R: Usando código para aplicar regressão linear múltipla em R para obter um conjunto de coeficientes.
5. Fazendo previsão com R: Um valor previsto é determinado no final.

Implementação de regressão múltipla em R

Vamos entender como o R é implementado quando uma pesquisa é realizada em um determinado número de locais pelos pesquisadores de saúde pública para coletar os dados sobre a população que fuma, que viaja para o trabalho e as pessoas com doenças cardíacas.

Guia passo a passo para regressão linear múltipla em R:

eu. Carregue o conjunto de dados heart.data e execute o seguinte código

lm<-lm(doença do coração ~ andar de bicicleta + fumar, dados = coração.dados)

O coração do conjunto de dados. Os dados calculam o efeito das variáveis ​​independentes andar de bicicleta e fumar na variável dependente doença cardíaca usando 'lm()' (a equação para o modelo linear).

ii. Interpretando resultados

use a função summary() para visualizar os resultados do modelo:

resumo(doença do coração.lm)

Esta função coloca os parâmetros mais importantes obtidos do modelo linear em uma tabela que se parece com a abaixo:

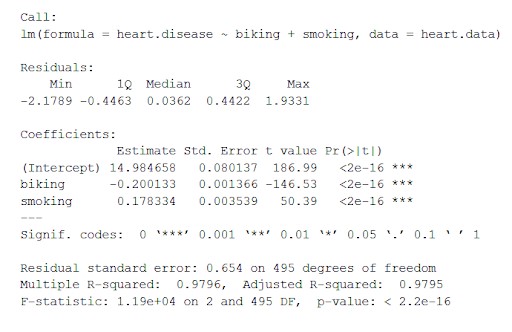
A partir desta tabela podemos inferir:

• A fórmula de 'Chamada',
• Os resíduos do modelo ('Resíduos'). Se os resíduos estão aproximadamente centrados em torno de zero e com dispersão semelhante em ambos os lados (mediana 0,03 e min e max -2 e 2), então o modelo se ajusta às suposições de heterocedasticidade.
• Os coeficientes de regressão do modelo ('Coeficientes').

Linha 1 da tabela de coeficientes (Interceptar): Esta é a interceptação y da equação de regressão e usada para conhecer a interceptação estimada para inserir a equação de regressão e prever os valores das variáveis ​​dependentes.

doença cardíaca = 15 + (-0,2*ciclismo) + (0,178*fumar) ± e

Alguns Termos Relacionados à Regressão Múltipla

eu. Coluna Estimativa : É o efeito estimado e também é chamado de coeficiente de regressão ou valor r2. As estimativas dizem que para cada aumento de 1% no ciclismo para o trabalho há uma diminuição associada de 0,2% nas doenças cardíacas, e para cada aumento percentual no tabagismo há um aumento de 0,17% nas doenças cardíacas.

ii. Std.error : Exibe o erro padrão da estimativa. Este é um número que mostra variação em torno das estimativas do coeficiente de regressão.

iii. t Valor : Exibe a estatística do teste . É um valor t de um teste t bilateral .

4. Pr( > | t | ) : É o valor p que mostra a probabilidade de ocorrência do valor t .

Relatando os Resultados

Devemos incluir o efeito estimado, o erro padrão de estimativa e o valor- p .

No exemplo acima, as relações significativas entre a frequência de ir de bicicleta para o trabalho e doenças cardíacas e a frequência de tabagismo e doenças cardíacas foram p < 0,001.

A frequência de doenças cardíacas diminui em 0,2% (ou ± 0,0014) para cada aumento de 1% no ciclismo. A frequência de doenças cardíacas aumenta em 0,178% (ou ± 0,0035) para cada aumento de 1% no tabagismo.

Representação Gráfica dos Resultados

Os efeitos de múltiplas variáveis ​​independentes na variável dependente podem ser mostrados em um gráfico. Neste, apenas uma variável independente pode ser plotada no eixo x.

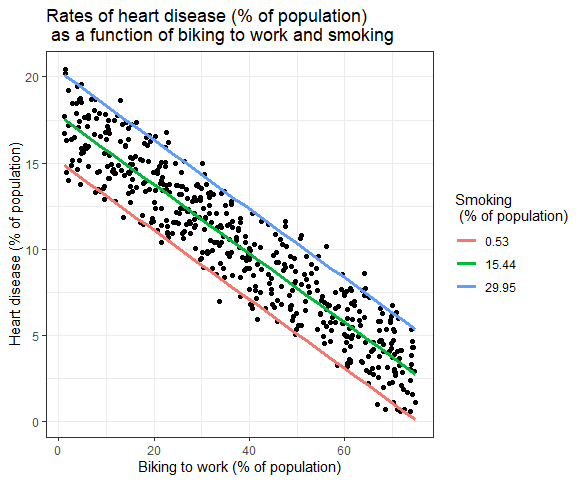
Regressão Linear Múltipla: Representação Gráfica

Aqui, os valores previstos da variável dependente (doença cardíaca) entre os valores observados para a porcentagem de pessoas que vão de bicicleta para o trabalho são plotados.

Para o efeito do tabagismo na variável independente, calculam-se os valores previstos, mantendo-se o tabagismo constante nas taxas mínima, média e máxima de tabagismo.

Leia também: Regressão Linear vs. Regressão Logística: Diferença entre Regressão Linear e Regressão Logística

Palavras finais

Isso marca o fim desta postagem no blog. Tentamos o melhor de nossos esforços para explicar a você o conceito de regressão linear múltipla e como a regressão múltipla em R é implementada para facilitar a análise de previsão.

Se você deseja endossar sua jornada de ciência de dados e aprender mais conceitos de R e muitas outras linguagens para fortalecer sua carreira, junte-se ao upGrad . Oferecemos o Programa de Certificação Avançada em Ciência de Dados , especialmente desenvolvido para profissionais que trabalham e inclui mais de 300 horas de aprendizado com orientação contínua.