Множественная линейная регрессия в R [с графиками и примерами]

Как специалиста по данным, вас часто просят провести прогнозный анализ во многих проектах. Анализ — это статистический подход к установлению взаимосвязи между зависимой переменной и набором независимых переменных. Всю эту концепцию можно назвать линейной регрессией, которая в основном бывает двух типов: простая и множественная линейная регрессия.

R — один из самых важных языков с точки зрения науки о данных и аналитики, поэтому множественная линейная регрессия в R имеет значение. Он описывает сценарий, в котором одна переменная отклика Y линейно зависит от нескольких переменных-предикторов.

Что такое линейная регрессия?

Модели линейной регрессии используются, чтобы показать или предсказать взаимосвязь между зависимая и независимая переменная. Когда в регрессионном анализе используются две или более независимых переменных, модель является не просто линейной, а моделью множественной регрессии.

Простая линейная регрессия используется для прогнозирования значения одной переменной с использованием другой переменной. Прямая линия представляет отношение между двумя переменными с помощью линейной регрессии.

Существует линейная связь между зависимой переменной и двумя или более независимыми переменными в множественной регрессии. Связь также может быть нелинейной, и зависимая и независимая переменные не будут следовать прямой линии.

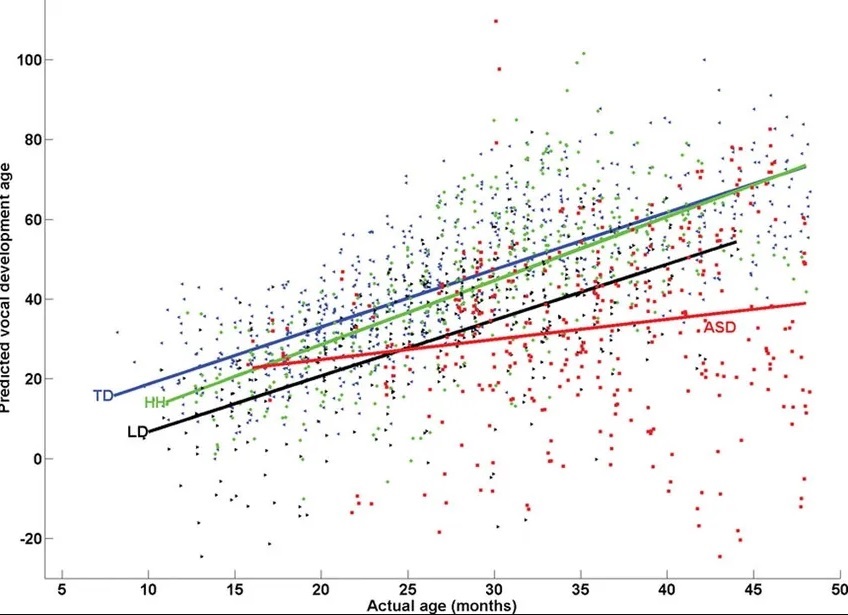
Графическое представление прогнозов модели множественной линейной регрессии

Линейная и нелинейная регрессия используются для отслеживания ответа с использованием двух или более переменных. Нелинейная регрессия создается на основе предположений методом проб и ошибок, и ее сравнительно сложно выполнить.

Что такое множественная линейная регрессия?

Множественная линейная регрессия — это метод статистического анализа, используемый для прогнозирования результата переменной на основе двух или более переменных. Это расширение линейной регрессии, также известное как множественная регрессия. Прогнозируемая переменная является зависимой переменной, а переменные, используемые для прогнозирования значения зависимой переменной, известны как независимые или независимые переменные.

Множественная линейная регрессия позволяет аналитикам определить вариацию модели и относительный вклад каждой независимой переменной. Множественная регрессия бывает двух типов: линейная и нелинейная регрессия.

Формула множественной регрессии

Множественная регрессия с тремя переменными-предикторами (x), предсказывающими переменную y, выражается в виде следующего уравнения:

у = z0 + z1*x1 + z2*x2 + z3*x3

Значения «z» представляют веса регрессии и представляют собой бета-коэффициенты . Они представляют собой связь между предикторной переменной и результатом.

• yi является зависимой или прогнозируемой переменной
• z0 — точка пересечения с осью y, т. е. значение y, когда x1 и x2 равны 0.
• z1 и z2 — коэффициенты регрессии, представляющие изменение y, связанное с изменением x1 и x2 на одну единицу соответственно.

Предположения множественной линейной регрессии

Мы узнали краткую информацию о множественной регрессии и основную формулу. Однако есть некоторые допущения, на которых основана множественная линейная регрессия, подробно описанные ниже:

я. Связь между зависимыми и независимыми переменными

Зависимая переменная линейно связана с каждой независимой переменной. Чтобы проверить линейные отношения, создается диаграмма рассеяния и наблюдается ее линейность. Если зависимость диаграммы рассеяния нелинейна, то выполняется нелинейная регрессия или данные передаются с использованием статистического программного обеспечения.

II. Независимые переменные мало коррелированы

Данные не должны отображать мультиколлинеарность, что происходит в случае, если независимые переменные сильно коррелируют друг с другом. Это создаст проблемы при извлечении конкретной переменной, влияющей на дисперсию зависимой переменной.

III. Остаточная дисперсия постоянна

Множественная линейная регрессия предполагает, что ошибка остальных переменных одинакова в каждой точке линейной модели. Это известно как гомоскедастичность. Когда анализ данных выполнен, стандартные остатки по сравнению с прогнозируемыми значениями строятся на графике, чтобы определить, правильно ли распределены точки по значениям независимых переменных.

IV. Независимость наблюдения

Наблюдения должны быть связаны друг с другом, а остаточные значения должны быть независимыми. Лучше всего для этого подходит статистика Дарбина Уотсона.

Метод показывает значения от 0 до 4, где значение от 0 до 2 показывает положительную автокорреляцию, а от 2 до 4 — отрицательную автокорреляцию. Средняя точка, равная 2, показывает отсутствие автокорреляции.

v. Многомерная нормальность

Многомерная нормальность возникает с нормально распределенными остатками. Для этого предположения наблюдается, как распределяются значения остатков. Его можно проверить двумя способами:

· Гистограмма, показывающая наложенную нормальную кривую и

· Метод нормального вероятностного графика.

Случаи применения множественной линейной регрессии

Множественная линейная регрессия — очень важный аспект с точки зрения аналитика. Вот несколько примеров, где эта концепция может быть применима:

я. Поскольку значение зависимой переменной коррелирует с независимыми переменными, множественная регрессия используется для прогнозирования ожидаемой урожайности культуры при определенных осадках, температуре и уровне удобрений.

II. Множественный линейный регрессионный анализ также используется для прогнозирования тенденций и будущих значений. Это особенно полезно для прогнозирования цены на золото на ближайшие шесть месяцев.

III. В конкретном примере вынесена связь между расстоянием, пройденным водителем UBER, и возрастом водителя, а также количеством лет стажа водителя. В этой регрессии зависимой переменной является расстояние, пройденное водителем UBER. Независимыми переменными являются возраст водителя и стаж вождения.

IV. Другой пример, когда множественный регрессионный анализ используется для нахождения связи между средним баллом класса студентов, количеством часов, которые они учатся, и ростом студентов. Зависимой переменной в этой регрессии является средний балл, а независимыми переменными являются количество учебных часов и рост учащихся.

v. Соотношение между заработной платой группы служащих в организации и количеством лет exporganizationthe возраста служащих может быть определено с анализом регрессии. Зависимой переменной для этой регрессии является заработная плата, а независимыми переменными являются опыт и возраст сотрудников.

Читайте также: 6 типов регрессионных моделей в машинном обучении, о которых вы должны знать

Множественная линейная регрессия в R

Существует множество способов выполнения множественной линейной регрессии, но обычно это делается с помощью статистического программного обеспечения. Одним из наиболее часто используемых программ является R, который является бесплатным, мощным и легко доступным. Сначала мы изучим шаги для выполнения регрессии с R, а затем пример четкого понимания.

Шаги для выполнения множественной регрессии в R

1. Сбор информации: Собираются данные, которые будут использоваться в прогнозе.
2. Сбор данных в R: сбор данных с помощью кода и импорт файла CSV
3. Проверка линейности данных с помощью R: Важно убедиться, что между зависимой и независимой переменной существует линейная зависимость. Это можно сделать с помощью точечных диаграмм или кода на R.
4. Применение множественной линейной регрессии в R: Использование кода для применения множественной линейной регрессии в R для получения набора коэффициентов.
5. Создание прогноза с помощью R: В конце определяется прогнозируемое значение.

Реализация множественной регрессии в R

Мы поймем, как реализуется R, когда исследователи общественного здравоохранения проведут опрос в определенном количестве мест для сбора данных о населении, которое курит, ездит на работу и о людях с сердечными заболеваниями.

Пошаговое руководство по множественной линейной регрессии в R:

я. Загрузите набор данных heart.data и выполните следующий код.

lm<-lm(heart.disease ~ езда на велосипеде + курение, данные = heart.data)

Сердце набора данных. Данные рассчитывают влияние независимых переменных, езда на велосипеде и курение, на зависимую переменную болезнь сердца, используя 'lm()' (уравнение для линейной модели).

II. Интерпретация результатов

используйте функцию summary() для просмотра результатов модели:

резюме(heart.disease.lm)

Эта функция помещает наиболее важные параметры, полученные из линейной модели, в таблицу, которая выглядит следующим образом:

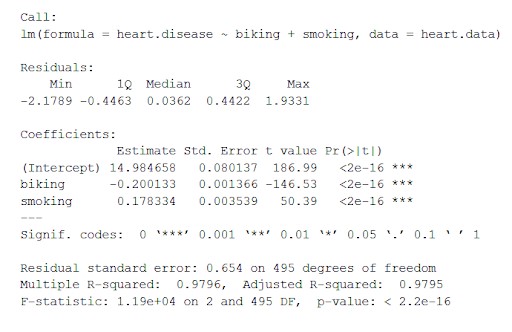
Из этой таблицы мы можем сделать вывод:

• Формула «Вызова»,
• Остатки модели («Остатки»). Если остатки примерно сосредоточены вокруг нуля и с одинаковым разбросом по обеим сторонам (медиана 0,03, а минимум и максимум -2 и 2), то модель соответствует предположениям о гетероскедастичности.
• Коэффициенты регрессии модели («Коэффициенты»).

Строка 1 таблицы коэффициентов (пересечение): это точка пересечения по оси y уравнения регрессии, которая используется, чтобы узнать предполагаемую точку пересечения, чтобы подключить уравнение регрессии и предсказать значения зависимой переменной.

болезнь сердца = 15 + (-0,2*езда на велосипеде) + (0,178*курение) ± e

Некоторые термины, относящиеся к множественной регрессии

я. Столбец оценки : это предполагаемый эффект, который также называется коэффициентом регрессии или значением r2. Оценки говорят о том, что на каждый процент увеличения количества поездок на работу на велосипеде приходится 0,2-процентное снижение частоты сердечных заболеваний, а на каждый процент увеличения количества курящих — 0,17-процентное увеличение числа сердечных заболеваний.

II. Std.error : отображает стандартную ошибку оценки. Это число, которое показывает изменение оценок коэффициента регрессии.

III. t Value : Отображает статистику теста . Это значение t из двустороннего t-теста .

IV. Pr( > | t | ) : это значение p , которое показывает вероятность появления значения t .

Отчет о результатах

Мы должны включить ожидаемый эффект, стандартную ошибку оценки и p - значение.

В приведенном выше примере было обнаружено, что значимая взаимосвязь между частотой поездок на работу на велосипеде и сердечными заболеваниями и частотой курения и сердечными заболеваниями составляет p < 0,001.

Частота сердечных заболеваний снижается на 0,2% (или ± 0,0014) на каждый 1% увеличения количества велосипедистов. Частота сердечных заболеваний увеличивается на 0,178% (или ± 0,0035) на каждый 1% увеличения курения.

Графическое представление результатов

Влияние нескольких независимых переменных на зависимую переменную можно показать на графике. При этом по оси x можно отложить только одну независимую переменную.

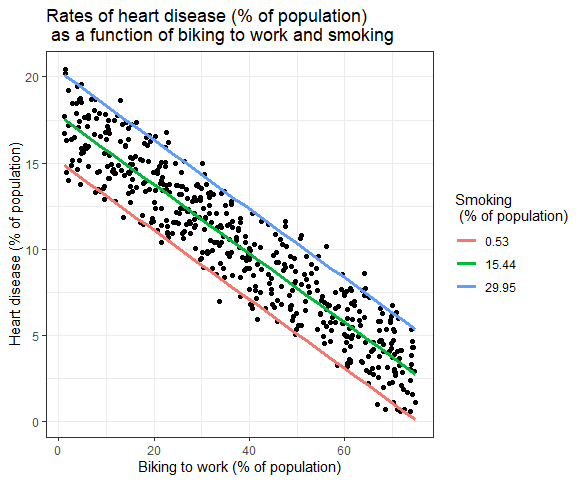
Множественная линейная регрессия: графическое представление

Здесь нанесены предсказанные значения зависимой переменной (заболевания сердца) по наблюдаемым значениям процента людей, которые ездят на работу на велосипеде.

Для влияния курения на независимую переменную рассчитываются прогнозируемые значения, при этом курение остается постоянным при минимальном, среднем и максимальном уровне курения.

Читайте также: Линейная регрессия vs. Логистическая регрессия: разница между линейной регрессией и логистической регрессией

Заключительные слова

На этом пост в блоге заканчивается. Мы приложили все усилия, чтобы объяснить вам концепцию множественной линейной регрессии и то, как множественная регрессия реализована в R для облегчения прогнозного анализа.

Если вы хотите поддержать свое путешествие по науке о данных и изучить больше концепций R и многих других языков, чтобы укрепить свою карьеру, присоединяйтесь к upGrad . Мы предлагаем программу расширенной сертификации в области науки о данных , которая специально разработана для работающих профессионалов и включает более 300 часов обучения с постоянным наставничеством.