数据结构中的表达式解析：符号类型、关联性和优先级

解析是分析一串符号的过程，这些符号以符合形式语法的自然或计算机语言表达。 数据结构中的表达式解析意味着对算术和逻辑表达式的评估。 首先，让我们看看算术表达式是如何写的：

• 9+9
• CB

表达式可以用可以充当运算符或括号的常量、变量和符号来编写。 所有这些表达式都需要遵循一组特定的规则。 根据这个规则，表达式的解析是基于语法来完成的。

算术表达式以 Notation 的形式表示。 现在，有三种方法可以在算术中编写表达式：

• 中缀符号
• 前缀（波兰语）表示法
• 后缀（反向波兰）表示法

但是，在编写表达式时，所需表达式的输出保持不变。 在开始介绍 Notation 的类型之前，让我们看看 Associativity 和 Precedence在数据结构中的表达式解析中是什么。

如果您是初学者并且有兴趣了解有关数据科学的更多信息，请查看我们来自顶尖大学的数据科学课程。

阅读：数据结构中的图

关联性

在开始之前，您需要知道什么是关联性属性； 它为您提供了在表达式中重新排列括号以提供有效证明的规则。 这意味着括号的重新排列需要给出与父方程相同的值。 它提供了替换运算符的有效规则。

在包含两个或多个运算符的表达式中，除非操作数序列不互换，否则执行的操作无关紧要。 如果表达式是使用方括号和中缀编写的，则更改位置不会更改值。

因为在印欧语言中，表达式是从左到右读取的，所以大多数中缀运算符都是左结合的； 运算符的计算优先级相同。 权力上升是考虑中缀运算符时使用的规则。 前缀运算符通常是右关联的，而后缀运算符是左关联的。

在某些语言中，运算符和操作数被赋予相同的值，其中不考虑关联性使该语言序列显式化。 虽然在某些语言中，运算符是非关联的，但这使得使用括号必须使用复杂的表达式，这增加了程序员的复杂性。

数据结构中的优先级

优先顺序是指运算符在表达式语句中需要遵循的顺序。 这通常在使用中缀表示法时使用。

在<operator> <operand> <operator> 操作数介于两个运算符之间的情况下，分配运算符的优先级是相当棘手的。 因此，遵循算子优先规则进行计算。 例如，这里，乘法的优先级较高，然后进行加法运算。

• 最常见但不那么明显的规则是乘法和除法运算必须在加法和减法之前执行。 通常，它们以相同的方式收集，因此为所有操作员提供同等重要性。
• 以逻辑格式考虑此操作，可以在“and”和“or”中看到变化。 许多语言提供同等的重要性，其中“或”操作具有更高的优先级。 一些语言考虑乘法或“&”、“&”加法“或”相等的优先级，其中大多数语言提供具有最高优先级的算术运算。
• 重载是由于没有正确分配优先级引起的。 许多语言提供比向量代数表达式更高的否定（真/假）优先级，而有些语言提供相等的优先级。

另请阅读：数据结构项目理念

符号类型

现在让我们来了解一下操作符的位置如何决定 Notation 的类型。

1. 中缀符号

在中缀表示法中，运算符用于操作数之间。 在阅读表达式时，中缀表示法对人类来说非常容易。 但是当涉及到计算机算法时，处理中缀参数是相当耗费时间和空间的。 例如：p + q

<操作数> <操作数> <操作数>

中缀表示法需要额外的信息来执行评估； 使用运算符Associativity 、 例如：p * ( q + r ) / s

• 关联性规则表明表达式需要从左到右执行，这样 p 的乘法就在 q 的除法之前完成。
• 类似地，优先级规则建议在完成加减运算之前执行乘法和除法运算。

2.前缀表示法

这里先写操作符，然后是操作数。 它也被称为波兰符号。 例如 +pq

<操作符> <操作数> <操作数>

例如： p * ( q + r ) / s

评估需要从左到右进行，括号不会改变或改变方程模式。 这里，加法需要在乘法之前完成，因为位置“+”在“*”的左边。

在这里，每个运算符都对紧邻它们左侧的值执行操作。 例如，上面的“+”使用“q”和“r”。 我们可以总结括号来明确这一点：

((p (qr +) *) s /)

因此，“( )”考虑并使用紧接在“p”之前的两个值，以及 + 的结果。 同样，“/”使用乘法表达式和“s”的结果。

3. 后缀符号

后缀符号，主要是操作数，被写入，然后是一个运算符。 它也被称为逆波兰表示法，例如 pq+

<操作数> <操作数> <操作数>

至于后缀，与表达式的前缀操作一样是从左到右，不需要“( )”。 在这里，运算符对右边最接近的两个值执行。 在下面的示例中，不必要地添加了括号，以表明对评估没有影响。

(/ (* p (+ qr) ) s)

这里“算子评估是从左到右”的操作值在他们的右边，如果值本身涉及计算，那么评估的顺序就会发生变化。 以上面列出的示例为例，“/”是左侧的主要运算符。

它一直等到乘法运算完成。 并且首先需要在除法计算开始之前进行乘法运算（从上面的例子可以看出，在乘法运算之前需要完成加法运算）。

因为 Postfix Notation 运算符使用右边的值； 当我们向左移动时，任何涉及计算的值都将计算已经完成。 因此，我们可以得出结论，表达式计算与前缀运算符操作不同。

为了突出所有三个符号，操作数以相同的顺序出现，并且需要移动运算符以在计算过程中提供正确的含义。 在考虑不对称运算符“-”和“/”时需要特别考虑这一点，以明确 pq 永远是 qr，除非它们具有相同的值； 这些值相当于“pq -”或“- pq”

P+q ≡ +pq ≡ pq+

例如：

中缀- p * q + r / s

前缀 – pq * rs / +

后修复 - + * pq / rs

首先，要执行运算，将 p 和 q 相乘，然后将 r 除以 s，最后将结果相加。

下表简要介绍了三种符号之间的关系，

中缀符号	波兰符号	反向波兰符号
p+q	+pq	q+
(p+q)*r	+*pq	pqr+*
p*(q+r)	*p+qr	pqr*++
p÷q+r÷s	+÷pq÷rs	pq÷rs÷+
(pq)*(rs)	*-pq-rs	pq-rs-*

符号之间的转换

*为了提供清晰的见解，在表达式中添加了括号，

中缀	后缀	字首
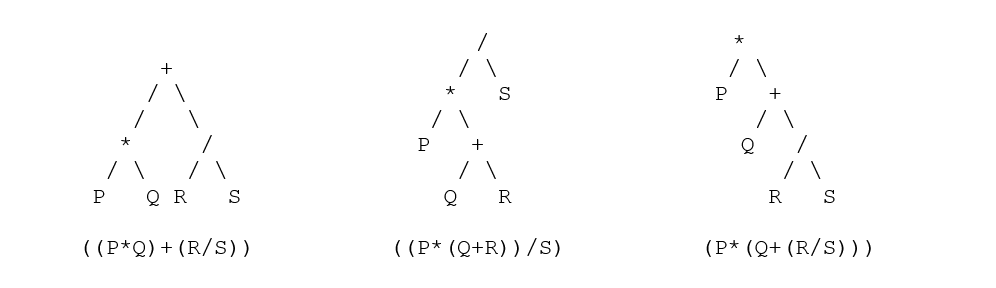
( (p * q) + (r / s) )	( (pq *) (rs /) +)	(+ (* pq) (/ rs) )
((p * (q + r) ) / s)	( (p (qr +) *) s /)	(/ (* p (+ qr) ) s)
(p * (q + (r / s) ) )	(p (q (rs /) +) *)	(* p (+ q (/ rs) ) )

• 您可以通过括号中的运算符直接开始转换括号形式，例如 (m + n) 或 (mn +) 或 (+ mn)。 现在通过删除不需要的括号在所有运算符中重复此操作。
• 现在使用上面显示的这个技巧来转换和解析树 - 每个节点的等效解析树是：

结帐： Python中的数据结构和算法

结论

数据结构中的表达式解析，算术表达式中的中缀、后缀和前缀表示法是完全不同的，但具有相同的表达式编写方式。 这些知识对于编写程序至关重要。

在计算机编程语言中，表达式是从字符串中考虑和解析的。 关联性和优先级规则在不同语言中发生了很大变化。

为什么选择 upGrad 的数据科学课程？

数据科学是计算机科学中蓬勃发展的领域之一。 公司需要具有良好基础知识的程序员，这是编程的基础，而与编码语言无关。

upGrad 专注于提供富有洞察力和信息丰富的课程，涵盖成为数据科学家的所有基本需求。 upGrad 为期 12 个月的数据科学执行 PG 计划。 由 IIIT Bangalore 提供，是印度第一个 NASSCOM 认证课程，由数据科学行业专家提供 1:1 个性化指导，涵盖所有基本的编程语言、工具和库。 它为您开始高薪数据科学工作提供了最佳基础。

什么是数据结构？

数据结构用于组织内存中的数据。 有几种方法可以在内存中排列数据，包括数组、列表、堆栈、队列等。 数据结构不是像 C、C++ 或 Java 那样的编程语言。 相反，它是一组用于以任何编程语言在内存中排列数据的技术。 数据结构是一种有效组织、处理和存储数据的方法。 在数据结构的帮助下，可以简单地遍历数据项。 这对于提高程序的速度至关重要，因为程序的主要工作是尽可能快地保存和检索用户的数据。

数据解析的实际用途是什么？

将数据从一种格式转换为另一种格式的过程称为数据解析。 它们广泛用于编译器中，用于解析计算机代码和生成机器代码。 将数据从一种格式转换为另一种格式的过程称为数据解析。 因为我们收到的原始 HTML 很难理解，所以解析器经常用于在线抓取。 我们要求将数据转换为人类可读的格式。 这可能意味着使用 HTML 字符串或表格构建报告以提供最相关的信息。

关联性和优先级如何帮助数据结构化？

表达式的求值顺序由运算符的两个属性决定：优先级和关联性。 优先级有助于确定表达式中的术语应如何分组以及如何评估表达式。 因为大多数表达式使用 BODMAS 框架，某些运算符优先于其他运算符。 当两个运算符在表达式中具有相同的优先级时，将应用关联规则。 根据编译器的偏好，关联性可能是从左到右或从右到左。