决策树的基尼指数：机制，完美和不完美的拆分示例

介绍

决策树是监督学习中最常用的实用方法之一。 它可用于解决回归和分类任务，后者更多地投入实际应用。 在这些树中，类标签由叶子表示，分支表示导致这些类标签的特征的结合。 它广泛用于机器学习算法。 通常，机器学习方法包括控制许多超参数和优化。

当预测结果为实数时使用回归树，分类树用于预测数据所属的类别。 这两个术语统称为分类和回归树 (CART)。

这些是提供回归或分类树的非参数决策树学习技术，分别取决于因变量是分类变量还是数值变量。 该算法采用基尼指数的方法来发起二元分裂。 基尼指数和基尼杂质可以互换使用。

决策树影响了机器学习中的回归模型。 在设计树时，开发人员使用边设置节点的特征和该特征的可能属性。

计算

基尼指数或基尼杂质是通过从 1 中减去每个类别的概率平方和来计算的。 它主要支持较大的分区，并且实现起来非常简单。 简单来说，它计算某个随机选择的特征被错误分类的概率。

基尼指数在 0 和 1 之间变化，其中 0 表示分类的纯度，1 表示元素在各个类别中的随机分布。 基尼指数为 0.5 表明在某些类别中元素的分布是相等的。

在数学上，基尼指数表示为

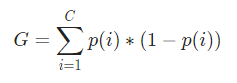
基尼指数适用于分类变量，并根据“成功”或“失败”给出结果，因此只执行二元拆分。 它不像其对应的信息增益那样计算密集。 根据基尼指数，计算另一个名为 Gini Gain 的参数的值，其值在决策树的每次迭代中最大化，以获得完美的 CART

让我们通过一个简单的例子来理解基尼指数的计算。 在这里，我们总共有 10 个数据点，其中有两个变量，红色和蓝色。 X 轴和 Y 轴以每项之间的 100 间隔编号。 从给定的例子中，我们将计算基尼指数和基尼增益。

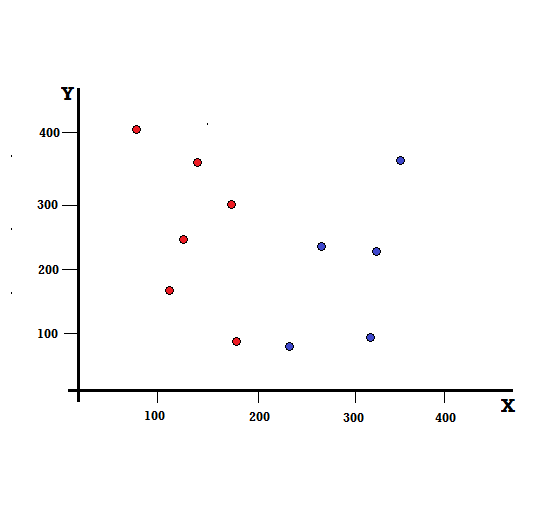
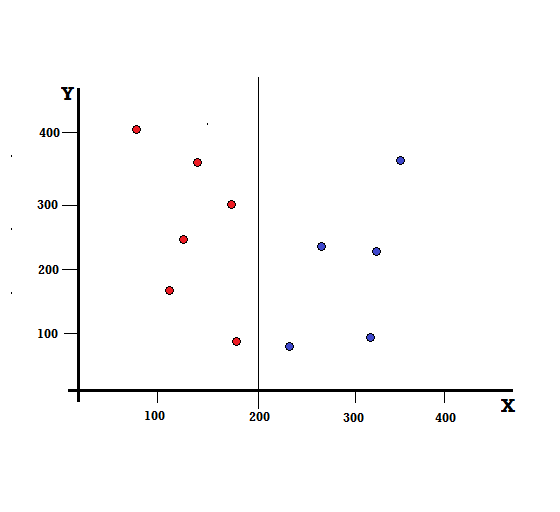
对于决策树，我们需要将数据集分成两个分支。 考虑以下在 XY 平面上标记了 5 个红色和 5 个蓝色的数据点。 假设我们在 X=200 处进行二元拆分，那么我们将得到如下所示的完美拆分。

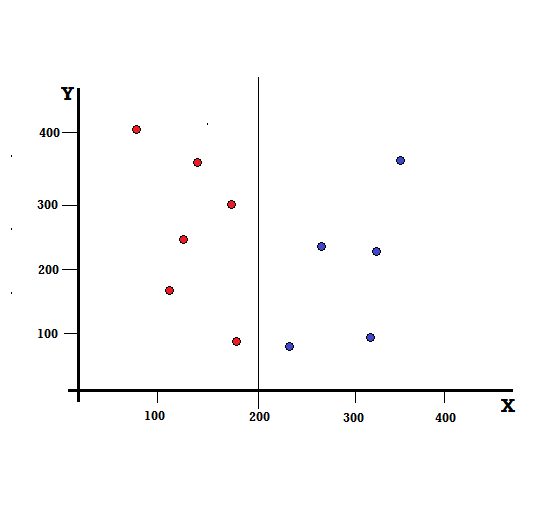
可以看出，拆分是正确执行的，我们剩下两个分支，每个分支有 5 个红色（左分支）和 5 个蓝色（右分支）。

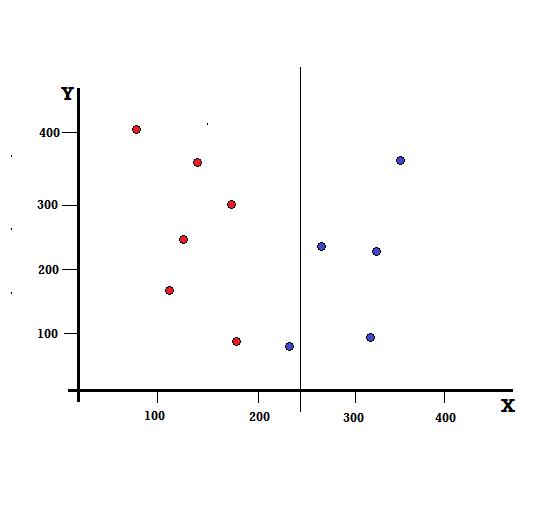
但是，如果我们在 X=250 处进行拆分，结果会是什么？

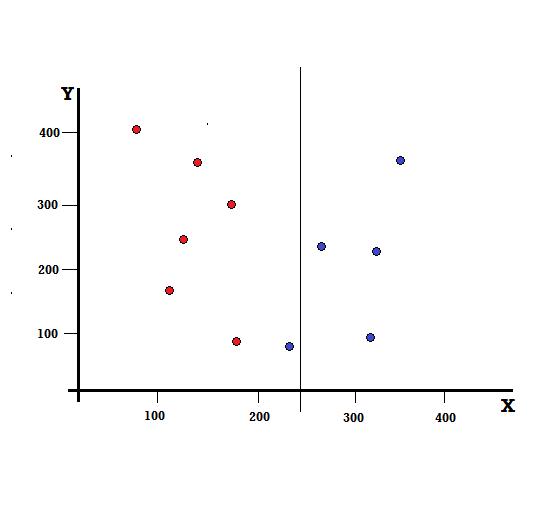
我们剩下两个分支，左分支由 5 个红色和 1 个蓝色组成，而右分支由 4 个蓝色组成。 以下称为不完美分裂。 在训练决策树模型时，为了量化分裂的不完美程度，我们可以使用基尼指数。

结帐：二叉树的类型

基本机制

计算基尼杂质，让我们首先了解它的基本机制。

• 首先，我们将从数据集中随机选取任何数据点
• 然后，我们将根据给定数据集中的类分布对其进行随机分类。 在我们的数据集中，我们将给出一个数据点，选择红色的概率为 5/10，蓝色的概率为 5/10，因为每种颜色有五个数据点，因此概率。

现在，为了计算基尼指数，公式如下

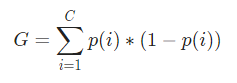
其中，C 是类的总数，p( i )​​ 是选择具有类i 的数据点的概率。

在上面的例子中，我们有 C=2 和 p(1) = p(2) = 0.5，因此基尼指数可以计算为，

G =p(1) ∗ (1−p(1)) + p(2) ∗ (1−p(2))

=0.5 * (1−0.5) + 0.5 * (1−0.5)

=0.5

其中 0.5 是对数据点进行不完美分类的总概率，因此正好是 50%。

现在，让我们计算我们之前执行的完美和不完美分割的基尼杂质，

完美分裂

左分支只有红色，因此它的基尼杂质是，

G(左) =1 * (1−1) + 0 * (1−0) = 0

右支也只有布鲁斯，因此它的基尼杂质也由下式给出，

G(右) =1 * (1−1) + 0 * (1−0) = 0

通过快速计算，我们看到完美分割的左右分支的概率均为 0，因此确实是完美的。 对于任何数据集，基尼杂质 0 是最低和最好的杂质。

不完美分裂

在这种情况下，左分支有 5 个红色和 1 个蓝色。 它的基尼杂质可以通过以下方式给出，

G(左) =1/6 * (1−1/6) + 5/6 * (1−5/6) = 0.278

右分支全部为蓝色，因此如上计算，其基尼杂质由下式给出，

G(右) =1 * (1−1) + 0 * (1−0) = 0

既然我们有了不完美分裂的基尼杂质，为了评估分裂的质量或程度，我们将用它所具有的元素数量对每个分支的杂质赋予特定的权重。

(0.6 * 0.278) + (0.4 * 0) = 0.167

现在我们已经计算了基尼指数，我们将计算另一个参数的值，基尼增益并分析其在决策树中的应用。 通过使用整个数据集的基尼指数（0.5）减去上述值来计算通过此拆分去除的杂质量

0.5 – 0.167 = 0.333

计算出的这个值称为“基尼增益”。 简单来说，更高的基尼增益 = 更好的分割。

因此，在决策树算法中，通过最大化 Gini Gain 来获得最佳分割，该 Gini Gain 是在每次迭代时以上述方式计算的。

在计算数据集中每个属性的 Gini Gain 后，类 sklearn.tree.DecisionTreeClassifier 将选择最大的 Gini Gain 作为 Root Node。 当遇到 Gini 为 0 的分支时，它将成为叶节点，而 Gini 大于 0 的其他分支需要进一步分裂。 这些节点递归地增长，直到它们都被分类。

在机器学习中使用

在机器学习的世界中，有多种算法针对不同的目的而设计。 问题在于确定哪种算法最适合给定数据集。 决策树算法似乎也显示出令人信服的结果。 要认识到这一点，人们必须认为决策树在某种程度上模仿了人类的主观能力。

因此，具有更多人类认知问题的问题可能更适合决策树。 决策树的基本概念因其树状结构而易于理解。

另请阅读：人工智能中的决策树：简介、类型和创建

结论

基尼指数的替代方案是信息熵，它用于确定哪个属性为我们提供了关于一个类的最大信息。 它基于熵的概念，熵是杂质或不确定性的程度。 它旨在降低从根节点到决策树叶节点的熵水平。

通过这种方式，CART 算法使用基尼指数来优化决策树并为分类树创建决策点。

如果您有兴趣了解有关机器学习的更多信息，请查看 IIIT-B 和 upGrad 的机器学习和人工智能 PG 文凭，该文凭专为工作专业人士设计，提供 450 多个小时的严格培训、30 多个案例研究和作业、IIIT- B 校友身份、5 个以上实用的实践顶点项目和顶级公司的工作协助。