Indeks Gini untuk Pohon Keputusan: Mekanisme, Pemisahan Sempurna & Tidak Sempurna Dengan Contoh

pengantar

Pohon Keputusan adalah salah satu pendekatan praktis yang paling umum digunakan untuk pembelajaran terawasi. Ini dapat digunakan untuk menyelesaikan tugas Regresi dan Klasifikasi dengan yang terakhir lebih banyak diterapkan dalam aplikasi praktis. Dalam pohon ini, label kelas diwakili oleh daun dan cabang menunjukkan konjungsi fitur yang mengarah ke label kelas tersebut. Ini banyak digunakan dalam algoritma pembelajaran mesin. Biasanya, pendekatan pembelajaran mesin mencakup pengendalian banyak hiperparameter dan pengoptimalan.

Pohon regresi digunakan ketika hasil yang diprediksi adalah bilangan real dan pohon klasifikasi digunakan untuk memprediksi kelas tempat data tersebut berada. Kedua istilah ini secara kolektif disebut sebagai Pohon Klasifikasi dan Regresi (CART).

Ini adalah teknik pembelajaran pohon keputusan non-parametrik yang menyediakan pohon regresi atau klasifikasi, bergantung pada apakah variabel terikatnya masing-masing kategoris atau numerik. Algoritma ini menyebarkan metode Indeks Gini untuk memulai pemisahan biner. Baik Gini Index dan Gini Impurity digunakan secara bergantian.

Pohon keputusan telah memengaruhi model regresi dalam pembelajaran mesin. Saat mendesain pohon, pengembang mengatur fitur node dan atribut yang mungkin dari fitur tersebut dengan tepi.

Perhitungan

Gini Index atau Gini Impurity dihitung dengan mengurangkan jumlah kuadrat dari probabilitas setiap kelas dari satu. Ini mendukung sebagian besar partisi yang lebih besar dan sangat sederhana untuk diterapkan. Secara sederhana, ini menghitung probabilitas fitur tertentu yang dipilih secara acak yang diklasifikasikan secara tidak benar.

Indeks Gini bervariasi antara 0 dan 1, di mana 0 mewakili kemurnian klasifikasi dan 1 menunjukkan distribusi elemen secara acak di antara berbagai kelas. Indeks Gini sebesar 0,5 menunjukkan bahwa ada distribusi elemen yang sama di beberapa kelas.

Secara matematis, Indeks Gini diwakili oleh

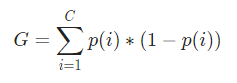
Indeks Gini bekerja pada variabel kategori dan memberikan hasil dalam istilah "berhasil" atau "gagal" dan karenanya hanya melakukan pemisahan biner. Ini tidak intensif secara komputasi seperti padanannya – Perolehan Informasi. Dari Gini Index dihitung nilai parameter lain yang bernama Gini Gain yang nilainya dimaksimalkan dengan setiap iterasi oleh Decision Tree untuk mendapatkan CART yang sempurna.

Mari kita pahami perhitungan Gini Index dengan contoh sederhana. Dalam hal ini, kami memiliki total 10 titik data dengan dua variabel, merah dan biru. Sumbu X dan Y diberi nomor dengan spasi 100 di antara setiap suku. Dari contoh yang diberikan, kita akan menghitung Gini Index dan Gini Gain.

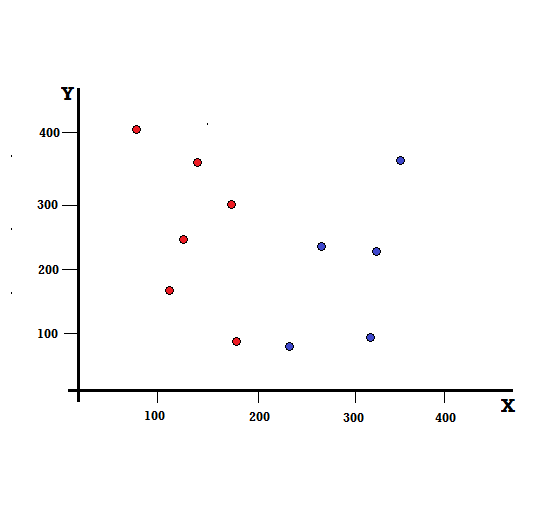
Untuk pohon keputusan, kita perlu membagi dataset menjadi dua cabang. Perhatikan titik data berikut dengan 5 Merah dan 5 Biru yang ditandai pada bidang XY. Misalkan kita membuat split biner pada X=200, maka kita akan memiliki split sempurna seperti yang ditunjukkan di bawah ini.

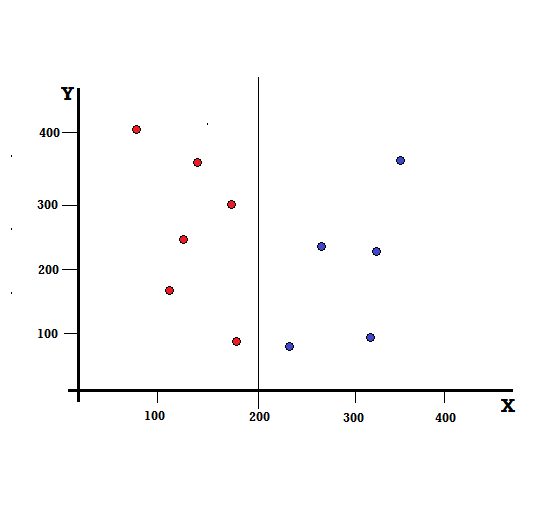
Terlihat bahwa split dilakukan dengan benar dan kita dibiarkan dengan dua cabang masing-masing dengan 5 merah (cabang kiri) dan 5 biru (cabang kanan).

Tapi apa yang akan terjadi jika kita melakukan split pada X=250?

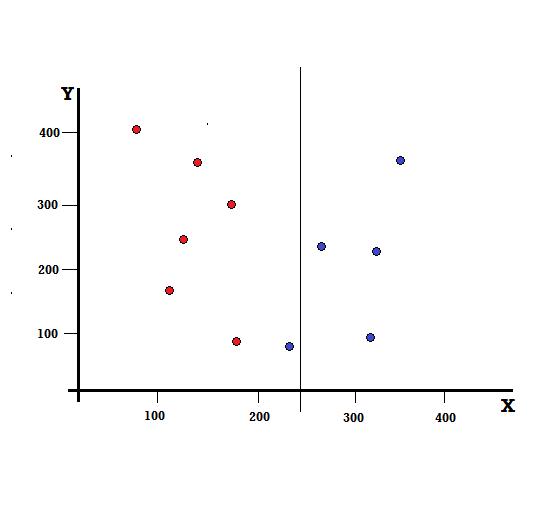
Kita dibiarkan dengan dua cabang, cabang kiri terdiri dari 5 merah dan 1 biru, sedangkan cabang kanan terdiri dari 4 biru. Berikut ini disebut sebagai perpecahan tidak sempurna. Dalam melatih model Pohon Keputusan, untuk mengukur jumlah ketidaksempurnaan pemisahan, kita dapat menggunakan Indeks Gini.

Checkout: Jenis Pohon Biner

Mekanisme Dasar

Untuk menghitung Gini Impurity , mari kita pahami dulu mekanisme dasarnya.

• Pertama, kami akan secara acak mengambil titik data apa pun dari kumpulan data
• Kemudian, kita akan mengklasifikasikannya secara acak sesuai dengan distribusi kelas pada dataset yang diberikan. Dalam dataset kami, kami akan memberikan titik data yang dipilih dengan probabilitas 5/10 untuk merah dan 5/10 untuk biru karena ada lima titik data dari setiap warna dan karenanya probabilitas.

Sekarang, untuk menghitung Indeks Gini, rumusnya diberikan oleh

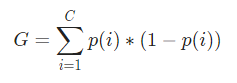
Dimana, C adalah jumlah kelas dan p( i ) adalah peluang terambilnya titik data dengan kelas i.

Dalam contoh di atas, kita memiliki C=2 dan p(1) = p(2) = 0,5, Oleh karena itu Indeks Gini dapat dihitung sebagai,

G =p(1) ( 1−p(1)) + p(2) ( 1 −p(2))

=0,5 ( 1−0,5 ) + 0,5 ( 1−0,5 )

= 0,5

Dimana 0,5 adalah probabilitas total untuk mengklasifikasikan titik data secara tidak sempurna dan karenanya tepat 50%.

Sekarang, mari kita hitung Gini Impurity untuk split sempurna dan tidak sempurna yang kita lakukan sebelumnya,

Perpecahan Sempurna

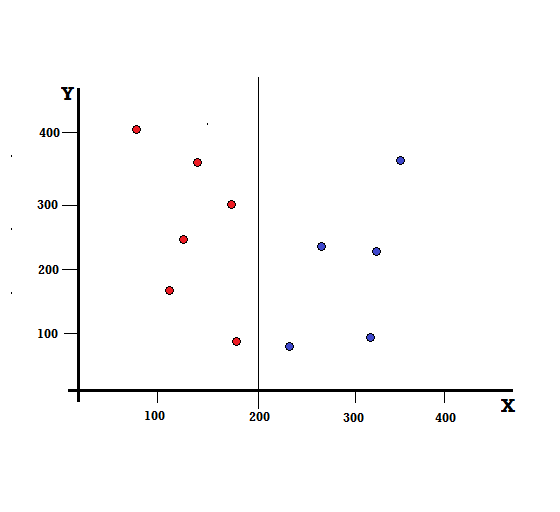
Cabang kiri hanya memiliki warna merah dan karenanya Gini Impurity-nya adalah,

G(kiri) =1 ( 1−1) + 0 ( 1−0 ) = 0

Cabang kanan juga hanya memiliki blues dan karenanya Gini Impurity-nya juga diberikan oleh,

G(kanan) =1 ( 1−1) + 0 ( 1−0 ) = 0

Dari perhitungan cepat, kita melihat bahwa kedua cabang kiri dan kanan dari pemisahan sempurna kita memiliki probabilitas 0 dan karenanya memang sempurna. Pengotor Gini 0 adalah pengotor terendah dan terbaik untuk kumpulan data apa pun.

Perpecahan Tidak Sempurna

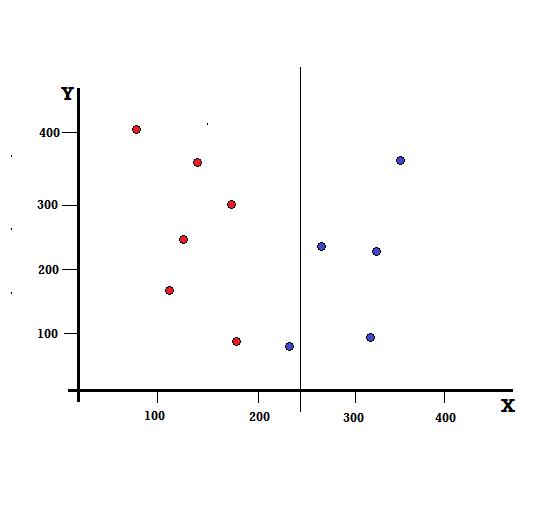
Dalam hal ini, cabang kiri memiliki 5 merah dan 1 biru. Gini Impurity-nya dapat diberikan oleh,

G(kiri) =1/6 ( 1−1/6) + 5/6 ( 1−5 /6) = 0,278

Cabang kanan memiliki semua blues dan karenanya seperti yang dihitung di atas Gini Impurity-nya diberikan oleh,

G(kanan) =1 ( 1−1) + 0 ( 1−0 ) = 0

Sekarang kita memiliki Kotoran Gini dari pemisahan yang tidak sempurna, untuk mengevaluasi kualitas atau tingkat pemisahan, kita akan memberikan bobot khusus untuk pengotor setiap cabang dengan jumlah elemen yang dimilikinya.

(0,6 0,278 ) + (0,4 0) = 0,167

Sekarang kita telah menghitung Indeks Gini, kita akan menghitung nilai parameter lain, Gain Gini dan menganalisis penerapannya di Pohon Keputusan. Jumlah pengotor yang dihilangkan dengan pemisahan ini dihitung dengan mengurangi nilai di atas dengan Indeks Gini untuk seluruh kumpulan data (0,5)

0,5 – 0,167 = 0,333

Nilai yang dihitung ini disebut sebagai “ Gini Gain ”. Dalam istilah sederhana, Keuntungan Gini Lebih Tinggi = Split Lebih Baik .

Oleh karena itu, dalam algoritma Decision Tree, split terbaik diperoleh dengan memaksimalkan Gini Gain, yang dihitung dengan cara di atas pada setiap iterasi.

Setelah menghitung Gini Gain untuk setiap atribut dalam kumpulan data, kelas, sklearn.tree.DecisionTreeClassifier akan memilih Gini Gain terbesar sebagai Root Node. Ketika sebuah cabang dengan Gini 0 ditemui, itu menjadi simpul daun dan cabang-cabang lain dengan Gini lebih dari 0 membutuhkan pemisahan lebih lanjut. Node-node ini ditumbuhkan secara rekursif sampai semuanya diklasifikasikan.

Gunakan dalam Pembelajaran Mesin

Ada berbagai algoritma yang dirancang untuk tujuan yang berbeda di dunia pembelajaran mesin. Masalahnya terletak pada mengidentifikasi algoritma mana yang paling sesuai dengan dataset yang diberikan. Algoritme pohon keputusan tampaknya juga menunjukkan hasil yang meyakinkan. Untuk mengenalinya, orang harus berpikir bahwa pohon keputusan agak meniru kekuatan subjektif manusia.

Jadi, masalah dengan lebih banyak pertanyaan kognitif manusia cenderung lebih cocok untuk pohon keputusan. Konsep yang mendasari pohon keputusan dapat dengan mudah dimengerti karena strukturnya yang seperti pohon.

Baca Juga: Pohon Keputusan di AI: Pengenalan, Jenis & Kreasi

Kesimpulan

Alternatif untuk Gini Index adalah Entropi Informasi yang digunakan untuk menentukan atribut mana yang memberi kita informasi maksimum tentang suatu kelas. Ini didasarkan pada konsep entropi, yang merupakan tingkat ketidakmurnian atau ketidakpastian. Hal ini bertujuan untuk menurunkan tingkat entropi dari simpul akar ke simpul daun dari pohon keputusan.

Dengan cara ini, Indeks Gini digunakan oleh algoritma CART untuk mengoptimalkan pohon keputusan dan membuat titik keputusan untuk pohon klasifikasi.

Jika Anda tertarik untuk mempelajari lebih lanjut tentang pembelajaran mesin, lihat PG Diploma IIIT-B & upGrad dalam Pembelajaran Mesin & AI yang dirancang untuk para profesional yang bekerja dan menawarkan 450+ jam pelatihan ketat, 30+ studi kasus & tugas, IIIT- B Status alumni, 5+ proyek batu penjuru praktis & bantuan pekerjaan dengan perusahaan-perusahaan top.