Gini-Index für Entscheidungsbäume: Mechanismus, perfekte & unvollkommene Aufteilung mit Beispielen

Einführung

Entscheidungsbaum ist einer der am häufigsten verwendeten, praktischen Ansätze für überwachtes Lernen. Es kann verwendet werden, um sowohl Regressions- als auch Klassifizierungsaufgaben zu lösen, wobei letztere mehr in die praktische Anwendung gebracht werden. In diesen Bäumen werden die Klassenbezeichnungen durch die Blätter dargestellt, und die Zweige bezeichnen die Verbindungen von Merkmalen, die zu diesen Klassenbezeichnungen führen. Es wird häufig in maschinellen Lernalgorithmen verwendet. Typischerweise umfasst ein maschineller Lernansatz die Steuerung vieler Hyperparameter und Optimierungen.

Der Regressionsbaum wird verwendet, wenn das vorhergesagte Ergebnis eine reelle Zahl ist, und der Klassifizierungsbaum wird verwendet, um die Klasse vorherzusagen, zu der die Daten gehören. Diese beiden Begriffe werden gemeinsam als Klassifikations- und Regressionsbäume (CART) bezeichnet.

Dies sind nichtparametrische Lerntechniken für Entscheidungsbäume, die Regressions- oder Klassifikationsbäume bereitstellen, je nachdem, ob die abhängige Variable kategorial oder numerisch ist. Dieser Algorithmus setzt die Methode von Gini Index ein, um binäre Splits zu erstellen. Sowohl Gini Index als auch Gini Impurity werden synonym verwendet.

Entscheidungsbäume haben Regressionsmodelle im maschinellen Lernen beeinflusst. Beim Entwerfen des Baums legen Entwickler die Merkmale der Knoten und die möglichen Attribute dieses Merkmals mit Kanten fest.

Berechnung

Der Gini-Index oder die Gini-Verunreinigung wird berechnet, indem die Summe der quadrierten Wahrscheinlichkeiten jeder Klasse von eins subtrahiert wird. Es bevorzugt hauptsächlich die größeren Partitionen und ist sehr einfach zu implementieren. Vereinfacht ausgedrückt berechnet es die Wahrscheinlichkeit, dass ein bestimmtes zufällig ausgewähltes Merkmal falsch klassifiziert wurde.

Der Gini-Index variiert zwischen 0 und 1, wobei 0 die Reinheit der Klassifikation darstellt und 1 die zufällige Verteilung von Elementen auf verschiedene Klassen bezeichnet. Ein Gini-Index von 0,5 zeigt, dass die Elemente in einigen Klassen gleichmäßig verteilt sind.

Mathematisch wird der Gini-Index dargestellt durch

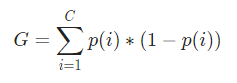
Der Gini-Index arbeitet mit kategorialen Variablen und gibt die Ergebnisse in Form von „Erfolg“ oder „Misserfolg“ an und führt daher nur eine binäre Aufteilung durch. Es ist nicht rechenintensiv wie sein Gegenstück – Informationsgewinn. Aus dem Gini-Index wird der Wert eines anderen Parameters namens Gini Gain berechnet, dessen Wert bei jeder Iteration durch den Entscheidungsbaum maximiert wird, um den perfekten CART zu erhalten

Lassen Sie uns die Berechnung des Gini-Index an einem einfachen Beispiel nachvollziehen. Darin haben wir insgesamt 10 Datenpunkte mit zwei Variablen, den Roten und den Blauen. Die X- und Y-Achsen sind mit Leerzeichen von 100 zwischen jedem Begriff nummeriert. Aus dem gegebenen Beispiel berechnen wir den Gini-Index und den Gini-Gewinn.

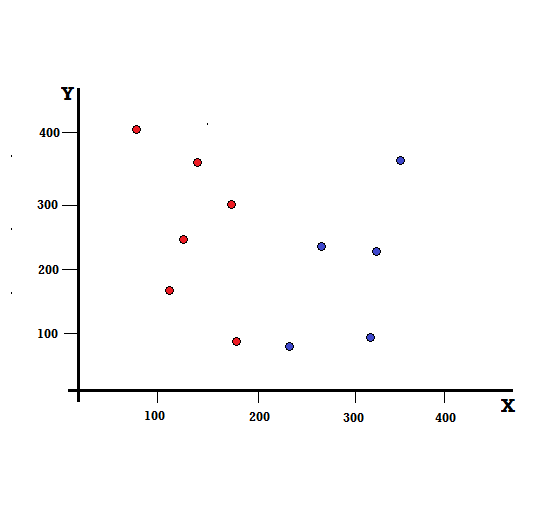
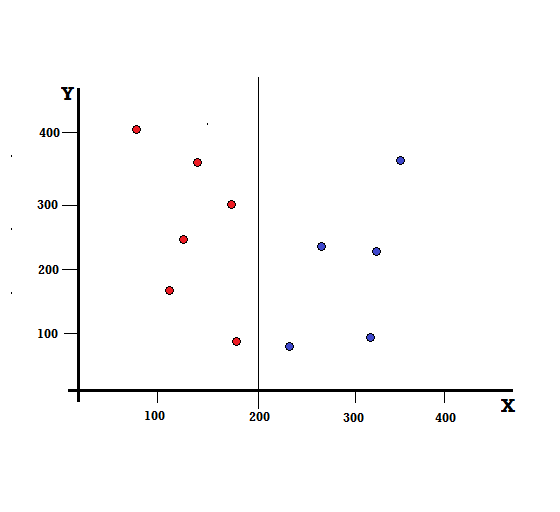
Für einen Entscheidungsbaum müssen wir den Datensatz in zwei Zweige aufteilen. Betrachten Sie die folgenden Datenpunkte mit 5 roten und 5 blauen Markierungen auf der XY-Ebene. Angenommen, wir machen eine binäre Teilung bei X = 200, dann haben wir eine perfekte Teilung, wie unten gezeigt.

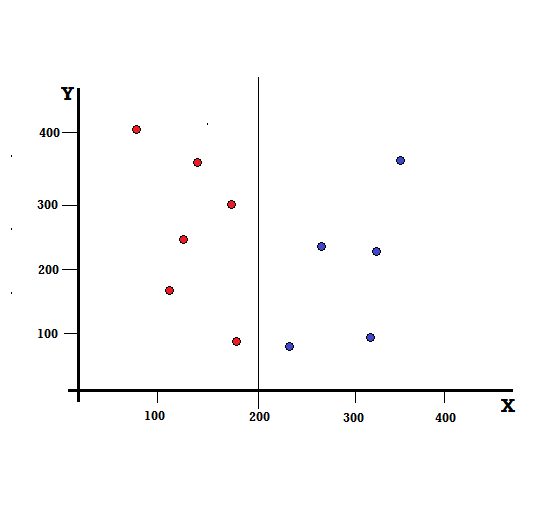
Es ist ersichtlich, dass die Teilung korrekt durchgeführt wird und wir zwei Zweige mit jeweils 5 Roten (linker Zweig) und 5 Blauen (rechter Zweig) übrig haben.

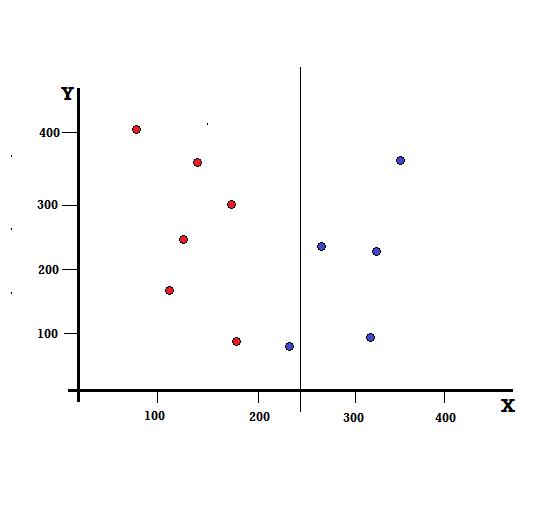
Aber was wird das Ergebnis sein, wenn wir die Aufteilung bei X=250 vornehmen?

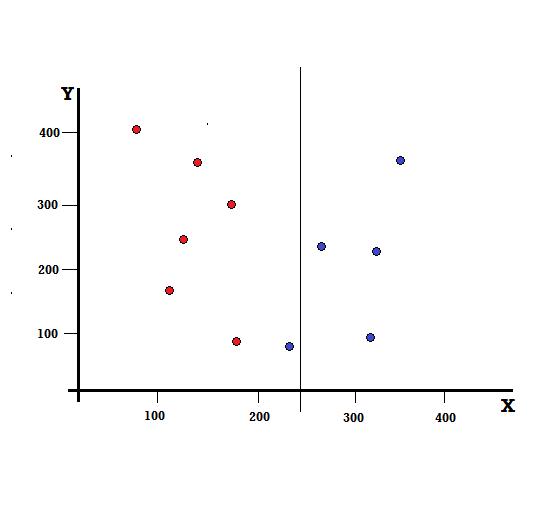
Wir haben zwei Zweige übrig, der linke Zweig besteht aus 5 roten und 1 blauen, während der rechte Zweig aus 4 blauen besteht. Das Folgende wird als unvollkommene Teilung bezeichnet. Beim Trainieren des Entscheidungsbaummodells können wir den Gini-Index verwenden, um das Ausmaß der Unvollkommenheit der Aufteilung zu quantifizieren.

Checkout: Arten von Binärbäumen

Grundlegender Mechanismus

Um die Gini - Verunreinigung zu berechnen , wollen wir zunächst ihren grundlegenden Mechanismus verstehen.

• Zunächst werden wir zufällig einen beliebigen Datenpunkt aus dem Datensatz auswählen
• Dann werden wir es zufällig gemäß der Klassenverteilung im gegebenen Datensatz klassifizieren. In unserem Datensatz geben wir einen Datenpunkt an, der mit einer Wahrscheinlichkeit von 5/10 für Rot und 5/10 für Blau ausgewählt wurde, da es fünf Datenpunkte für jede Farbe und daher die Wahrscheinlichkeit gibt.

Um nun den Gini-Index zu berechnen, ist die Formel gegeben durch

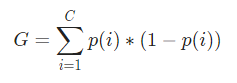
Wobei C die Gesamtzahl der Klassen und p( i ) die Wahrscheinlichkeit ist, den Datenpunkt mit der Klasse i auszuwählen.

Im obigen Beispiel haben wir C = 2 und p (1) = p (2) = 0,5. Daher kann der Gini-Index wie folgt berechnet werden:

G =p(1) ∗ (1−p(1)) + p(2) ∗ (1−p(2))

=0,5 ∗ (1−0,5) + 0,5 ∗ (1−0,5)

=0,5

Wobei 0,5 die Gesamtwahrscheinlichkeit ist, einen Datenpunkt unvollkommen zu klassifizieren und somit genau 50 % beträgt.

Lassen Sie uns nun die Gini-Unreinheit sowohl für die perfekte als auch für die unvollkommene Aufteilung berechnen, die wir zuvor durchgeführt haben.

Perfekte Trennung

Der linke Zweig hat nur Rottöne und daher ist seine Gini-Verunreinigung,

G(links) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Der rechte Zweig hat auch nur Blues und daher ist seine Gini-Unreinheit auch gegeben durch,

G(rechts) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Aus der schnellen Berechnung sehen wir, dass sowohl der linke als auch der rechte Zweig unserer perfekten Aufteilung Wahrscheinlichkeiten von 0 haben und daher tatsächlich perfekt ist. Eine Gini-Verunreinigung von 0 ist die niedrigste und bestmögliche Verunreinigung für jeden Datensatz.

Unvollkommene Trennung

In diesem Fall hat der linke Zweig 5 rote und 1 blaue. Seine Gini-Unreinheit kann gegeben werden durch,

G(links) =1/6 ∗ (1−1/6) + 5/6 ∗ (1−5/6) = 0,278

Der rechte Zweig hat alle Blues und daher ist seine Gini-Verunreinigung wie oben berechnet gegeben durch:

G(rechts) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Nachdem wir nun die Gini-Verunreinigungen der unvollkommenen Teilung haben, werden wir, um die Qualität oder das Ausmaß der Teilung zu bewerten, der Unreinheit jedes Zweigs mit der Anzahl der Elemente, die er hat, ein spezifisches Gewicht geben.

(0,6 ∗ 0,278) + (0,4 ∗ 0) = 0,167

Nachdem wir den Gini-Index berechnet haben, berechnen wir den Wert eines anderen Parameters, Gini Gain, und analysieren seine Anwendung in Entscheidungsbäumen. Die Menge der mit dieser Aufteilung entfernten Verunreinigungen wird berechnet, indem der obige Wert mit dem Gini-Index für den gesamten Datensatz (0,5) abgezogen wird.

0,5 – 0,167 = 0,333

Dieser berechnete Wert wird als „ Gini-Gewinn “ bezeichnet. Einfach ausgedrückt: Höherer Gini-Gewinn = Besserer Split .

Daher wird in einem Entscheidungsbaumalgorithmus die beste Teilung durch Maximieren der Gini-Verstärkung erhalten, die bei jeder Iteration auf die obige Weise berechnet wird.

Nach der Berechnung des Gini-Gewinns für jedes Attribut im Datensatz wählt die Klasse sklearn.tree.DecisionTreeClassifier den größten Gini-Gewinn als Wurzelknoten. Wenn ein Zweig mit einem Gini von 0 angetroffen wird, wird er zum Blattknoten, und die anderen Zweige mit einem Gini von mehr als 0 müssen weiter aufgeteilt werden. Diese Knoten werden rekursiv gewachsen, bis sie alle klassifiziert sind.

Verwendung im maschinellen Lernen

In der Welt des maschinellen Lernens gibt es verschiedene Algorithmen, die für unterschiedliche Zwecke entwickelt wurden. Das Problem liegt darin, zu identifizieren, welcher Algorithmus für einen bestimmten Datensatz am besten geeignet ist. Auch der Entscheidungsbaum-Algorithmus scheint überzeugende Ergebnisse zu zeigen. Um dies zu erkennen, muss man denken, dass Entscheidungsbäume in gewisser Weise menschliche subjektive Macht nachahmen.

Daher ist ein Problem mit eher menschlichen kognitiven Fragen wahrscheinlich besser für Entscheidungsbäume geeignet. Das zugrunde liegende Konzept von Entscheidungsbäumen ist aufgrund seiner baumartigen Struktur leicht verständlich.

Lesen Sie auch: Entscheidungsbaum in der KI: Einführung, Typen und Erstellung

Fazit

Eine Alternative zum Gini-Index ist die Informationsentropie, mit der bestimmt wurde, welches Attribut uns die maximale Information über eine Klasse gibt. Es basiert auf dem Konzept der Entropie, das ist der Grad der Verunreinigung oder Ungewissheit. Es zielt darauf ab, das Entropieniveau von den Wurzelknoten zu den Blattknoten des Entscheidungsbaums zu verringern.

Auf diese Weise wird der Gini-Index von den CART-Algorithmen verwendet, um die Entscheidungsbäume zu optimieren und Entscheidungspunkte für Klassifizierungsbäume zu erstellen.

Wenn Sie mehr über maschinelles Lernen erfahren möchten, sehen Sie sich das PG-Diplom in maschinellem Lernen und KI von IIIT-B & upGrad an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenge Schulungen, mehr als 30 Fallstudien und Aufgaben bietet, IIIT- B-Alumni-Status, mehr als 5 praktische, praktische Abschlussprojekte und Jobunterstützung bei Top-Unternehmen.