مؤشر جيني لأشجار القرار: آلية ، انقسام كامل وغير كامل مع أمثلة

مقدمة

شجرة القرار هي واحدة من أكثر الأساليب العملية شيوعًا للتعلم تحت الإشراف. يمكن استخدامه لحل كل من مهام الانحدار والتصنيف مع وضع الأخير في التطبيق العملي. في هذه الأشجار ، يتم تمثيل تسميات الفصل بالأوراق وتشير الفروع إلى اقتران السمات التي تؤدي إلى تسميات الفئات تلك. يستخدم على نطاق واسع في خوارزميات التعلم الآلي. عادةً ما يتضمن نهج التعلم الآلي التحكم في العديد من المعلمات الفائقة والتحسينات.

تُستخدم شجرة الانحدار عندما تكون النتيجة المتوقعة رقمًا حقيقيًا وتستخدم شجرة التصنيف للتنبؤ بالفئة التي تنتمي إليها البيانات. يُطلق على هذين المصطلحين معًا اسم أشجار التصنيف والانحدار (CART).

هذه تقنيات تعلم شجرة قرارات غير معلمية توفر أشجار الانحدار أو التصنيف ، بالاعتماد على ما إذا كان المتغير التابع فئويًا أم عدديًا على التوالي. تنشر هذه الخوارزمية طريقة مؤشر جيني لإنشاء الانقسامات الثنائية. يتم استخدام كل من مؤشر جيني ونجاسة جيني بالتبادل.

أثرت أشجار القرار على نماذج الانحدار في التعلم الآلي. أثناء تصميم الشجرة ، يقوم المطورون بتعيين ميزات العقد والسمات المحتملة لتلك الميزة مع الحواف.

عملية حسابية

يتم حساب مؤشر جيني أو شائبة جيني بطرح مجموع الاحتمالات التربيعية لكل فئة من واحد. يفضل في الغالب الأقسام الكبيرة ويسهل تنفيذه. بعبارات بسيطة ، تقوم بحساب احتمال ميزة معينة تم اختيارها عشوائيًا تم تصنيفها بشكل غير صحيح.

يختلف مؤشر جيني بين 0 و 1 ، حيث يمثل 0 نقاء التصنيف و 1 يشير إلى التوزيع العشوائي للعناصر بين الفئات المختلفة. يوضح مؤشر جيني 0.5 أن هناك توزيعًا متساويًا للعناصر عبر بعض الفئات.

رياضيا ، يتم تمثيل مؤشر جيني بـ

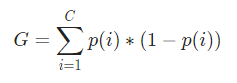
يعمل مؤشر جيني على المتغيرات الفئوية ويعطي النتائج من حيث "النجاح" أو "الفشل" وبالتالي يؤدي فقط الانقسام الثنائي. إنه ليس مكثفًا من الناحية الحسابية مثل نظيره - كسب المعلومات. من فهرس Gini ، يتم حساب قيمة معلمة أخرى تسمى Gini Gain والتي يتم تكبير قيمتها مع كل تكرار بواسطة Decision Tree للحصول على CART المثالي

دعونا نفهم حساب مؤشر جيني بمثال بسيط. في هذا ، لدينا إجمالي 10 نقاط بيانات بمتغيرين ، الأحمر والأزرق. تم ترقيم المحورين X و Y بمسافات من 100 بين كل مصطلح. من المثال المعطى ، يجب أن نحسب مؤشر جيني وكسب جيني.

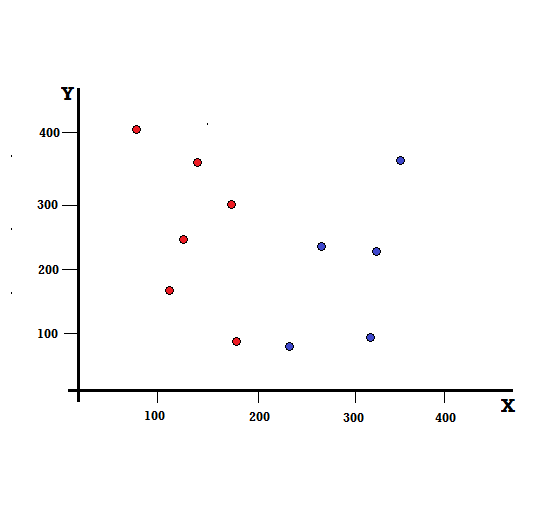
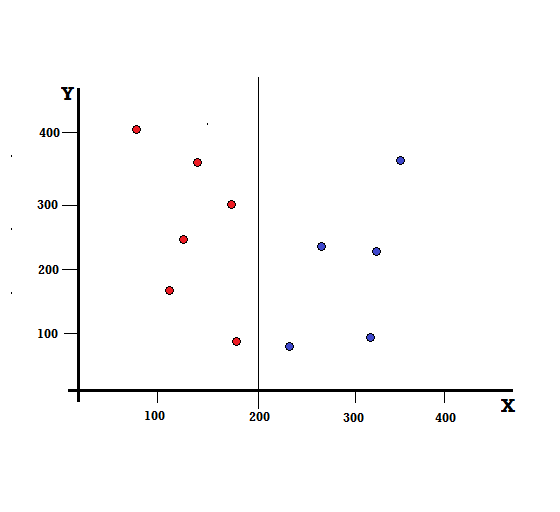
بالنسبة لشجرة القرار ، نحتاج إلى تقسيم مجموعة البيانات إلى فرعين. ضع في اعتبارك نقاط البيانات التالية مع تمييز 5 Reds و 5 Blues على مستوى XY. لنفترض أننا قمنا بعمل انقسام ثنائي عند X = 200 ، فسنحصل على انقسام كامل كما هو موضح أدناه.

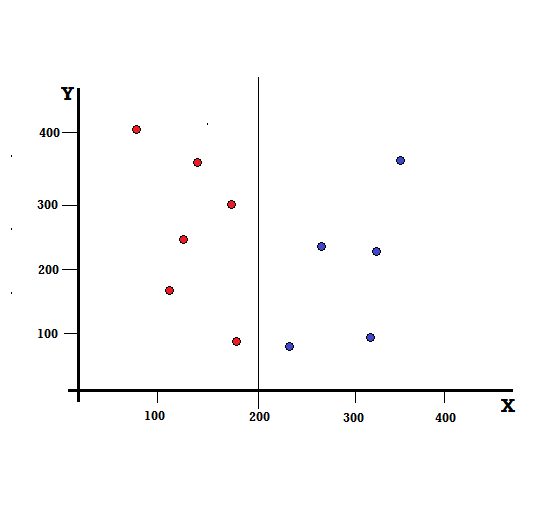
من الملاحظ أن الانقسام يتم بشكل صحيح ويبقى لدينا فرعين لكل منهما 5 درجات حمراء (الفرع الأيسر) و 5 البلوز (الفرع الأيمن).

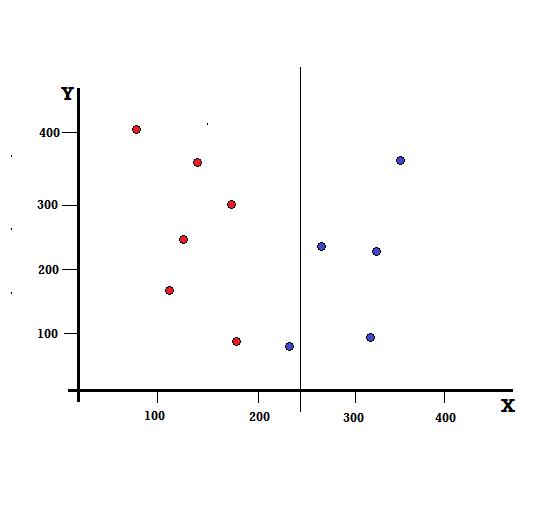
ولكن ماذا ستكون النتيجة إذا أجرينا الانقسام عند X = 250؟

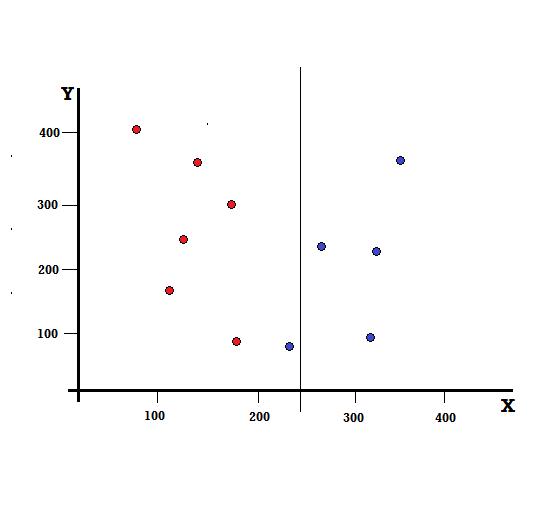
لقد تركنا مع فرعين ، الفرع الأيسر يتكون من 5 درجات حمراء و 1 أزرق ، بينما يتكون الفرع الأيمن من 4 بلوز. يشار إلى ما يلي على أنه انقسام غير كامل. في تدريب نموذج شجرة القرار ، لتحديد مقدار النقص في الانقسام ، يمكننا استخدام مؤشر جيني.

الخروج: أنواع الشجرة الثنائية

آلية أساسية

لحساب شائبة جيني ، دعونا أولاً نفهم آليتها الأساسية.

• أولاً ، سنختار عشوائيًا أي نقطة بيانات من مجموعة البيانات
• بعد ذلك ، سنقوم بتصنيفه عشوائيًا وفقًا لتوزيع الفئات في مجموعة البيانات المحددة. في مجموعة البيانات الخاصة بنا ، سنقدم نقطة بيانات مختارة باحتمال 5/10 للأحمر و 5/10 للأزرق حيث توجد خمس نقاط بيانات لكل لون ومن ثم الاحتمال.

الآن ، من أجل حساب مؤشر جيني ، يتم إعطاء الصيغة بواسطة

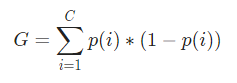
حيث C هو العدد الإجمالي للفئات و p ( i ) هو احتمال انتقاء نقطة البيانات مع الفئة i.

في المثال أعلاه ، لدينا C = 2 و p (1) = p (2) = 0.5 ، ومن ثم يمكن حساب مؤشر جيني على النحو التالي ،

G = ع (1) ∗ (1 / ف (1)) + ص (2) ∗ (1 / ف (2))

= 0.5 ∗ (1−0.5) + 0.5 ( 1−0.5 )

= 0.5

حيث 0.5 هو الاحتمال الإجمالي لتصنيف نقطة بيانات بشكل ناقص وبالتالي هو بالضبط 50٪.

الآن ، دعونا نحسب شائبة جيني لكل من الانقسام المثالي وغير الكامل الذي أجريناه سابقًا ،

انقسام مثالي

الفرع الأيسر يحتوي فقط على اللون الأحمر ، وبالتالي فإن جيني Impurity هو ،

G (يسار) = 1 ( 1−1) + 0 ( 1−0) = 0

يحتوي الفرع الأيمن أيضًا على موسيقى البلوز فقط ، ومن ثم يتم تقديم Gini Impurity أيضًا بواسطة ،

G (يمين) = 1 ( 1−1) + 0 ( 1−0) = 0

من الحساب السريع ، نرى أن كلا الفرعين الأيمن والأيسر من الانقسام الكامل لدينا احتمالية تساوي 0 ، وبالتالي فهي مثالية بالفعل. شوائب جيني 0 هي أقل شوائب ممكنة وأفضلها لأي مجموعة بيانات.

انقسام غير كامل

في هذه الحالة ، يحتوي الفرع الأيسر على 5 درجات حمراء و 1 أزرق. يمكن إعطاء النجاسة جيني من خلال ،

G (يسار) = 1/6 (1−1 / 6) + 5/6 ∗ (1−5 / 6) = 0.278

الفرع الأيمن لديه كل البلوز ، وبالتالي كما هو محسوب أعلاه Gini Impurity يتم تقديمه بواسطة ،

G (يمين) = 1 ( 1−1) + 0 ( 1−0) = 0

الآن بعد أن أصبح لدينا شوائب جيني للتقسيم غير الكامل ، من أجل تقييم جودة أو مدى الانقسام ، سنعطي وزناً محدداً لشوائب كل فرع مع عدد العناصر الموجودة به.

(0.6 ∗ 0.278) + (0.4 0) = 0.167

الآن بعد أن حسبنا مؤشر جيني ، سنقوم بحساب قيمة معامل آخر ، Gini Gain ونحلل تطبيقه في Decision Trees. يتم حساب مقدار الشوائب التي تمت إزالتها باستخدام هذا الانقسام عن طريق خصم القيمة أعلاه باستخدام مؤشر جيني لمجموعة البيانات بأكملها (0.5)

0.5 - 0.167 = 0.333

تسمى هذه القيمة المحسوبة باسم " Gini Gain ". بعبارات بسيطة ، ربح جيني الأعلى = انقسام أفضل .

ومن ثم ، في خوارزمية شجرة القرار ، يتم الحصول على أفضل تقسيم عن طريق تعظيم كسب جيني ، والذي يتم حسابه بالطريقة المذكورة أعلاه مع كل تكرار.

بعد حساب Gini Gain لكل سمة في مجموعة البيانات ، سيختار الفصل sklearn.tree.DecisionTreeClassifier أكبر Gini Gain كعقدة الجذر. عندما يتم مواجهة فرع مع جيني 0 ، فإنه يصبح عقدة الورقة وتحتاج الفروع الأخرى التي تحتوي على جيني أكثر من 0 إلى مزيد من الانقسام. تتم زراعة هذه العقد بشكل متكرر حتى يتم تصنيفها جميعًا.

استخدم في تعلم الآلة

هناك العديد من الخوارزميات المصممة لأغراض مختلفة في عالم التعلم الآلي. تكمن المشكلة في تحديد الخوارزمية الأنسب لمجموعة بيانات معينة. يبدو أن خوارزمية شجرة القرار تظهر نتائج مقنعة أيضًا. للتعرف عليه ، يجب أن يعتقد المرء أن أشجار القرار تحاكي إلى حد ما القوة الذاتية البشرية.

لذلك ، من المرجح أن تكون المشكلة مع المزيد من الأسئلة المعرفية البشرية أكثر ملاءمة لأشجار القرار. يمكن فهم المفهوم الأساسي لأشجار القرار بسهولة بسبب هيكلها الشبيه بالأشجار.

اقرأ أيضًا: شجرة القرار في الذكاء الاصطناعي: مقدمة ، أنواع ، وخلق

خاتمة

بديل لمؤشر جيني هو إنتروبيا المعلومات التي تستخدم لتحديد السمة التي تعطينا أقصى قدر من المعلومات حول الفصل. يقوم على مفهوم الانتروبيا ، وهي درجة الشوائب أو عدم اليقين. يهدف إلى تقليل مستوى الانتروبيا من العقد الجذرية إلى العقد الورقية لشجرة القرار.

بهذه الطريقة ، يتم استخدام مؤشر جيني بواسطة خوارزميات CART لتحسين أشجار القرار وإنشاء نقاط قرار لأشجار التصنيف.

إذا كنت مهتمًا بمعرفة المزيد حول التعلم الآلي ، فراجع دبلوم PG في IIIT-B & upGrad في التعلم الآلي والذكاء الاصطناعي المصمم للمهنيين العاملين ويقدم أكثر من 450 ساعة من التدريب الصارم ، وأكثر من 30 دراسة حالة ومهمة ، IIIT- حالة الخريجين B ، أكثر من 5 مشاريع تتويجا عملية ومساعدة وظيفية مع أفضل الشركات.