Indice Gini per alberi decisionali: meccanismo, divisione perfetta e imperfetta con esempi

introduzione

Decision Tree è uno degli approcci pratici più comunemente usati per l'apprendimento supervisionato. Può essere utilizzato per risolvere sia le attività di regressione che di classificazione, con quest'ultima più in pratica. In questi alberi, le etichette di classe sono rappresentate dalle foglie ei rami denotano le congiunzioni di caratteristiche che portano a quelle etichette di classe. È ampiamente utilizzato negli algoritmi di apprendimento automatico. In genere, un approccio di apprendimento automatico include il controllo di molti iperparametri e ottimizzazioni.

L'albero di regressione viene utilizzato quando il risultato previsto è un numero reale e l'albero di classificazione viene utilizzato per prevedere la classe a cui appartengono i dati. Questi due termini sono chiamati collettivamente come Classification and Regression Trees (CART).

Si tratta di tecniche di apprendimento dell'albero decisionale non parametrico che forniscono alberi di regressione o classificazione, a seconda che la variabile dipendente sia rispettivamente categoriale o numerica. Questo algoritmo implementa il metodo di Gini Index per originare divisioni binarie. Sia Gini Index che Gini Impurity sono usati in modo intercambiabile.

Gli alberi decisionali hanno influenzato i modelli di regressione nell'apprendimento automatico. Durante la progettazione dell'albero, gli sviluppatori impostano le caratteristiche dei nodi e i possibili attributi di tale caratteristica con i bordi.

Calcolo

Il Gini Index o Gini Impurity si calcola sottraendo da una la somma delle probabilità al quadrato di ciascuna classe. Predilige principalmente le partizioni più grandi e sono molto semplici da implementare. In parole povere, calcola la probabilità che una certa caratteristica selezionata casualmente sia stata classificata in modo errato.

L'indice di Gini varia tra 0 e 1, dove 0 rappresenta la purezza della classificazione e 1 denota la distribuzione casuale degli elementi tra le varie classi. Un indice Gini di 0,5 mostra che esiste un'equa distribuzione degli elementi in alcune classi.

Matematicamente, l'indice di Gini è rappresentato da

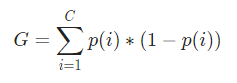
L'indice Gini lavora su variabili categoriali e fornisce i risultati in termini di "successo" o "fallimento" e quindi esegue solo la divisione binaria. Non è computazionalmente intensivo come la sua controparte: Information Gain. Dal Gini Index viene calcolato il valore di un altro parametro chiamato Gini Gain il cui valore viene massimizzato ad ogni iterazione dal Decision Tree per ottenere il CART perfetto

Cerchiamo di capire il calcolo dell'Indice Gini con un semplice esempio. In questo, abbiamo un totale di 10 punti dati con due variabili, i rossi e i blu. Gli assi X e Y sono numerati con spazi di 100 tra ogni termine. Dall'esempio fornito, calcoleremo l'Indice Gini e il Gini Gain.

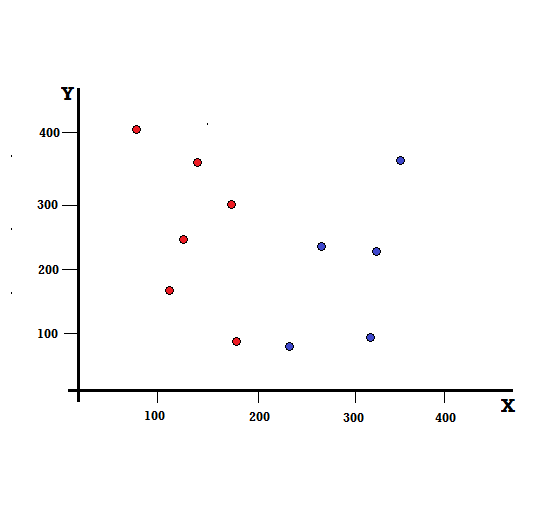
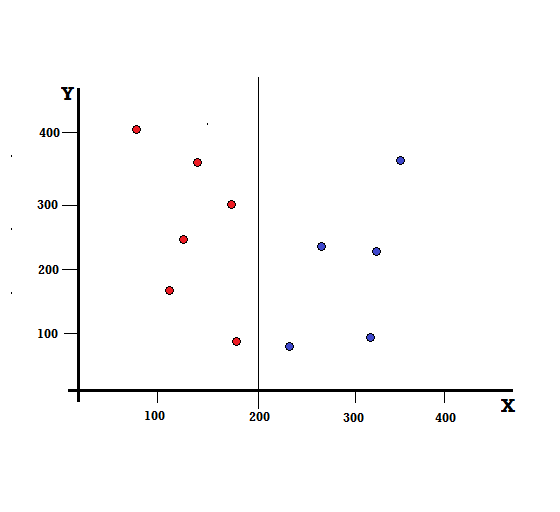
Per un albero decisionale, dobbiamo dividere il set di dati in due rami. Considera i seguenti punti dati con 5 rossi e 5 blu contrassegnati sul piano XY. Supponiamo di fare una divisione binaria a X=200, quindi avremo una divisione perfetta come mostrato di seguito.

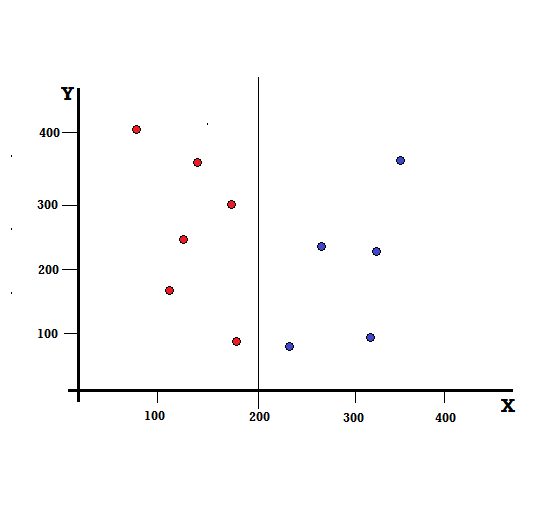
Si vede che lo split viene eseguito correttamente e ci rimangono due rami ciascuno con 5 rossi (ramo di sinistra) e 5 blu (ramo di destra).

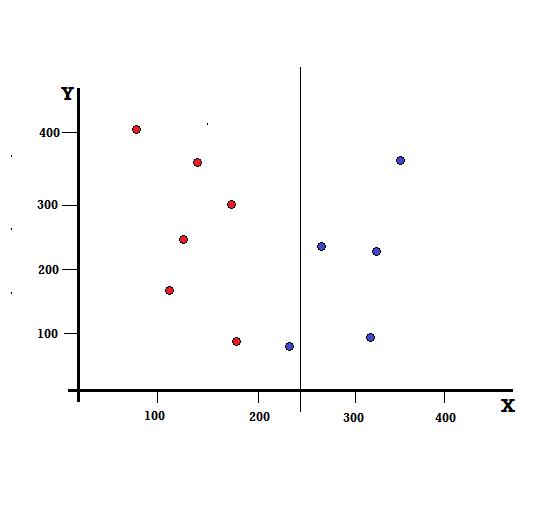
Ma quale sarà il risultato se facciamo la divisione a X=250?

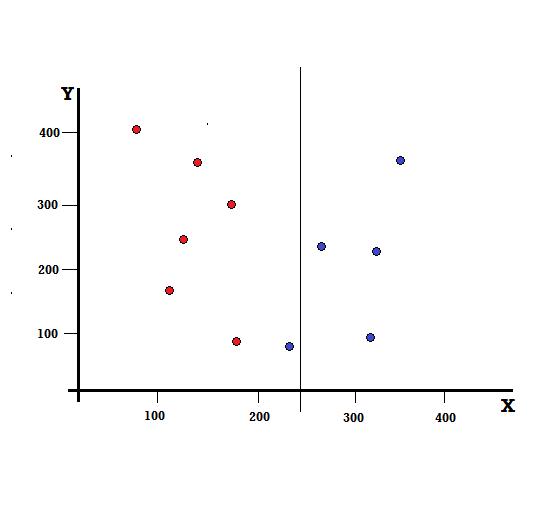
Ci rimangono due rami, il ramo sinistro composto da 5 rossi e 1 blu, mentre il ramo destro è composto da 4 blu. Quanto segue è indicato come una divisione imperfetta. Nell'allenamento del modello Decision Tree, per quantificare la quantità di imperfezione della divisione, possiamo utilizzare l'indice di Gini.

Checkout: tipi di albero binario

Meccanismo di base

Per calcolare la Gini Impurity , cerchiamo innanzitutto di capire il suo meccanismo di base.

• Innanzitutto, raccoglieremo casualmente qualsiasi punto dati dal set di dati
• Quindi, lo classificheremo in modo casuale in base alla distribuzione delle classi nel set di dati fornito. Nel nostro set di dati, forniremo un punto dati scelto con una probabilità di 5/10 per il rosso e 5/10 per il blu poiché ci sono cinque punti dati di ciascun colore e quindi la probabilità.

Ora, per calcolare l'Indice di Gini, la formula è data da

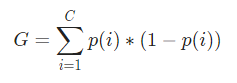
Dove C è il numero totale di classi e p( i ) è la probabilità di selezionare il punto dati con la classe i.

Nell'esempio sopra, abbiamo C=2 e p(1) = p(2) = 0,5, quindi l'indice di Gini può essere calcolato come,

G =p(1) ∗ (1−p(1)) + p(2) ∗ (1−p(2))

=0,5 ∗ (1−0,5) + 0,5 ∗ (1−0,5)

=0,5

Dove 0,5 è la probabilità totale di classificare un punto dati in modo imperfetto e quindi è esattamente il 50%.

Ora, calcoliamo l'impurità di Gini sia per la divisione perfetta che per quella imperfetta che abbiamo eseguito in precedenza,

Spaccatura perfetta

Il ramo sinistro ha solo rossi e quindi la sua Gini Impurity è,

G(sinistra) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Anche il ramo destro ha solo blues e quindi la sua Gini Impurity è data anche da,

G(destra) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Dal rapido calcolo, vediamo che entrambi i rami sinistro e destro della nostra divisione perfetta hanno probabilità pari a 0 e quindi sono davvero perfetti. Un'impurità Gini di 0 è l'impurità più bassa e migliore possibile per qualsiasi set di dati.

Spaccatura imperfetta

In questo caso, il ramo sinistro ha 5 rossi e 1 blu. La sua Impurità Gini può essere data da,

G(sinistra) =1/6 ∗ (1−1/6) + 5/6 ∗ (1−5/6) = 0,278

Il ramo di destra ha tutti i blues e quindi come calcolato sopra la sua Gini Impurity è data da,

G(destra) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Ora che abbiamo le Impurezze di Gini della scissione imperfetta, per valutare la qualità o l'entità della scissione, daremo un peso specifico all'impurità di ogni ramo con il numero di elementi che ha.

(0,6 ∗ 0,278) + (0,4 ∗ 0) = 0,167

Ora che abbiamo calcolato il Gini Index, calcoleremo il valore di un altro parametro, Gini Gain, e analizzeremo la sua applicazione in Decision Trees. La quantità di impurità rimossa con questa suddivisione viene calcolata sottraendo il valore sopra con l'indice Gini per l'intero set di dati (0,5)

0,5 – 0,167 = 0,333

Questo valore calcolato è chiamato “ Gini Gain ”. In parole povere, Gini Gain più alto = Better Split .

Quindi, in un algoritmo Decision Tree, la divisione migliore si ottiene massimizzando il Gini Gain, che viene calcolato nel modo sopra ad ogni iterazione.

Dopo aver calcolato il Gini Gain per ogni attributo nel set di dati, la classe, sklearn.tree.DecisionTreeClassifier sceglierà il più grande Gini Gain come nodo radice. Quando si incontra un ramo con Gini di 0, diventa il nodo foglia e gli altri rami con Gini maggiore di 0 necessitano di un'ulteriore suddivisione. Questi nodi vengono cresciuti in modo ricorsivo fino a quando non vengono classificati tutti.

Utilizzare nell'apprendimento automatico

Esistono vari algoritmi progettati per scopi diversi nel mondo del machine learning. Il problema sta nell'identificare quale algoritmo si adatta meglio a un dato set di dati. Anche l'algoritmo dell'albero decisionale sembra mostrare risultati convincenti. Per riconoscerlo, si deve pensare che gli alberi decisionali imitano in qualche modo il potere soggettivo umano.

Quindi, è probabile che un problema con più domande cognitive umane sia più adatto per gli alberi decisionali. Il concetto alla base degli alberi decisionali può essere facilmente comprensibile per la sua struttura ad albero.

Leggi anche: Decision Tree in AI: Introduzione, Tipi e Creazione

Conclusione

Un'alternativa all'Indice Gini è l'Information Entropy, utilizzato per determinare quale attributo ci fornisce la massima informazione su una classe. Si basa sul concetto di entropia, che è il grado di impurità o incertezza. Mira a diminuire il livello di entropia dai nodi radice ai nodi foglia dell'albero decisionale.

In questo modo, l'Indice Gini viene utilizzato dagli algoritmi CART per ottimizzare gli alberi decisionali e creare punti di decisione per alberi di classificazione.

Se sei interessato a saperne di più sull'apprendimento automatico, dai un'occhiata al Diploma PG di IIIT-B e upGrad in Machine Learning e AI, progettato per i professionisti che lavorano e offre oltre 450 ore di formazione rigorosa, oltre 30 casi di studio e incarichi, IIIT- B Status di Alumni, oltre 5 progetti pratici pratici e assistenza sul lavoro con le migliori aziende.