ดัชนีจินีสำหรับแผนผังการตัดสินใจ: กลไก การแยกส่วนที่สมบูรณ์แบบและไม่สมบูรณ์พร้อมตัวอย่าง

บทนำ

Decision Tree เป็นหนึ่งในแนวทางปฏิบัติที่ใช้บ่อยที่สุดสำหรับการเรียนรู้ภายใต้การดูแล สามารถใช้ในการแก้ปัญหาทั้งงานการถดถอยและการจำแนกประเภทโดยที่ส่วนหลังถูกนำไปใช้จริงมากขึ้น ในต้นไม้เหล่านี้ ป้ายชื่อคลาสจะแสดงด้วยใบไม้ และกิ่งก้านแสดงถึงการรวมตัวของคุณสมบัติที่นำไปสู่ป้ายชื่อคลาสเหล่านั้น มีการใช้กันอย่างแพร่หลายในอัลกอริธึมการเรียนรู้ของเครื่อง โดยทั่วไป วิธีการเรียนรู้ของเครื่องจะรวมถึงการควบคุมไฮเปอร์พารามิเตอร์และการเพิ่มประสิทธิภาพจำนวนมาก

ต้นไม้การถดถอยจะใช้เมื่อผลลัพธ์ที่คาดการณ์ไว้เป็นจำนวนจริง และใช้แผนผังการจำแนกประเภทเพื่อทำนายคลาสของข้อมูล คำศัพท์สองคำนี้เรียกรวมกันว่า ต้นไม้การจำแนกและการถดถอย (CART)

เหล่านี้เป็นเทคนิคการเรียนรู้แผนภูมิการตัดสินใจแบบไม่อิงพารามิเตอร์ที่ให้แผนภูมิการถดถอยหรือการจัดหมวดหมู่โดยขึ้นอยู่กับว่าตัวแปรตามนั้นเป็นหมวดหมู่หรือตัวเลขตามลำดับ อัลกอริทึมนี้ปรับใช้วิธีการของ Gini Index เพื่อเริ่มต้นการแยกไบนารี ทั้ง Gini Index และ Gini Impurity ใช้แทนกันได้

แผนผังการตัดสินใจมีอิทธิพลต่อโมเดลการถดถอยในการเรียนรู้ของเครื่อง ขณะออกแบบแผนผัง นักพัฒนาจะตั้งค่าคุณสมบัติของโหนดและแอตทริบิวต์ที่เป็นไปได้ของฟีเจอร์นั้นด้วยขอบ

การคำนวณ

ดัชนีจินีหรือจินีเจือปนคำนวณโดยการลบผลรวมของความน่าจะเป็นยกกำลังสองของแต่ละคลาสออกจากหนึ่ง ส่วนใหญ่จะสนับสนุนพาร์ติชั่นที่ใหญ่กว่าและง่ายต่อการติดตั้ง ในแง่ง่ายๆ จะคำนวณความน่าจะเป็นของคุณลักษณะที่เลือกแบบสุ่มบางรายการซึ่งจัดประเภทไม่ถูกต้อง

ดัชนีจินีจะแปรผันระหว่าง 0 ถึง 1 โดยที่ 0 หมายถึงความบริสุทธิ์ของการจัดประเภท และ 1 หมายถึงการแจกแจงองค์ประกอบแบบสุ่มในคลาสต่างๆ ดัชนี Gini ที่ 0.5 แสดงว่ามีการกระจายองค์ประกอบที่เท่าเทียมกันในบางคลาส

ทางคณิตศาสตร์ ดัชนีจินี ถูกแทนด้วย

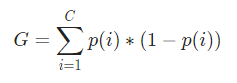
ดัชนี Gini ทำงานกับตัวแปรตามหมวดหมู่และให้ผลลัพธ์ในแง่ของ "ความสำเร็จ" หรือ "ความล้มเหลว" และด้วยเหตุนี้จึงดำเนินการแยกไบนารีเท่านั้น ไม่ได้ใช้การคำนวณอย่างเข้มข้นเหมือนคู่กัน – Information Gain จากดัชนี Gini ค่าของพารามิเตอร์อื่นที่ชื่อ Gini Gain จะถูกคำนวณซึ่งค่าจะถูกขยายให้ใหญ่สุดด้วยการวนซ้ำแต่ละครั้งโดย Decision Tree เพื่อให้ได้ CART ที่สมบูรณ์แบบ

ให้เราเข้าใจการคำนวณดัชนี Gini ด้วยตัวอย่างง่ายๆ ในที่นี้ เรามีจุดข้อมูลทั้งหมด 10 จุดซึ่งมีสองตัวแปร ได้แก่ สีแดงและสีน้ำเงิน แกน X และ Y ถูกนับด้วยช่องว่าง 100 ระหว่างแต่ละเทอม จากตัวอย่างที่ให้มา เราจะคำนวณ Gini Index และ Gini Gain

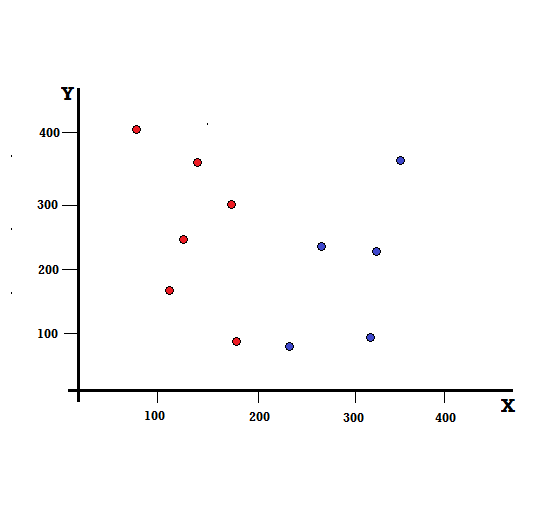
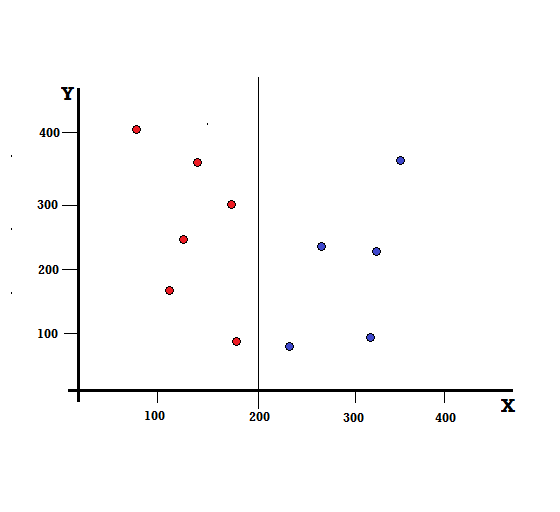
สำหรับแผนผังการตัดสินใจ เราต้องแยกชุดข้อมูลออกเป็นสองสาขา พิจารณาจุดข้อมูลต่อไปนี้ด้วยเครื่องหมาย 5 สีแดงและ 5 สีน้ำเงินบนระนาบ XY สมมติว่าเราทำการแยกไบนารีที่ X=200 จากนั้นเราจะมีการแยกที่สมบูรณ์แบบดังที่แสดงด้านล่าง

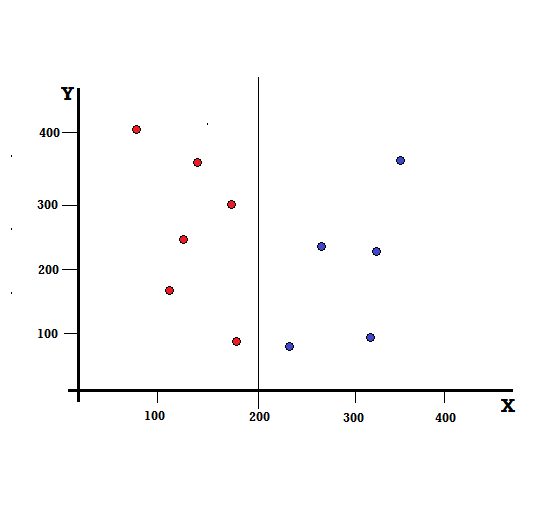
จะเห็นได้ว่าการแบ่งได้ถูกต้องและเราเหลือสองกิ่งก้านละ 5 สีแดง (กิ่งซ้าย) และ 5 สีน้ำเงิน (กิ่งขวา)

แต่ผลลัพธ์จะเป็นอย่างไรถ้าเราทำการแยกที่ X=250?

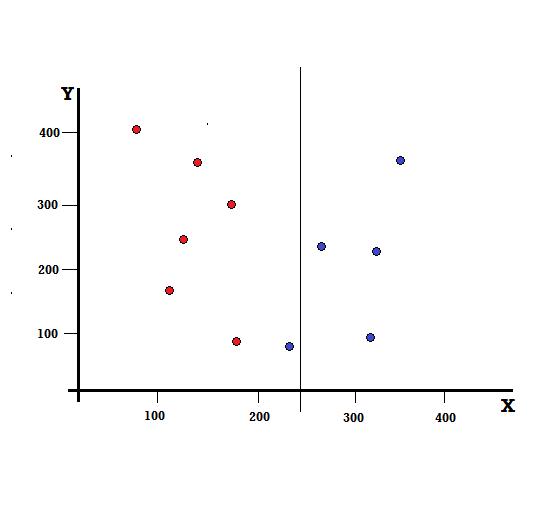
เหลือสองกิ่ง กิ่งซ้ายมีสีแดง 5 อัน และสีน้ำเงิน 1 อัน กิ่งขวาประกอบด้วยบลูส์ 4 อัน ต่อไปนี้เรียกว่าการแยกที่ไม่สมบูรณ์ ในการฝึกโมเดล Decision Tree เพื่อหาปริมาณความไม่สมบูรณ์ของการแยก เราสามารถใช้ดัชนี Gini

ชำระเงิน: ประเภทของไบนารีทรี

กลไกพื้นฐาน

ในการคำนวณสิ่งเจือปน Gini ให้ เราเข้าใจกลไกพื้นฐานก่อน

• อันดับแรก เราจะสุ่มเลือกจุดข้อมูลใดๆ จากชุดข้อมูล
• จากนั้นเราจะจัดประเภทแบบสุ่มตามการแจกแจงคลาสในชุดข้อมูลที่กำหนด ในชุดข้อมูลของเรา เราจะให้จุดข้อมูลที่เลือกด้วยความน่าจะเป็น 5/10 สำหรับสีแดง และ 5/10 สำหรับสีน้ำเงิน เนื่องจากมีจุดข้อมูลห้าจุดสำหรับแต่ละสี และความน่าจะเป็น

ทีนี้ ในการคำนวณดัชนีจินี จะได้สูตรโดย

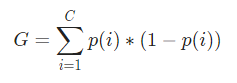
โดยที่ C คือจำนวนคลาสทั้งหมดและ p( i ) คือความน่าจะเป็นของการเลือกจุดข้อมูลด้วยคลาส i

ในตัวอย่างข้างต้น เรามี C=2 และ p(1) = p(2) = 0.5 ดังนั้น ดัชนี Gini สามารถคำนวณได้ดังนี้

G =p(1) ∗ (1−p(1)) + p(2) ∗ (1−p(2))

=0.5 ∗ (1−0.5) + 0.5 ∗ (1−0.5)

=0.5

โดยที่ 0.5 คือความน่าจะเป็นรวมของการจำแนกจุดข้อมูลอย่างไม่สมบูรณ์ ดังนั้นจึงเท่ากับ 50% พอดี

ตอนนี้ ให้เราคำนวณ Gini Impurity สำหรับการแยกที่สมบูรณ์แบบและไม่สมบูรณ์ที่เราดำเนินการก่อนหน้านี้

การแยกที่สมบูรณ์แบบ

กิ่งด้านซ้ายมีเพียงสีแดง ดังนั้น Gini Impurity ของมันคือ

G(ซ้าย) =1 ∗ (1-1) + 0 ∗ (1−0) = 0

แบรนช์ด้านขวายังมีเพียงบลูส์และด้วยเหตุนี้ Gini Impurity จึงได้รับจาก

G(ขวา) =1 ∗ (1-1) + 0 ∗ (1−0) = 0

จากการคำนวณอย่างรวดเร็ว เราจะเห็นว่าทั้งกิ่งซ้ายและขวาของการแยกที่สมบูรณ์แบบของเรามีความน่าจะเป็นเป็น 0 และด้วยเหตุนี้จึงสมบูรณ์แบบอย่างแท้จริง Gini Impurity เท่ากับ 0 คือค่าต่ำสุดและสิ่งสกปรกที่ดีที่สุดสำหรับชุดข้อมูลใดๆ

การแยกที่ไม่สมบูรณ์

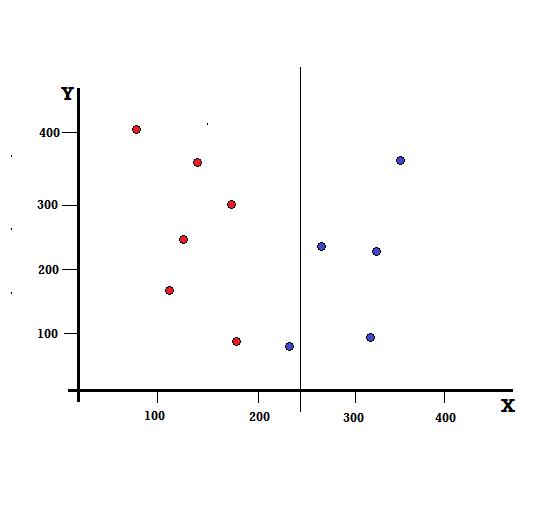
ในกรณีนี้ กิ่งซ้ายมี 5 สีแดงและ 1 สีน้ำเงิน สามารถให้สิ่งเจือปนของ Gini ได้โดย

G(ซ้าย) =1/6 ∗ (1-1/6) + 5/6 ∗ (1-5/6) = 0.278

แบรนช์ด้านขวามีบลูส์ทั้งหมดและด้วยเหตุนี้ตามที่คำนวณเหนือเจนี่เจือปนจะได้มาจาก

G(ขวา) =1 ∗ (1-1) + 0 ∗ (1−0) = 0

ตอนนี้เรามีจินีเจือปนของรอยแยกที่ไม่สมบูรณ์ เพื่อประเมินคุณภาพหรือขอบเขตของการแยก เราจะให้น้ำหนักเฉพาะกับสิ่งเจือปนของแต่ละกิ่งด้วยจำนวนองค์ประกอบที่มี

(0.6 ∗ 0.278) + (0.4 ∗ 0) = 0.167

ตอนนี้เราได้คำนวณดัชนี Gini แล้ว เราจะคำนวณค่าของพารามิเตอร์อื่น Gini Gain และวิเคราะห์การใช้งานใน Decision Trees ปริมาณสิ่งเจือปนที่ถูกกำจัดด้วยการแยกนี้คำนวณโดยการหักค่าข้างต้นด้วยดัชนี Gini สำหรับชุดข้อมูลทั้งหมด (0.5)

0.5 – 0.167 = 0.333

ค่าที่คำนวณได้นี้เรียกว่า “ Gini Gain ” ในแง่ง่ายๆ Gini Gain ที่สูงขึ้น = Better Split

ดังนั้น ในอัลกอริธึมแผนผังการตัดสินใจ การแบ่งที่ดีที่สุดจะได้มาจากการเพิ่ม Gini Gain สูงสุด ซึ่งคำนวณในลักษณะข้างต้นด้วยการวนซ้ำแต่ละครั้ง

หลังจากคำนวณ Gini Gain สำหรับแต่ละแอตทริบิวต์ในชุดข้อมูลแล้ว คลาส sklearn.tree.DecisionTreeClassifier จะเลือก Gini Gain ที่ใหญ่ที่สุดเป็น Root Node เมื่อพบสาขาที่มี Gini เป็น 0 มันจะกลายเป็นโหนดปลายสุดและสาขาอื่นที่มี Gini มากกว่า 0 จำเป็นต้องแยกกันเพิ่มเติม โหนดเหล่านี้จะเติบโตแบบเรียกซ้ำจนกว่าจะจัดประเภททั้งหมด

ใช้ในการเรียนรู้ของเครื่อง

มีอัลกอริทึมต่างๆ ที่ออกแบบมาเพื่อวัตถุประสงค์ที่แตกต่างกันในโลกของการเรียนรู้ของเครื่อง ปัญหาอยู่ที่การระบุอัลกอริทึมที่เหมาะสมที่สุดกับชุดข้อมูลที่กำหนด อัลกอริธึมแผนผังการตัดสินใจดูเหมือนจะแสดงผลที่น่าเชื่อเช่นกัน เราต้องคิดว่าต้นไม้ตัดสินใจค่อนข้างเลียนแบบอำนาจอัตนัยของมนุษย์

ดังนั้น ปัญหาเกี่ยวกับการตั้งคำถามเกี่ยวกับความรู้ความเข้าใจของมนุษย์จึงมีแนวโน้มว่าจะเหมาะสมกว่าสำหรับแผนภูมิต้นไม้การตัดสินใจ แนวคิดพื้นฐานของแผนผังการตัดสินใจสามารถเข้าใจได้ง่ายสำหรับโครงสร้างที่เหมือนต้นไม้

อ่านเพิ่มเติม: โครงสร้างการตัดสินใจใน AI: บทนำ ประเภท & การสร้าง

บทสรุป

อีกทางเลือกหนึ่งสำหรับดัชนี Gini คือ Information Entropy ซึ่งใช้ในการพิจารณาว่าแอตทริบิวต์ใดให้ข้อมูลสูงสุดเกี่ยวกับชั้นเรียนแก่เรา มันขึ้นอยู่กับแนวคิดของเอนโทรปีซึ่งเป็นระดับของสิ่งเจือปนหรือความไม่แน่นอน มีจุดมุ่งหมายเพื่อลดระดับของเอนโทรปีจากโหนดรูทไปยังโหนดลีฟของแผนผังการตัดสินใจ

ด้วยวิธีนี้ ดัชนี Gini ถูกใช้โดยอัลกอริธึม CART เพื่อปรับโครงสร้างการตัดสินใจให้เหมาะสมและสร้างจุดตัดสินใจสำหรับแผนผังการจำแนกประเภท

หากคุณสนใจที่จะเรียนรู้เพิ่มเติมเกี่ยวกับแมชชีนเลิร์นนิง โปรดดูที่ IIIT-B & upGrad's PG Diploma in Machine Learning & AI ซึ่งออกแบบมาสำหรับมืออาชีพที่ทำงานและมีการฝึกอบรมที่เข้มงวดมากกว่า 450 ชั่วโมง กรณีศึกษาและการมอบหมายมากกว่า 30 รายการ IIIT- สถานะศิษย์เก่า B, 5+ โครงการหลักที่ใช้งานได้จริง & ความช่วยเหลือด้านงานกับบริษัทชั้นนำ