決策樹的基尼指數：機制，完美和不完美的拆分示例

介紹

決策樹是監督學習中最常用的實用方法之一。 它可用於解決回歸和分類任務，後者更多地投入實際應用。 在這些樹中，類標籤由葉子表示，分支表示導致這些類標籤的特徵的結合。 它廣泛用於機器學習算法。 通常，機器學習方法包括控制許多超參數和優化。

當預測結果為實數時使用回歸樹，分類樹用於預測數據所屬的類別。 這兩個術語統稱為分類和回歸樹 (CART)。

這些是提供回歸或分類樹的非參數決策樹學習技術，分別取決於因變量是分類變量還是數值變量。 該算法採用基尼指數的方法來發起二元分裂。 基尼指數和基尼雜質可以互換使用。

決策樹影響了機器學習中的回歸模型。 在設計樹時，開發人員使用邊設置節點的特徵和該特徵的可能屬性。

計算

基尼指數或基尼雜質是通過從 1 中減去每個類別的概率平方和來計算的。 它主要支持較大的分區，並且實現起來非常簡單。 簡單來說，它計算某個隨機選擇的特徵被錯誤分類的概率。

基尼指數在 0 和 1 之間變化，其中 0 表示分類的純度，1 表示元素在各個類別中的隨機分佈。 基尼指數為 0.5 表明在某些類別中元素的分佈是相等的。

在數學上，基尼指數表示為

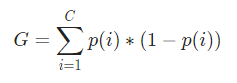
基尼指數適用於分類變量，並根據“成功”或“失敗”給出結果，因此只執行二元拆分。 它不像其對應的信息增益那樣計算密集。 根據基尼指數，計算另一個名為 Gini Gain 的參數的值，其值在決策樹的每次迭代中最大化，以獲得完美的 CART

讓我們通過一個簡單的例子來理解基尼指數的計算。 在這裡，我們總共有 10 個數據點，其中有兩個變量，紅色和藍色。 X 軸和 Y 軸以每項之間的 100 間隔編號。 從給定的例子中，我們將計算基尼指數和基尼增益。

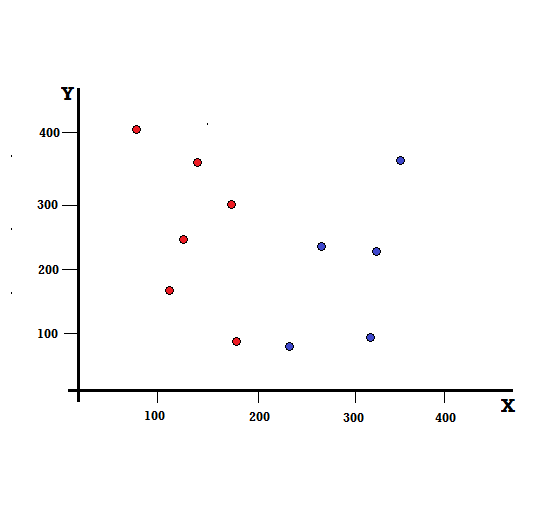
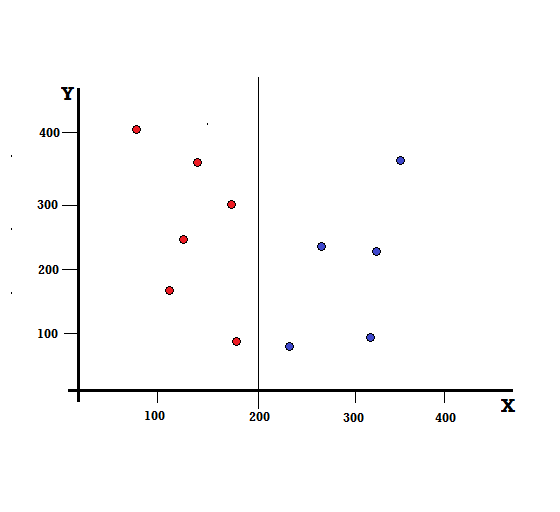
對於決策樹，我們需要將數據集分成兩個分支。 考慮以下在 XY 平面上標記了 5 個紅色和 5 個藍色的數據點。 假設我們在 X=200 處進行二元拆分，那麼我們將得到如下所示的完美拆分。

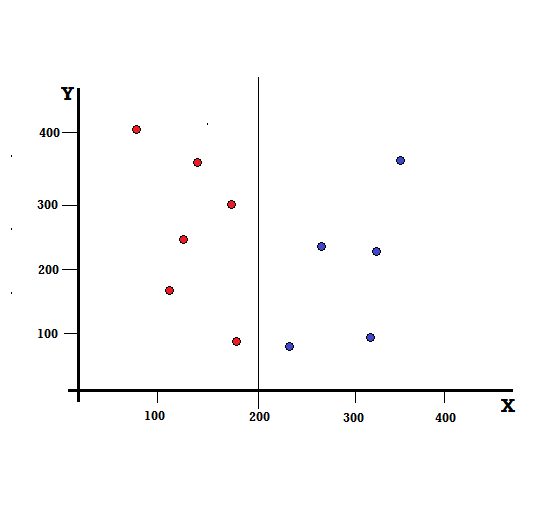
可以看出，拆分是正確執行的，我們剩下兩個分支，每個分支有 5 個紅色（左分支）和 5 個藍色（右分支）。

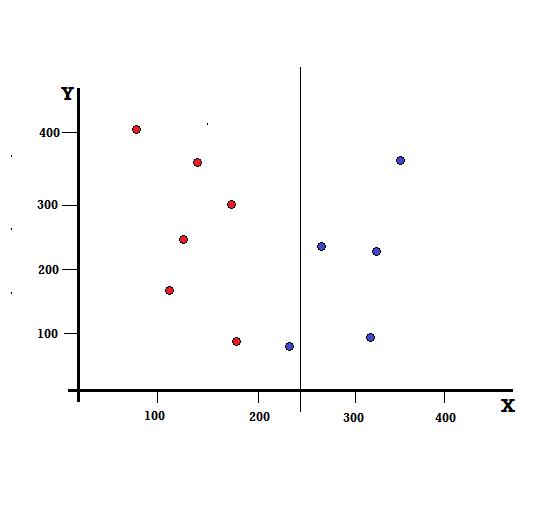
但是，如果我們在 X=250 處進行拆分，結果會是什麼？

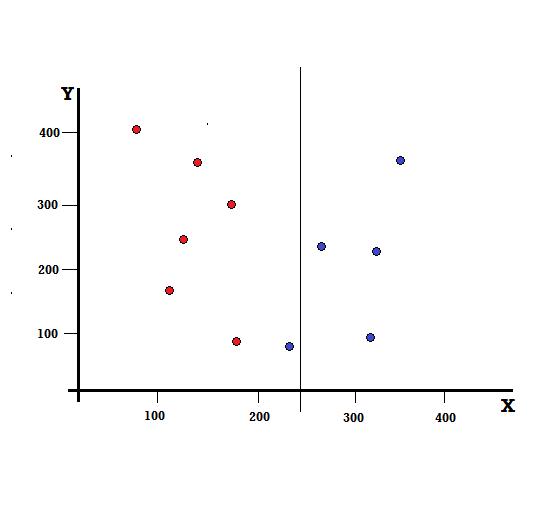
我們剩下兩個分支，左分支由 5 個紅色和 1 個藍色組成，而右分支由 4 個藍色組成。 以下稱為不完美分裂。 在訓練決策樹模型時，為了量化分裂的不完美程度，我們可以使用基尼指數。

結帳：二叉樹的類型

基本機制

計算基尼雜質，讓我們首先了解它的基本機制。

• 首先，我們將從數據集中隨機選取任何數據點
• 然後，我們將根據給定數據集中的類分佈對其進行隨機分類。 在我們的數據集中，我們將給出一個數據點，選擇紅色的概率為 5/10，藍色的概率為 5/10，因為每種顏色有五個數據點，因此概率。

現在，為了計算基尼指數，公式如下

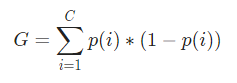
其中，C 是類的總數，p( i )​​ 是選擇具有類i 的數據點的概率。

在上面的例子中，我們有 C=2 和 p(1) = p(2) = 0.5，因此基尼指數可以計算為，

G =p(1) ∗ (1−p(1)) + p(2) ∗ (1−p(2))

=0.5 * (1−0.5) + 0.5 * (1−0.5)

=0.5

其中 0.5 是對數據點進行不完美分類的總概率，因此正好是 50%。

現在，讓我們計算我們之前執行的完美和不完美分割的基尼雜質，

完美分裂

左分支只有紅色，因此它的基尼雜質是，

G(左) =1 * (1−1) + 0 * (1−0) = 0

右支也只有布魯斯，因此它的基尼雜質也由下式給出，

G(右) =1 * (1−1) + 0 * (1−0) = 0

通過快速計算，我們看到完美分割的左右分支的概率均為 0，因此確實是完美的。 對於任何數據集，基尼雜質 0 是最低和最好的雜質。

不完美分裂

在這種情況下，左分支有 5 個紅色和 1 個藍色。 它的基尼雜質可以通過以下方式給出，

G(左) =1/6 * (1−1/6) + 5/6 * (1−5/6) = 0.278

右分支全部為藍色，因此如上計算，其基尼雜質由下式給出，

G(右) =1 * (1−1) + 0 * (1−0) = 0

既然我們有了不完美分裂的基尼雜質，為了評估分裂的質量或程度，我們將用它所具有的元素數量對每個分支的雜質賦予特定的權重。

(0.6 * 0.278) + (0.4 * 0) = 0.167

現在我們已經計算了基尼指數，我們將計算另一個參數的值，基尼增益並分析其在決策樹中的應用。 通過使用整個數據集的基尼指數（0.5）減去上述值來計算通過此拆分去除的雜質量

0.5 – 0.167 = 0.333

計算出的這個值稱為“基尼增益”。 簡單來說，更高的基尼增益 = 更好的分割。

因此，在決策樹算法中，通過最大化 Gini Gain 來獲得最佳分割，該 Gini Gain 是在每次迭代時以上述方式計算的。

在計算數據集中每個屬性的 Gini Gain 後，類 sklearn.tree.DecisionTreeClassifier 將選擇最大的 Gini Gain 作為 Root Node。 當遇到 Gini 為 0 的分支時，它將成為葉節點，而 Gini 大於 0 的其他分支需要進一步分裂。 這些節點遞歸地增長，直到它們都被分類。

在機器學習中使用

在機器學習的世界中，有多種算法針對不同的目的而設計。 問題在於確定哪種算法最適合給定數據集。 決策樹算法似乎也顯示出令人信服的結果。 要認識到這一點，人們必須認為決策樹在某種程度上模仿了人類的主觀能力。

因此，具有更多人類認知問題的問題可能更適合決策樹。 決策樹的基本概念因其樹狀結構而易於理解。

另請閱讀：人工智能中的決策樹：簡介、類型和創建

結論

基尼指數的替代方案是信息熵，它用於確定哪個屬性為我們提供了關於一個類的最大信息。 它基於熵的概念，熵是雜質或不確定性的程度。 它旨在降低從根節點到決策樹葉節點的熵水平。

通過這種方式，CART 算法使用基尼指數來優化決策樹並為分類樹創建決策點。

如果您有興趣了解有關機器學習的更多信息，請查看 IIIT-B 和 upGrad 的機器學習和人工智能 PG 文憑，該文憑專為工作專業人士設計，提供 450 多個小時的嚴格培訓、30 多個案例研究和作業、IIIT- B 校友身份、5 個以上實用的實踐頂點項目和頂級公司的工作協助。