決定木のジニ係数：メカニズム、例を使用した完全および不完全な分割

序章

デシジョンツリーは、教師あり学習で最も一般的に使用される実用的なアプローチの1つです。 回帰タスクと分類タスクの両方を解決するために使用でき、後者はより実用化されています。 これらのツリーでは、クラスラベルは葉で表され、ブランチはそれらのクラスラベルにつながる機能の接続詞を示します。 機械学習アルゴリズムで広く使用されています。 通常、機械学習アプローチには、多くのハイパーパラメータと最適化の制御が含まれます。

回帰ツリーは、予測された結果が実数である場合に使用され、分類ツリーは、データが属するクラスを予測するために使用されます。 これらの2つの用語は、まとめて分類および回帰ツリー（CART）と呼ばれます。

これらは、従属変数がそれぞれカテゴリ型か数値型かによって、回帰ツリーまたは分類ツリーを提供するノンパラメトリック決定木学習手法です。 このアルゴリズムは、ジニ係数のメソッドを展開してバイナリ分割を開始します。 GiniIndexとGiniImpurityはどちらも同じ意味で使用されます。

決定木は、機械学習の回帰モデルに影響を与えています。 ツリーを設計する際、開発者はノードの機能とその機能の可能な属性をエッジで設定します。

計算

ジニ係数またはジニ不純物は、各クラスの確率の2乗の合計を1から引くことによって計算されます。 これは主に大きなパーティションを優先し、実装は非常に簡単です。 簡単に言うと、ランダムに選択された特定の機能が誤って分類された確率を計算します。

ジニ係数は0から1の間で変化します。ここで、0は分類の純度を表し、1はさまざまなクラス間の要素のランダムな分布を表します。 ジニ係数0.5は、いくつかのクラスに要素が均等に分布していることを示しています。

数学的には、ジニ係数は次のように表されます。

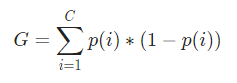
ジニ係数はカテゴリ変数に作用し、「成功」または「失敗」の観点から結果を提供するため、バイナリ分割のみを実行します。 それに対応する情報ゲインのように、計算集約的ではありません。 ジニ係数から、ジニゲインという名前の別のパラメーターの値が計算されます。このパラメーターの値は、決定木によって反復ごとに最大化され、完全なCARTを取得します。

簡単な例でジニ係数の計算を理解しましょう。 これには、赤と青の2つの変数を持つ合計10個のデータポイントがあります。 X軸とY軸には、各項の間に100のスペースを入れて番号が付けられています。 与えられた例から、ジニ係数とジニゲインを計算します。

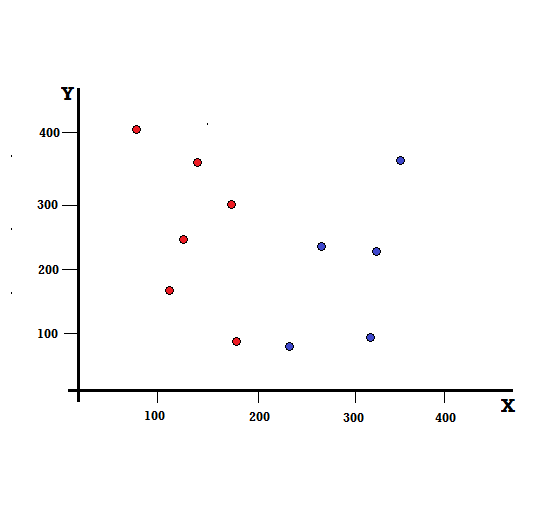
デシジョンツリーの場合、データセットを2つのブランチに分割する必要があります。 XY平面に5つの赤と5つの青がマークされた次のデータポイントについて考えてみます。 X = 200でバイナリ分割を行うとすると、次のように完全に分割されます。

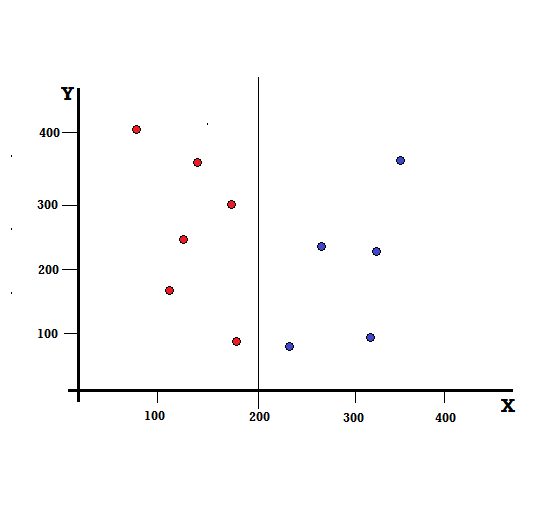
分割が正しく実行され、それぞれ5つの赤（左のブランチ）と5つの青（右のブランチ）を持つ2つのブランチが残っていることがわかります。

しかし、X = 250で分割すると、結果はどうなるでしょうか。

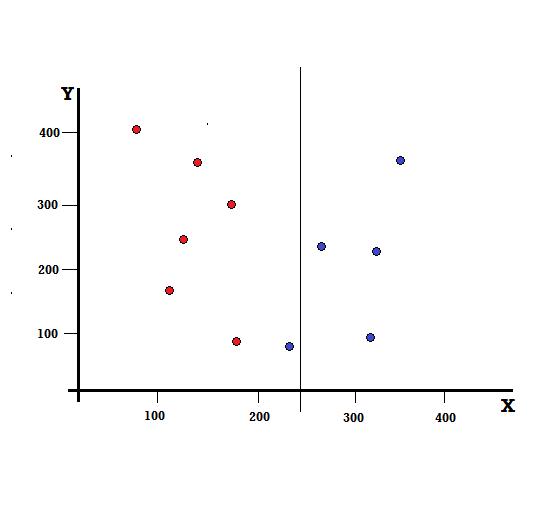
左の枝は5つの赤と1つの青で構成され、右の枝は4つの青で構成されています。 以下は不完全分割と呼ばれます。 デシジョンツリーモデルのトレーニングでは、分割の不完全さの量を定量化するために、ジニ係数を使用できます。

チェックアウト：二分木の種類

基本的なメカニズム

Gini Impurityを計算するために、最初にそれの基本的なメカニズムを理解しましょう。

• まず、データセットから任意のデータポイントをランダムに取得します
• 次に、指定されたデータセットのクラス分布に従ってランダムに分類します。 私たちのデータセットでは、各色のデータポイントが5つあるため、確率が赤の場合は5/10、青の場合は5/10の確率で選択されたデータポイントを指定します。

ここで、ジニ係数を計算するために、式は次のように与えられます。

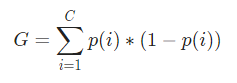
ここで、Cはクラスの総数であり、p（ i ）はクラスiでデータポイントを選択する確率です。

上記の例では、C = 2およびp（1）= p（2）= 0.5であるため、ジニ係数は次のように計算できます。

G = p（1） ∗ （1-p（1））+ p（2） ∗ （1-p（2））

= 0.5 ∗ （1−0.5）+ 0.5 ∗ （1−0.5）

= 0.5

ここで、0.5はデータポイントを不完全に分類する確率の合計であり、したがって正確に50％です。

ここで、以前に実行した完全分割と不完全分割の両方のGiniImpurityを計算してみましょう。

パーフェクトスプリット

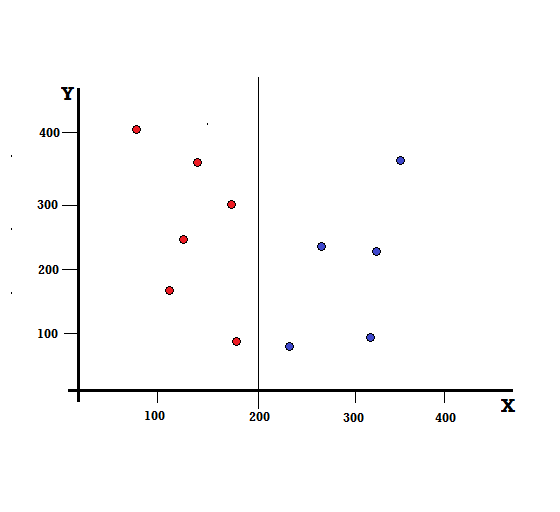
左の枝には赤しかなく、したがってそのジニ不純物は、

G（左）= 1 ∗ （1-1）+ 0 ∗ （1−0）= 0

右側のブランチにもブルースしかないため、そのGiniImpurityも次のように与えられます。

G（右）= 1 ∗ （1-1）+ 0 ∗ （1−0）= 0

簡単な計算から、完全分割の左分岐と右分岐の両方の確率が0であることがわかります。したがって、実際に完全です。 Gini不純物0は、データセットの中で可能な限り最低で最高の不純物です。

不完全な分割

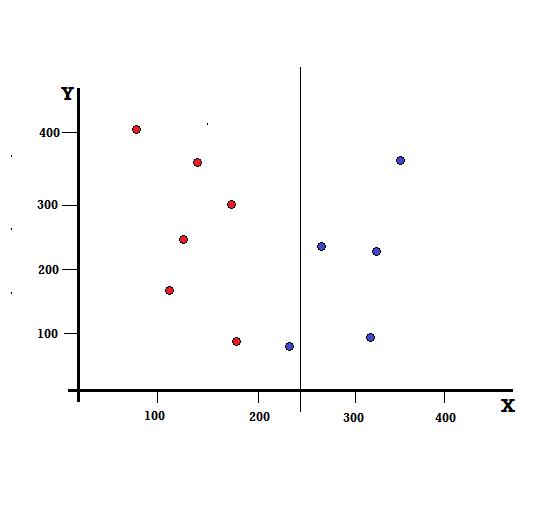
この場合、左側のブランチには5つの赤と1つの青があります。 そのジニ不純物は、によって与えることができます、

G（左）= 1/6 ∗ （1−1 / 6）+ 5/6 ∗ （1−5 / 6）= 0.278

右側のブランチにはすべてブルーが含まれているため、上記で計算すると、そのGini不純物は次の式で与えられます。

G（右）= 1 ∗ （1-1）+ 0 ∗ （1−0）= 0

不完全な分割のジニ不純物が得られたので、分割の品質または範囲を評価するために、各ブランチの不純物に、それが持つ要素の数で特定の重みを与えます。

（0.6 ∗ 0.278）+（0.4 ∗ 0）= 0.167

ジニ係数を計算したので、別のパラメーターであるジニゲインの値を計算し、そのアプリケーションをディシジョンツリーで分析します。 この分割で除去された不純物の量は、データセット全体のジニ係数（0.5）で上記の値を差し引くことによって計算されます。

0.5 – 0.167 = 0.333

計算されたこの値は「ジニゲイン」と呼ばれます。 簡単に言えば、より高いジニゲイン=より良い分割。

したがって、ディシジョンツリーアルゴリズムでは、各反復で上記の方法で計算されるジニゲインを最大化することによって最良の分割が得られます。

データセット内の各属性のジニゲインを計算した後、クラスsklearn.tree.DecisionTreeClassifierは、ルートノードとして最大のジニゲインを選択します。 Giniが0のブランチが検出されると、それはリーフノードになり、Giniが0を超える他のブランチはさらに分割する必要があります。 これらのノードは、すべてが分類されるまで再帰的に成長します。

機械学習での使用

機械学習の世界には、さまざまな目的のために設計されたさまざまなアルゴリズムがあります。 問題は、特定のデータセットに最適なアルゴリズムを特定することにあります。 デシジョンツリーアルゴリズムも説得力のある結果を示しているようです。 それを認識するためには、決定木が人間の主観的な力をいくらか模倣していると考えなければなりません。

したがって、より人間的な認知的質問の問題は、決定木により適している可能性があります。 決定木の根底にある概念は、そのツリーのような構造で簡単に理解できます。

また読む： AIのディシジョンツリー：はじめに、タイプ、作成

結論

ジニ係数の代わりに、クラスに関する最大の情報を提供する属性を決定するために使用される情報エントロピーがあります。 これは、不純物または不確実性の程度であるエントロピーの概念に基づいています。 これは、決定木のルートノードからリーフノードへのエントロピーのレベルを下げることを目的としています。

このように、ジニ係数はCARTアルゴリズムによって使用され、決定木を最適化し、分類木の決定点を作成します。

機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのPGディプロマをご覧ください。これは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディと課題、IIIT-を提供します。 B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との仕事の支援。