Indeks Giniego dla drzew decyzyjnych: mechanizm, doskonały i niedoskonały podział z przykładami

Wstęp

Drzewo decyzyjne jest jednym z najczęściej stosowanych, praktycznych podejść do nadzorowanego uczenia się. Może być używany do rozwiązywania zarówno zadań regresji, jak i klasyfikacji, przy czym te ostatnie są bardziej praktyczne. W tych drzewach etykiety klas są reprezentowane przez liście, a gałęzie oznaczają połączenia cech prowadzących do tych etykiet klas. Jest szeroko stosowany w algorytmach uczenia maszynowego. Zazwyczaj podejście do uczenia maszynowego obejmuje kontrolowanie wielu hiperparametrów i optymalizacji.

Drzewo regresji jest używane, gdy przewidywany wynik jest liczbą rzeczywistą, a drzewo klasyfikacyjne służy do przewidywania klasy, do której należą dane. Te dwa terminy są zbiorczo nazywane drzewami klasyfikacyjnymi i regresyjnymi (CART).

Są to nieparametryczne techniki uczenia drzew decyzyjnych, które zapewniają drzewa regresji lub klasyfikacyjne, w zależności od tego, czy zmienna zależna jest odpowiednio jakościowa czy liczbowa. Algorytm ten wykorzystuje metodę Gini Index do tworzenia podziałów binarnych. Zarówno Gini Index, jak i Gini Impurity są używane zamiennie.

Drzewa decyzyjne wpłynęły na modele regresji w uczeniu maszynowym. Projektując drzewo, programiści ustawiają cechy węzłów i możliwe atrybuty tej cechy za pomocą krawędzi.

Obliczenie

Indeks Giniego lub zanieczyszczenie Giniego oblicza się, odejmując sumę kwadratów prawdopodobieństw każdej klasy od jednego. Preferuje głównie większe przegrody i jest bardzo prosty w realizacji. Mówiąc prościej, oblicza prawdopodobieństwo wystąpienia pewnej losowo wybranej cechy, która została nieprawidłowo sklasyfikowana.

Indeks Giniego waha się od 0 do 1, gdzie 0 oznacza czystość klasyfikacji, a 1 oznacza losowy rozkład pierwiastków pomiędzy różnymi klasami. Indeks Giniego równy 0,5 pokazuje, że istnieje równy rozkład elementów w niektórych klasach.

Matematycznie Indeks Giniego jest reprezentowany przez

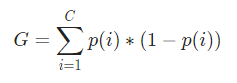
Indeks Giniego działa na zmiennych kategorycznych i podaje wyniki w kategoriach „sukcesu” lub „porażki”, a zatem wykonuje tylko podział binarny. Nie jest tak intensywny obliczeniowo jak jego odpowiednik – Information Gain. Z indeksu Gini obliczana jest wartość innego parametru o nazwie Gini Gain, którego wartość jest maksymalizowana w każdej iteracji przez drzewo decyzyjne, aby uzyskać idealny CART

Zrozummy obliczenie Indeksu Giniego na prostym przykładzie. W tym, mamy w sumie 10 punktów danych z dwiema zmiennymi, czerwonymi i niebieskimi. Osie X i Y są ponumerowane ze spacjami po 100 między każdym terminem. Z podanego przykładu obliczymy Indeks Giniego i Zysk Giniego.

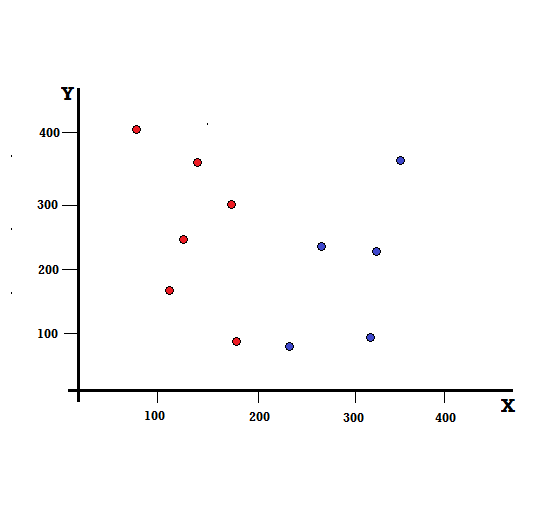
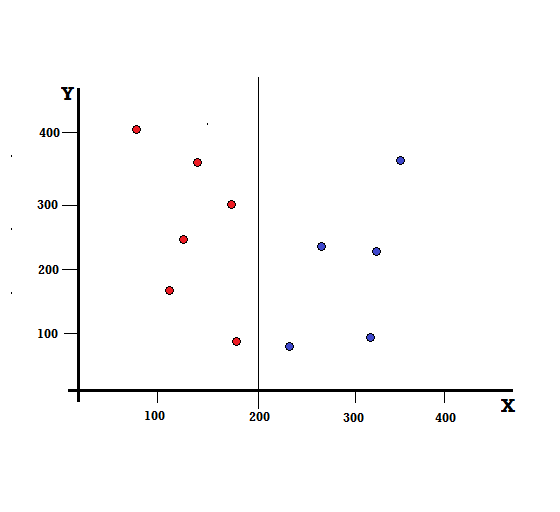
W przypadku drzewa decyzyjnego musimy podzielić zbiór danych na dwie gałęzie. Rozważ następujące punkty danych z 5 czerwonymi i 5 niebieskimi zaznaczonymi na płaszczyźnie XY. Załóżmy, że dokonujemy podziału binarnego przy X=200, wtedy otrzymamy idealny podział, jak pokazano poniżej.

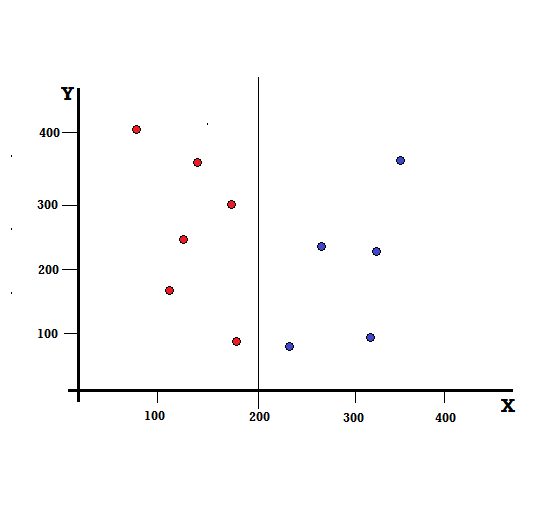
Widać, że podział jest prawidłowo wykonany i zostają nam dwie gałęzie, każda z 5 czerwonymi (lewa gałąź) i 5 niebieskimi (prawa gałąź).

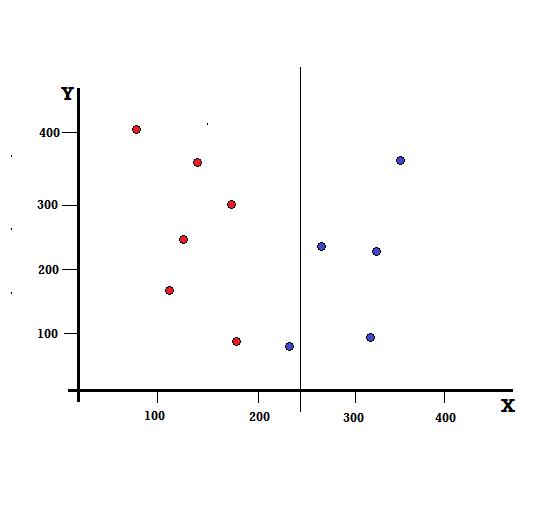
Ale jaki będzie wynik, jeśli dokonamy podziału przy X=250?

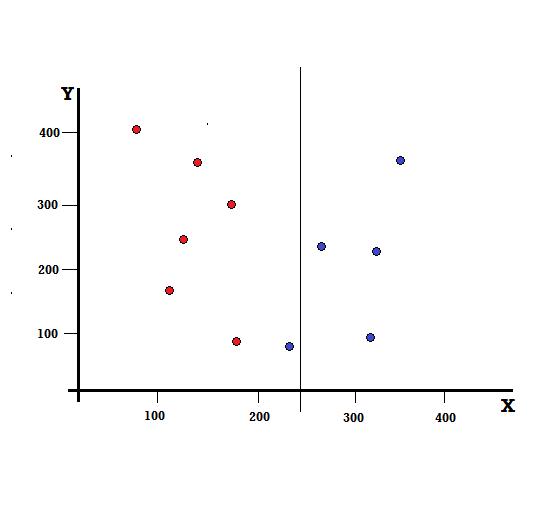
Pozostały nam dwie gałęzie, lewa gałąź składająca się z 5 czerwonych i 1 niebieskiego, a prawa gałąź składa się z 4 niebieskich. Poniższe jest określane jako niedoskonały podział. W trenowaniu modelu drzewa decyzyjnego, aby określić ilościowo ilość niedoskonałości podziału, możemy użyć indeksu Giniego.

Zamówienie: rodzaje drzewa binarnego

Mechanizm podstawowy

Aby obliczyć zanieczyszczenie Gini , najpierw zrozummy jego podstawowy mechanizm.

• Najpierw losowo wybierzemy dowolny punkt danych ze zbioru danych
• Następnie zaklasyfikujemy go losowo zgodnie z rozkładem klas w danym zbiorze danych. W naszym zestawie danych podamy wybrany punkt danych z prawdopodobieństwem 5/10 dla koloru czerwonego i 5/10 dla koloru niebieskiego, ponieważ istnieje pięć punktów danych każdego koloru, a zatem prawdopodobieństwo.

Teraz, aby obliczyć Indeks Giniego, wzór jest podany przez

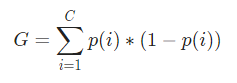
Gdzie C jest całkowitą liczbą klas, a p( i ) jest prawdopodobieństwem wybrania punktu danych z klasą i.

W powyższym przykładzie mamy C=2 i p(1) = p(2) = 0,5, stąd indeks Giniego można obliczyć jako,

G =p(1) ∗ (1−p(1)) + p(2) ∗ (1−p(2))

=0,5 (1−0,5) + 0,5 ∗ ( 1−0,5)

=0,5

Gdzie 0,5 to całkowite prawdopodobieństwo niedoskonałej klasyfikacji punktu danych, a zatem wynosi dokładnie 50%.

Teraz obliczmy zanieczyszczenie Giniego zarówno dla idealnego, jak i niedoskonałego podziału, który wykonaliśmy wcześniej,

Idealny podział

Lewa gałąź ma tylko czerwienie i stąd jej zanieczyszczenie Gini to:

G(lewo) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Prawa gałąź też ma tylko bluesa i stąd jej Gini Nieczystość jest również podana przez,

G(prawo) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Na podstawie szybkich obliczeń widzimy, że zarówno lewa, jak i prawa gałąź naszego idealnego podziału mają prawdopodobieństwa równe 0, a zatem są rzeczywiście doskonałe. Zanieczyszczenie Gini równe 0 jest najniższym i najlepszym możliwym zanieczyszczeniem dla dowolnego zestawu danych.

Niedoskonały podział

W tym przypadku lewa gałąź ma 5 czerwonych i 1 niebieski. Jego Nieczystość Gini może być dana przez,

G(lewo) =1/6 ∗ (1−1/6) + 5/6 ∗ (1−5/6) = 0,278

Prawa gałąź ma wszystkie bluesy, a zatem, jak obliczono powyżej, jej zanieczyszczenie Gini jest podane przez,

G(prawo) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Teraz, gdy mamy zanieczyszczenia Gini niedoskonałego podziału, aby ocenić jakość lub zakres podziału, przypiszemy konkretną wagę zanieczyszczenia każdej gałęzi wraz z liczbą elementów, które ma.

(0,6 ∗ 0,278) + (0,4 ∗ 0) = 0,167

Teraz, gdy obliczyliśmy Indeks Giniego, obliczymy wartość innego parametru, Gini Gain i przeanalizujemy jego zastosowanie w drzewach decyzyjnych. Ilość zanieczyszczeń usuniętych w tym podziale jest obliczana przez odjęcie powyższej wartości z indeksem Giniego dla całego zbioru danych (0,5)

0,5 – 0,167 = 0,333

Ta obliczona wartość nazywana jest „ Gini Gain ”. Mówiąc prościej, wyższy zysk Gini = lepszy podział .

Stąd w algorytmie Drzewa Decyzyjnego najlepszy podział uzyskuje się poprzez maksymalizację zysku Giniego, który jest obliczany w powyższy sposób przy każdej iteracji.

Po obliczeniu wzmocnienia Gini dla każdego atrybutu w zestawie danych, klasa sklearn.tree.DecisionTreeClassifier wybierze największy zysk Gini jako węzeł główny. Gdy zostanie napotkana gałąź z Gini równym 0, staje się ona węzłem liścia, a pozostałe gałęzie z Gini większym niż 0 wymagają dalszego podziału. Węzły te są rozwijane rekurencyjnie, aż wszystkie zostaną sklasyfikowane.

Użyj w uczeniu maszynowym

W świecie uczenia maszynowego istnieją różne algorytmy zaprojektowane do różnych celów. Problem polega na określeniu, który algorytm najlepiej pasuje do danego zestawu danych. Algorytm drzewa decyzyjnego również wydaje się przedstawiać przekonujące wyniki. Aby to rozpoznać, trzeba pomyśleć, że drzewa decyzyjne niejako naśladują ludzką subiektywną moc.

Tak więc problem z bardziej ludzkim kwestionowaniem poznawczym prawdopodobnie będzie bardziej pasował do drzew decyzyjnych. Podstawowa koncepcja drzew decyzyjnych może być łatwo zrozumiała ze względu na ich strukturę podobną do drzewa.

Przeczytaj także: Drzewo decyzyjne w AI: wprowadzenie, typy i tworzenie

Wniosek

Alternatywą dla Indeksu Giniego jest Entropia Informacji, która służy do określenia, który atrybut daje nam maksimum informacji o klasie. Opiera się na pojęciu entropii, która jest stopniem nieczystości lub niepewności. Ma na celu zmniejszenie poziomu entropii od węzłów korzenia do węzłów liści drzewa decyzyjnego.

W ten sposób Indeks Giniego jest wykorzystywany przez algorytmy CART do optymalizacji drzew decyzyjnych i tworzenia punktów decyzyjnych dla drzew klasyfikacyjnych.

Jeśli chcesz dowiedzieć się więcej o uczeniu maszynowym, sprawdź dyplom PG IIIT-B i upGrad w uczeniu maszynowym i sztucznej inteligencji, który jest przeznaczony dla pracujących profesjonalistów i oferuje ponad 450 godzin rygorystycznego szkolenia, ponad 30 studiów przypadków i zadań, IIIT- Status absolwenta B, ponad 5 praktycznych, praktycznych projektów zwieńczenia i pomoc w pracy z najlepszymi firmami.