Índice Gini para árvores de decisão: mecanismo, divisão perfeita e imperfeita com exemplos

Introdução

A Árvore de Decisão é uma das abordagens práticas mais comumente usadas para o aprendizado supervisionado. Ele pode ser usado para resolver tarefas de Regressão e Classificação, sendo a última mais colocada em aplicação prática. Nessas árvores, os rótulos de classe são representados pelas folhas e os ramos denotam as conjunções de recursos que levam a esses rótulos de classe. É amplamente utilizado em algoritmos de aprendizado de máquina. Normalmente, uma abordagem de aprendizado de máquina inclui o controle de muitos hiperparâmetros e otimizações.

A árvore de regressão é usada quando o resultado previsto é um número real e a árvore de classificação é usada para prever a classe à qual os dados pertencem. Esses dois termos são chamados coletivamente de Árvores de Classificação e Regressão (CART).

Essas são técnicas de aprendizado de árvore de decisão não paramétrica que fornecem árvores de regressão ou classificação, dependendo se a variável dependente é categórica ou numérica, respectivamente. Este algoritmo implementa o método do Índice de Gini para originar divisões binárias. Ambos Gini Index e Gini Impureza são usados ​​de forma intercambiável.

As árvores de decisão influenciaram os modelos de regressão no aprendizado de máquina. Ao projetar a árvore, os desenvolvedores definem os recursos dos nós e os possíveis atributos desse recurso com arestas.

Cálculo

O Índice de Gini ou Impureza de Gini é calculado subtraindo-se a soma das probabilidades ao quadrado de cada classe de um. Favorece principalmente as partições maiores e são muito simples de implementar. Em termos simples, ele calcula a probabilidade de um determinado recurso selecionado aleatoriamente que foi classificado incorretamente.

O Índice de Gini varia entre 0 e 1, onde 0 representa a pureza da classificação e 1 denota a distribuição aleatória dos elementos entre as várias classes. Um índice de Gini de 0,5 mostra que há uma distribuição igual de elementos em algumas classes.

Matematicamente, o Índice de Gini é representado por

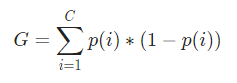
O Índice Gini funciona em variáveis ​​categóricas e fornece os resultados em termos de “sucesso” ou “fracasso” e, portanto, realiza apenas divisão binária. Não é computacionalmente intensivo como sua contraparte – Ganho de Informação. A partir do Índice de Gini, é calculado o valor de outro parâmetro denominado Gini Gain cujo valor é maximizado a cada iteração pela Árvore de Decisão para obter o CART perfeito

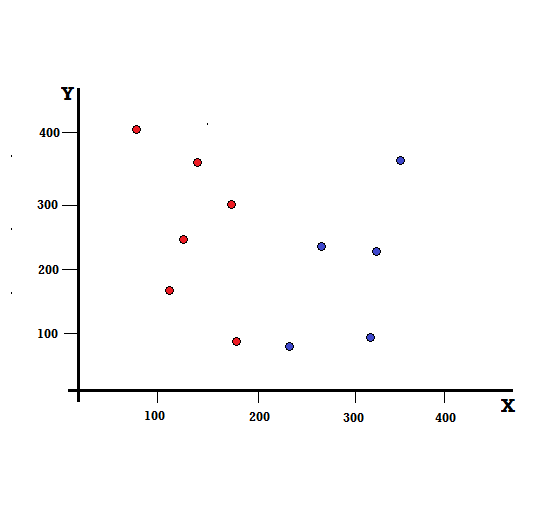
Vamos entender o cálculo do Índice de Gini com um exemplo simples. Neste, temos um total de 10 pontos de dados com duas variáveis, os vermelhos e os azuis. Os eixos X e Y são numerados com espaços de 100 entre cada termo. A partir do exemplo dado, calcularemos o Índice de Gini e o Ganho de Gini.

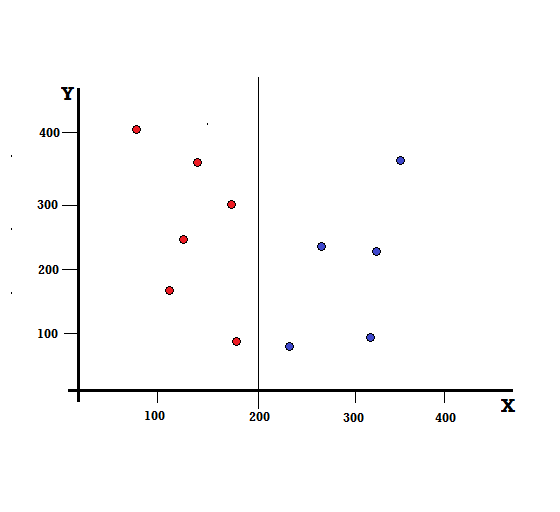
Para uma árvore de decisão, precisamos dividir o conjunto de dados em dois ramos. Considere os seguintes pontos de dados com 5 vermelhos e 5 azuis marcados no plano XY. Suponha que façamos uma divisão binária em X=200, então teremos uma divisão perfeita como mostrado abaixo.

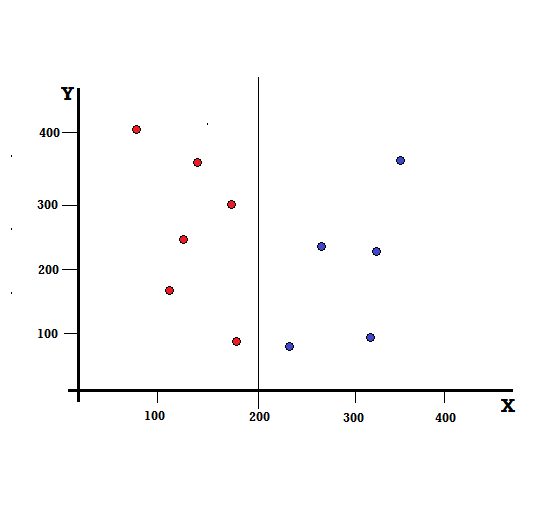
Vê-se que a divisão é realizada corretamente e ficamos com dois ramos cada um com 5 vermelhos (ramo esquerdo) e 5 azuis (ramo direito).

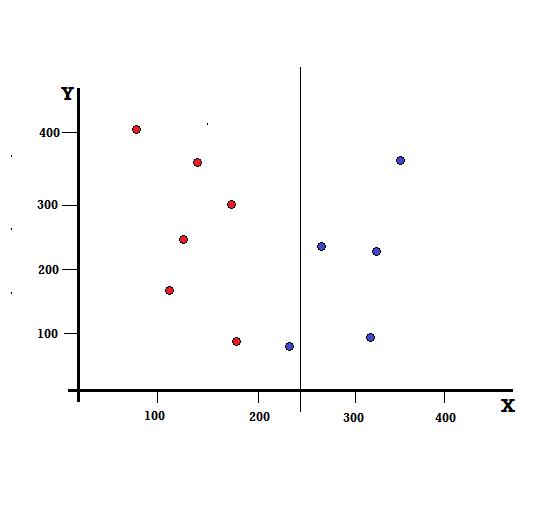
Mas qual será o resultado se fizermos a divisão em X=250?

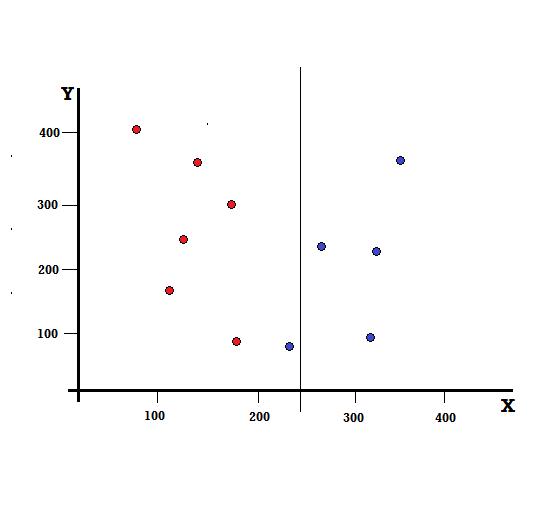
Ficamos com dois ramos, o ramo esquerdo composto por 5 vermelhos e 1 azul, enquanto o ramo direito consiste em 4 azuis. O seguinte é referido como uma divisão imperfeita. Ao treinar o modelo de Árvore de Decisão, para quantificar a quantidade de imperfeições da divisão, podemos utilizar o Índice de Gini.

Checkout: Tipos de Árvore Binária

Mecanismo Básico

Para calcular a Impureza Gini , vamos primeiro entender seu mecanismo básico.

• Primeiro, pegaremos aleatoriamente qualquer ponto de dados do conjunto de dados
• Então, vamos classificá-lo aleatoriamente de acordo com a distribuição de classes no conjunto de dados fornecido. Em nosso conjunto de dados, forneceremos um ponto de dados escolhido com uma probabilidade de 5/10 para vermelho e 5/10 para azul, pois há cinco pontos de dados de cada cor e, portanto, a probabilidade.

Agora, para calcular o Índice de Gini, a fórmula é dada por

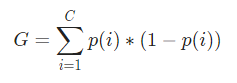
Onde, C é o número total de classes e p( i ) é a probabilidade de escolher o ponto de dados com a classe i.

No exemplo acima, temos C=2 e p(1) = p(2) = 0,5, portanto, o Índice de Gini pode ser calculado como,

G =p(1) ∗ (1−p(1)) + p(2) ∗ (1−p(2))

=0,5 ∗ (1−0,5) + 0,5 ∗ (1−0,5)

=0,5

Onde 0,5 é a probabilidade total de classificar um ponto de dados de forma imperfeita e, portanto, é exatamente 50%.

Agora, vamos calcular a impureza de Gini para a divisão perfeita e imperfeita que realizamos anteriormente,

Divisão Perfeita

O ramo esquerdo tem apenas vermelhos e, portanto, sua impureza Gini é,

G(esquerda) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

O ramo direito também tem apenas blues e, portanto, sua impureza Gini também é dada por,

G(direita) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

A partir do cálculo rápido, vemos que os ramos esquerdo e direito de nossa divisão perfeita têm probabilidades de 0 e, portanto, são de fato perfeitos. Uma Impureza Gini de 0 é a menor e a melhor impureza possível para qualquer conjunto de dados.

Divisão imperfeita

Neste caso, o ramo esquerdo tem 5 vermelhos e 1 azul. Sua impureza Gini pode ser dada por,

G(esquerda) =1/6 ∗ (1−1/6) + 5/6 ∗ (1−5/6) = 0,278

O ramo direito tem todos os azuis e, portanto, calculado acima de seu Gini Impureza é dado por,

G(direita) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Agora que temos as Impurezas Gini da cisão imperfeita, para avaliar a qualidade ou extensão da cisão, daremos um peso específico à impureza de cada ramo com o número de elementos que ela possui.

(0,6 ∗ 0,278) + (0,4 ∗ 0) = 0,167

Agora que calculamos o Índice de Gini, vamos calcular o valor de outro parâmetro, o Ganho de Gini e analisar sua aplicação em Árvores de Decisão. A quantidade de impureza removida com esta divisão é calculada deduzindo o valor acima com o Índice de Gini para todo o conjunto de dados (0,5)

0,5 – 0,167 = 0,333

Esse valor calculado é chamado de “ Ganho Gini ”. Em termos simples, maior ganho de Gini = melhor divisão .

Assim, em um algoritmo de árvore de decisão, a melhor divisão é obtida maximizando o ganho de Gini, que é calculado da maneira acima a cada iteração.

Após calcular o Gini Gain para cada atributo no conjunto de dados, a classe sklearn.tree.DecisionTreeClassifier escolherá o maior Gini Gain como o nó raiz. Quando uma ramificação com Gini de 0 é encontrada, ela se torna o nó folha e as outras ramificações com Gini maior que 0 precisam de mais divisão. Esses nós são crescidos recursivamente até que todos sejam classificados.

Uso em aprendizado de máquina

Existem vários algoritmos projetados para diferentes propósitos no mundo do aprendizado de máquina. O problema está em identificar qual algoritmo se adequa melhor a um determinado conjunto de dados. O algoritmo da árvore de decisão também parece mostrar resultados convincentes. Para reconhecê-lo, deve-se pensar que as árvores de decisão imitam um pouco o poder subjetivo humano.

Portanto, um problema com mais questionamento cognitivo humano provavelmente será mais adequado para árvores de decisão. O conceito subjacente de árvores de decisão pode ser facilmente entendido por sua estrutura em forma de árvore.

Leia também: Árvore de decisão em IA: introdução, tipos e criação

Conclusão

Uma alternativa ao Índice de Gini é a Entropia de Informação que é usada para determinar qual atributo nos dá o máximo de informação sobre uma classe. Baseia-se no conceito de entropia, que é o grau de impureza ou incerteza. Ele visa diminuir o nível de entropia dos nós raiz para os nós folha da árvore de decisão.

Desta forma, o Índice de Gini é utilizado pelos algoritmos CART para otimizar as árvores de decisão e criar pontos de decisão para as árvores de classificação.

Se você estiver interessado em aprender mais sobre aprendizado de máquina, confira o PG Diploma in Machine Learning & AI do IIIT-B e upGrad, projetado para profissionais que trabalham e oferece mais de 450 horas de treinamento rigoroso, mais de 30 estudos de caso e atribuições, IIIT- B Status de ex-aluno, mais de 5 projetos práticos práticos e assistência de trabalho com as principais empresas.