Индекс Джини для деревьев решений: механизм, совершенное и несовершенное разделение с примерами

Введение

Дерево решений — один из наиболее часто используемых практических подходов к обучению с учителем. Его можно использовать для решения как задач регрессии, так и задач классификации, причем последняя более применима на практике. В этих деревьях метки классов представлены листьями, а ветви обозначают соединения признаков, ведущие к этим меткам классов. Он широко используется в алгоритмах машинного обучения. Как правило, подход машинного обучения включает в себя управление многими гиперпараметрами и оптимизацию.

Дерево регрессии используется, когда прогнозируемый результат является действительным числом, а дерево классификации используется для прогнозирования класса, к которому принадлежат данные. Эти два термина вместе называются деревьями классификации и регрессии (CART).

Это непараметрические методы обучения дерева решений, которые обеспечивают деревья регрессии или классификации в зависимости от того, является ли зависимая переменная категориальной или числовой соответственно. Этот алгоритм использует метод индекса Джини для создания двоичных разделений. Индекс Джини и примесь Джини взаимозаменяемы.

Деревья решений повлияли на модели регрессии в машинном обучении. При проектировании дерева разработчики задают функции узлов и возможные атрибуты этой функции с ребрами.

Расчет

Индекс Джини или примесь Джини рассчитывается путем вычитания суммы квадратов вероятностей каждого класса из единицы. Он предпочитает в основном большие разделы и очень прост в реализации. Проще говоря, он вычисляет вероятность того, что определенная случайно выбранная функция будет неправильно классифицирована.

Индекс Джини варьируется от 0 до 1, где 0 представляет чистоту классификации, а 1 обозначает случайное распределение элементов между различными классами. Индекс Джини, равный 0,5, указывает на равное распределение элементов по некоторым классам.

Математически индекс Джини представлен

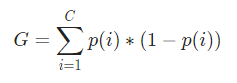
Индекс Джини работает с категориальными переменными и дает результаты в терминах «успех» или «неудача» и, следовательно, выполняет только бинарное разделение. Он не требует больших вычислительных ресурсов, как его аналог — получение информации. Из индекса Джини рассчитывается значение другого параметра, называемого Прирост Джини, значение которого максимизируется с каждой итерацией с помощью Дерева решений, чтобы получить идеальную КОРЗИНУ.

Давайте разберемся с расчетом индекса Джини на простом примере. Здесь у нас есть в общей сложности 10 точек данных с двумя переменными, красными и синими. Оси X и Y пронумерованы с пробелами 100 между каждым термином. Из данного примера мы рассчитаем индекс Джини и прирост Джини.

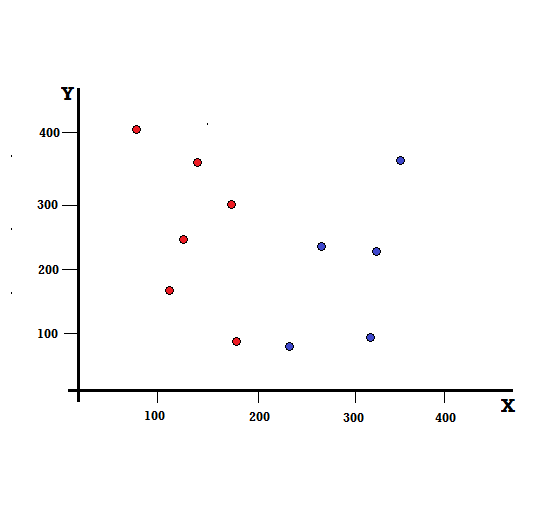
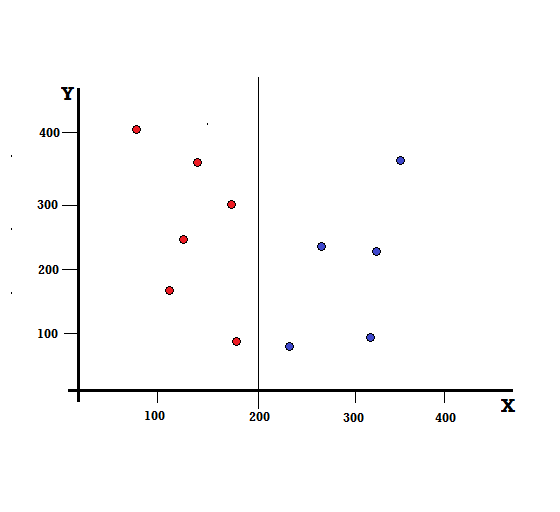
Для дерева решений нам нужно разделить набор данных на две ветви. Рассмотрим следующие точки данных с 5 красными и 5 синими точками, отмеченными на плоскости XY. Предположим, мы делаем бинарное разделение по X = 200, тогда у нас будет идеальное разделение, как показано ниже.

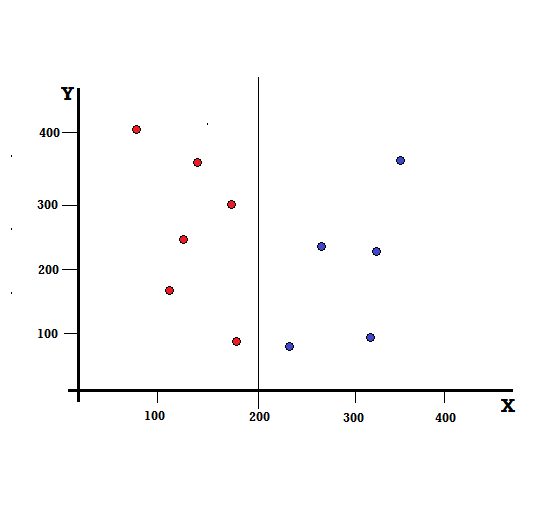
Видно, что разделение выполнено правильно и у нас осталось две ветви по 5 красных (левая ветвь) и 5 ​​синих (правая ветвь).

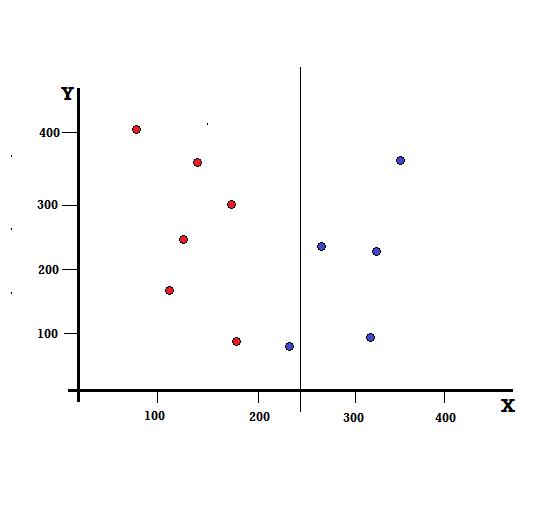
Но каков будет результат, если мы произведем расщепление по X=250?

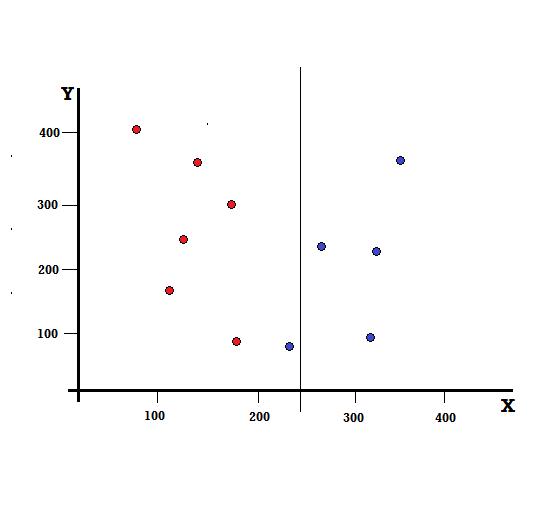
У нас осталось две ветви, левая ветвь состоит из 5 красных и 1 синей, а правая ветвь состоит из 4 синих. Следующее называется несовершенным разделением. При обучении модели дерева решений для количественной оценки степени несовершенства разделения мы можем использовать индекс Джини.

Оформить заказ: типы бинарного дерева

Основной механизм

Чтобы рассчитать примесь Джини , давайте сначала разберемся с ее основным механизмом.

• Во-первых, мы будем случайным образом выбирать любую точку данных из набора данных.
• Затем мы случайным образом классифицируем его в соответствии с распределением классов в данном наборе данных. В нашем наборе данных мы дадим точку данных, выбранную с вероятностью 5/10 для красного и 5/10 для синего, поскольку существует пять точек данных каждого цвета и, следовательно, вероятность.

Теперь, чтобы рассчитать индекс Джини, формула дается

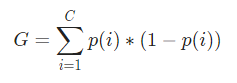
Где C — общее количество классов, а p( i ) — вероятность выбора точки данных с классом i.

В приведенном выше примере мы имеем C = 2 и p (1) = p (2) = 0,5. Следовательно, индекс Джини можно рассчитать как:

G =p(1) ∗ (1−p(1)) + p(2) ∗ (1−p(2))

=0,5 ∗ (1−0,5) + 0,5 ∗ (1−0,5)

=0,5

Где 0,5 — это общая вероятность несовершенной классификации точки данных и, следовательно, ровно 50%.

Теперь давайте рассчитаем примесь Джини как для идеального, так и для несовершенного разделения, которое мы выполнили ранее,

Идеальный сплит

Левая ветвь имеет только красные цвета, и, следовательно, ее примесь Джини:

G (слева) = 1 ∗ (1−1) + 0 ∗ (1−0) = 0

Правая ветвь также имеет только блюз, и, следовательно, ее примесь Джини также определяется как:

G (справа) = 1 ∗ (1−1) + 0 ∗ (1−0) = 0

Из быстрого вычисления мы видим, что как левая, так и правая ветви нашего идеального расщепления имеют вероятность 0 и, следовательно, действительно идеальны. Примесь Джини, равная 0, является самой низкой и наилучшей возможной примесью для любого набора данных.

Несовершенный раскол

В этом случае на левой ветке 5 красных и 1 синяя. Его примесь Джини может быть задана,

G (слева) = 1/6 * (1−1/6) + 5/6 * (1−5/6) = 0,278

Правая ветвь содержит все синие цвета, и, следовательно, как было рассчитано выше, ее примесь Джини определяется выражением

G (справа) = 1 ∗ (1−1) + 0 ∗ (1−0) = 0

Теперь, когда у нас есть примеси Джини несовершенного расщепления, чтобы оценить качество или степень расщепления, мы придадим определенный вес примеси каждой ветви с количеством элементов, которые она имеет.

(0,6 ∗ 0,278) + (0,4 ∗ 0) = 0,167

Теперь, когда мы рассчитали индекс Джини, мы вычислим значение другого параметра, усиления Джини, и проанализируем его применение в деревьях решений. Количество примесей, удаленных с помощью этого разделения, рассчитывается путем вычитания приведенного выше значения с индексом Джини для всего набора данных (0,5).

0,5 – 0,167 = 0,333

Это вычисленное значение называется « Gini Gain ». Проще говоря, более высокий коэффициент Джини = лучший сплит .

Следовательно, в алгоритме дерева решений наилучшее разделение получается путем максимизации коэффициента Джини, который рассчитывается вышеуказанным образом на каждой итерации.

После вычисления коэффициента Джини для каждого атрибута в наборе данных класс sklearn.tree.DecisionTreeClassifier выберет наибольший коэффициент Джини в качестве корневого узла. Когда встречается ветвь с Gini, равным 0, она становится конечным узлом, а другие ветви с Gini больше 0 нуждаются в дальнейшем разбиении. Эти узлы растут рекурсивно, пока все они не будут классифицированы.

Использование в машинном обучении

В мире машинного обучения существуют различные алгоритмы, предназначенные для разных целей. Проблема заключается в определении того, какой алгоритм лучше всего подходит для данного набора данных. Алгоритм дерева решений, похоже, тоже показывает убедительные результаты. Чтобы признать это, нужно думать, что деревья решений в чем-то имитируют человеческую субъективную силу.

Таким образом, проблема с более человеческим когнитивным опросом, вероятно, больше подходит для деревьев решений. Лежащая в основе концепция деревьев решений может быть легко понята благодаря их древовидной структуре.

Читайте также: Дерево решений в ИИ: введение, типы и создание

Заключение

Альтернативой индексу Джини является информационная энтропия, которая используется для определения того, какой атрибут дает нам максимальную информацию о классе. Он основан на понятии энтропии, которая представляет собой степень примеси или неопределенности. Он направлен на снижение уровня энтропии от корневых узлов к листовым узлам дерева решений.

Таким образом, индекс Джини используется алгоритмами CART для оптимизации деревьев решений и создания точек принятия решений для деревьев классификации.

Если вам интересно узнать больше о машинном обучении, ознакомьтесь с дипломом PG IIIT-B и upGrad в области машинного обучения и искусственного интеллекта, который предназначен для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 тематических исследований и заданий, IIIT- Статус B Alumni, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.