Karar Ağaçları için Gini İndeksi: Mekanizma, Örneklerle Mükemmel ve Kusurlu Bölünme

Tanıtım

Karar Ağacı, denetimli öğrenme için en yaygın kullanılan pratik yaklaşımlardan biridir. Hem Regresyon hem de Sınıflandırma görevlerini çözmek için kullanılabilir, ikincisi daha pratik uygulamaya konur. Bu ağaçlarda, sınıf etiketleri yapraklarla temsil edilir ve dallar, bu sınıf etiketlerine yol açan özelliklerin birleşimlerini gösterir. Makine öğrenimi algoritmalarında yaygın olarak kullanılmaktadır. Tipik olarak, bir makine öğrenimi yaklaşımı, birçok hiper parametrenin ve optimizasyonun kontrol edilmesini içerir.

Regresyon ağacı, tahmin edilen sonuç gerçek bir sayı olduğunda ve sınıflandırma ağacı, verilerin ait olduğu sınıfı tahmin etmek için kullanılır. Bu iki terim topluca Sınıflandırma ve Regresyon Ağaçları (CART) olarak adlandırılır.

Bunlar, bağımlı değişkenin sırasıyla kategorik mi yoksa sayısal mı olduğuna bağlı olarak, regresyon veya sınıflandırma ağaçları sağlayan parametrik olmayan karar ağacı öğrenme teknikleridir. Bu algoritma, ikili bölmeler oluşturmak için Gini İndeksi yöntemini kullanır. Hem Gini Index hem de Gini Impurity birbirinin yerine kullanılır.

Karar ağaçları, makine öğreniminde regresyon modellerini etkilemiştir. Ağacı tasarlarken, geliştiriciler düğümlerin özelliklerini ve bu özelliğin olası niteliklerini kenarlarla ayarlar.

Hesaplama

Gini İndeksi veya Gini Kirliliği, her bir sınıfın olasılıklarının karelerinin toplamının birden çıkarılmasıyla hesaplanır. Çoğunlukla daha büyük bölümleri tercih eder ve uygulanması çok basittir. Basit bir ifadeyle, yanlış sınıflandırılmış rastgele seçilmiş belirli bir özelliğin olasılığını hesaplar.

Gini İndeksi 0 ile 1 arasında değişir; burada 0, sınıflandırmanın saflığını temsil eder ve 1, çeşitli sınıflar arasında elementlerin rastgele dağılımını gösterir. 0,5'lik bir Gini İndeksi, bazı sınıflar arasında öğelerin eşit dağılımı olduğunu gösterir.

Matematiksel olarak, Gini Endeksi şu şekilde temsil edilir:

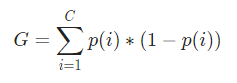
Gini Endeksi kategorik değişkenler üzerinde çalışır ve sonuçları "başarı" veya "başarısızlık" açısından verir ve bu nedenle yalnızca ikili bölme gerçekleştirir. Muadili olan Bilgi Kazancı kadar hesaplama açısından yoğun değildir. Gini İndeksinden, mükemmel CART'ı elde etmek için Karar Ağacı tarafından her yinelemede değeri en üst düzeye çıkarılan Gini Kazancı adlı başka bir parametrenin değeri hesaplanır.

Basit bir örnekle Gini Endeksi hesaplamasını anlayalım. Burada, kırmızılar ve maviler olmak üzere iki değişkenli toplam 10 veri noktamız var. X ve Y eksenleri, her terim arasında 100 boşluk bırakılarak numaralandırılmıştır. Verilen örnekten Gini İndeksi ve Gini Kazancı'nı hesaplayacağız.

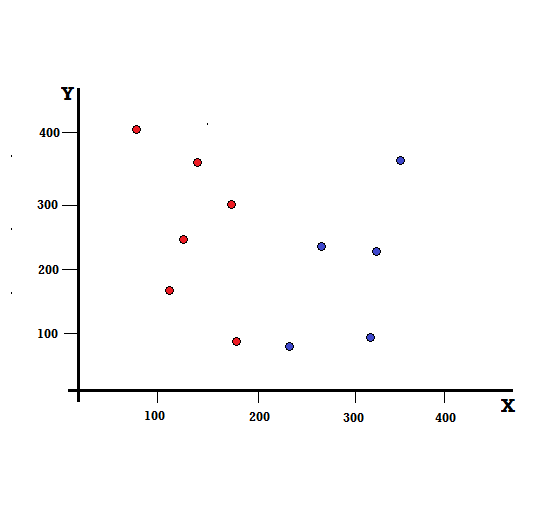
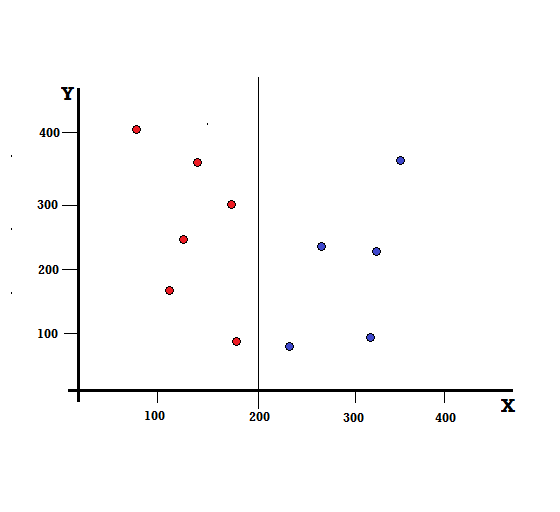
Bir karar ağacı için veri setini iki dala ayırmamız gerekir. XY düzleminde 5 Kırmızı ve 5 Mavi ile işaretlenmiş aşağıdaki veri noktalarını göz önünde bulundurun. X=200'de bir ikili bölme yaptığımızı varsayalım, o zaman aşağıda gösterildiği gibi mükemmel bir bölünme elde edeceğiz.

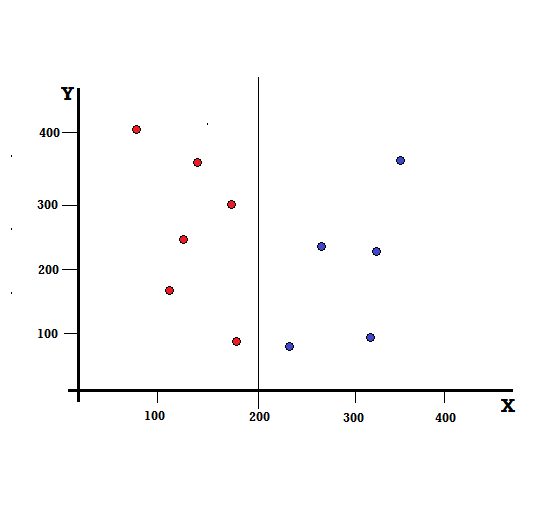
Bölmenin doğru yapıldığı görülüyor ve her biri 5 kırmızı (sol dal) ve 5 mavi (sağ dal) olmak üzere iki dal bırakıyoruz.

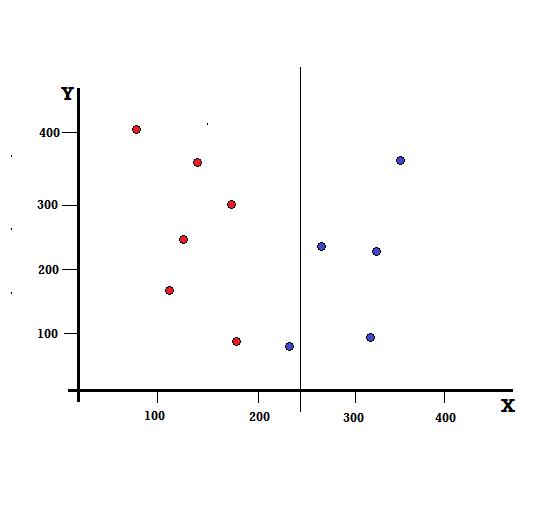
Ama bölmeyi X=250'de yaparsak sonuç ne olur?

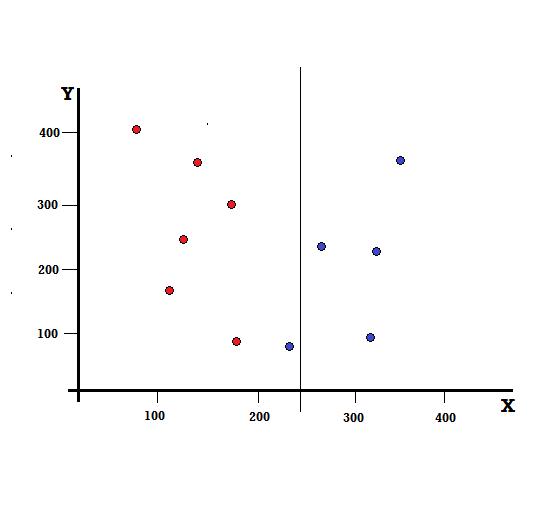
İki dalımız kaldı, sol dal 5 kırmızı ve 1 maviden, sağ dal ise 4 maviden oluşuyor. Aşağıdaki, kusurlu bir bölünme olarak adlandırılır. Karar Ağacı modelini eğitirken, bölünmenin kusurluluğunu ölçmek için Gini İndeksini kullanabiliriz.

Ödeme: İkili Ağaç Türleri

Temel Mekanizma

Gini Kirliliğini hesaplamak için önce temel mekanizmasını anlayalım.

• İlk olarak, veri kümesinden herhangi bir veri noktasını rastgele seçeceğiz.
• Ardından, verilen veri kümesindeki sınıf dağılımına göre rastgele sınıflandıracağız. Veri setimizde, her rengin beş veri noktası ve dolayısıyla olasılık olduğu için kırmızı için 5/10 ve mavi için 5/10 olasılıkla seçilen bir veri noktası vereceğiz.

Şimdi, Gini Endeksini hesaplamak için formül şu şekilde verilmektedir:

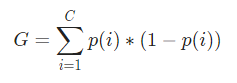
Burada, C, sınıfların toplam sayısıdır ve p( i ), i sınıfı ile veri noktasını seçme olasılığıdır .

Yukarıdaki örnekte, C=2 ve p(1) = p(2) = 0.5'e sahibiz, Dolayısıyla Gini İndeksi şu şekilde hesaplanabilir:

G =p(1) ∗ (1−p(1)) + p(2) ∗ (1−p(2))

=0.5 ∗ (1−0.5) + 0.5 ∗ (1−0.5)

=0.5

0,5, bir veri noktasını kusurlu olarak sınıflandırmanın toplam olasılığıdır ve dolayısıyla tam olarak %50'dir.

Şimdi, daha önce gerçekleştirdiğimiz hem mükemmel hem de kusurlu bölme için Gini Kirliliğini hesaplayalım,

Mükemmel Bölme

Sol dalda yalnızca kırmızılar vardır ve bu nedenle Gini Kirliliği,

G(sol) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Sağ dalda da sadece blues vardır ve bu nedenle Gini Kirliliği de şu şekilde verilir:

G(sağ) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Hızlı hesaplamadan, mükemmel bölünmemizin hem sol hem de sağ dallarının 0 olasılıklarına sahip olduğunu ve dolayısıyla gerçekten mükemmel olduğunu görüyoruz. 0'lık bir Gini Kirliliği, herhangi bir veri seti için mümkün olan en düşük ve en iyi kirliliktir.

kusurlu bölme

Bu durumda sol dalda 5 kırmızı ve 1 mavi vardır. Gini Kirliliği şu şekilde verilebilir,

G(sol) =1/6 ∗ (1−1/6) + 5/6 ∗ (1−5/6) = 0,278

Sağ dal tüm mavilere sahiptir ve bu nedenle yukarıda hesaplandığı gibi Gini Kirliliği şu şekilde verilir:

G(sağ) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Artık kusurlu bölünmenin Gini Safsızlıklarına sahip olduğumuza göre, bölünmenin kalitesini veya kapsamını değerlendirmek için, sahip olduğu element sayısı ile her dalın safsızlığına belirli bir ağırlık vereceğiz.

(0,6 ∗ 0,278) + (0,4 ∗ 0) = 0,167

Artık Gini İndeksini hesapladığımıza göre, başka bir parametre olan Gini Kazancının değerini hesaplayacağız ve Karar Ağaçlarındaki uygulamasını analiz edeceğiz. Bu bölme ile kaldırılan safsızlık miktarı, tüm veri kümesi için Gini İndeksi ile yukarıdaki değerin çıkarılmasıyla hesaplanır (0.5)

0,5 – 0,167 = 0,333

Hesaplanan bu değere “ Gini Kazanımı ” adı verilir. Basit bir ifadeyle, Daha Yüksek Gini Kazancı = Daha İyi Bölünme .

Bu nedenle, bir Karar Ağacı algoritmasında, her yinelemede yukarıdaki şekilde hesaplanan Gini Kazancının maksimize edilmesiyle en iyi bölme elde edilir.

Veri kümesindeki her bir öznitelik için Gini Kazancı hesaplandıktan sonra, sklearn.tree.DecisionTreeClassifier sınıfı, Kök Düğüm olarak en büyük Gini Kazancı'nı seçecektir. Gini'si 0 olan bir dalla karşılaşıldığında, yaprak düğüm olur ve Gini'si 0'dan büyük olan diğer dalların daha fazla bölünmesi gerekir. Bu düğümler, hepsi sınıflandırılana kadar özyinelemeli olarak büyütülür.

Makine Öğreniminde Kullanım

Makine öğrenimi dünyasında farklı amaçlar için tasarlanmış çeşitli algoritmalar bulunmaktadır. Sorun, belirli bir veri kümesine en uygun algoritmanın belirlenmesinde yatmaktadır. Karar ağacı algoritması da ikna edici sonuçlar veriyor gibi görünüyor. Bunu tanımak için, karar ağaçlarının bir şekilde insanın öznel gücünü taklit ettiğini düşünmek gerekir.

Bu nedenle, daha fazla insan bilişsel sorgulaması olan bir problemin karar ağaçları için daha uygun olması muhtemeldir. Karar ağaçlarının altında yatan kavram, ağaç benzeri yapısı nedeniyle kolayca anlaşılabilir.

Ayrıca Okuyun: Yapay Zekada Karar Ağacı: Giriş, Türler ve Oluşturma

Çözüm

Gini İndeksine bir alternatif, hangi niteliğin bize bir sınıf hakkında maksimum bilgi verdiğini belirlemek için kullanılan Bilgi Entropisi'dir. Safsızlık veya belirsizlik derecesi olan entropi kavramına dayanır. Karar ağacının kök düğümlerinden yaprak düğümlerine kadar entropi düzeyini düşürmeyi amaçlar.

Bu şekilde, Gini İndeksi, CART algoritmaları tarafından karar ağaçlarını optimize etmek ve sınıflandırma ağaçları için karar noktaları oluşturmak için kullanılır.

Makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, çalışan profesyoneller için tasarlanmış ve 450+ saat zorlu eğitim, 30'dan fazla vaka çalışması ve ödev, IIIT- sunan IIIT-B & upGrad'ın Makine Öğrenimi ve Yapay Zeka PG Diplomasına göz atın. B Mezun statüsü, 5+ pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.