Indice de Gini pour les arbres de décision : mécanisme, répartition parfaite et imparfaite avec exemples

introduction

L'arbre de décision est l'une des approches pratiques les plus couramment utilisées pour l'apprentissage supervisé. Il peut être utilisé pour résoudre à la fois des tâches de régression et de classification, ces dernières étant davantage mises en pratique. Dans ces arbres, les étiquettes de classe sont représentées par les feuilles et les branches dénotent les conjonctions d'entités menant à ces étiquettes de classe. Il est largement utilisé dans les algorithmes d'apprentissage automatique. En règle générale, une approche d'apprentissage automatique comprend le contrôle de nombreux hyperparamètres et optimisations.

L'arbre de régression est utilisé lorsque le résultat prédit est un nombre réel et l'arbre de classification est utilisé pour prédire la classe à laquelle appartiennent les données. Ces deux termes sont collectivement appelés arbres de classification et de régression (CART).

Il s'agit de techniques d'apprentissage d'arbres de décision non paramétriques qui fournissent des arbres de régression ou de classification, selon que la variable dépendante est respectivement catégorielle ou numérique. Cet algorithme déploie la méthode de l'indice de Gini pour créer des divisions binaires. L'indice de Gini et l'impureté de Gini sont utilisés de manière interchangeable.

Les arbres de décision ont influencé les modèles de régression dans l'apprentissage automatique. Lors de la conception de l'arborescence, les développeurs définissent les fonctionnalités des nœuds et les attributs possibles de cette fonctionnalité avec des arêtes.

Calcul

L'indice de Gini ou l'impureté de Gini est calculé en soustrayant la somme des probabilités au carré de chaque classe de un. Il privilégie surtout les grandes partitions et est très simple à mettre en œuvre. En termes simples, il calcule la probabilité qu'une certaine caractéristique sélectionnée au hasard ait été classée de manière incorrecte.

L'indice de Gini varie entre 0 et 1, où 0 représente la pureté de la classification et 1 dénote une distribution aléatoire des éléments parmi les différentes classes. Un indice de Gini de 0,5 montre qu'il y a une répartition égale des éléments dans certaines classes.

Mathématiquement, l'indice de Gini est représenté par

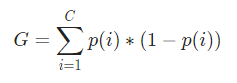
L'indice de Gini fonctionne sur des variables catégorielles et donne les résultats en termes de "succès" ou "échec" et n'effectue donc qu'une division binaire. Il n'est pas intensif en calcul comme son homologue - Information Gain. À partir de l'indice de Gini, la valeur d'un autre paramètre nommé Gini Gain est calculée dont la valeur est maximisée à chaque itération par l'arbre de décision pour obtenir le CART parfait

Comprenons le calcul de l'indice de Gini avec un exemple simple. En cela, nous avons un total de 10 points de données avec deux variables, les rouges et les bleus. Les axes X et Y sont numérotés avec des espaces de 100 entre chaque terme. À partir de l'exemple donné, nous allons calculer l'indice de Gini et le gain de Gini.

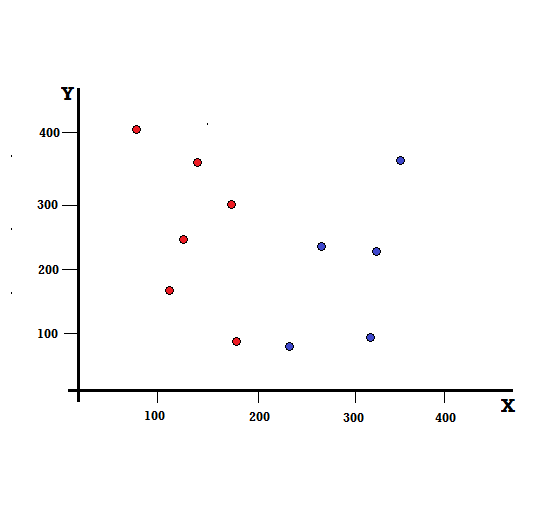
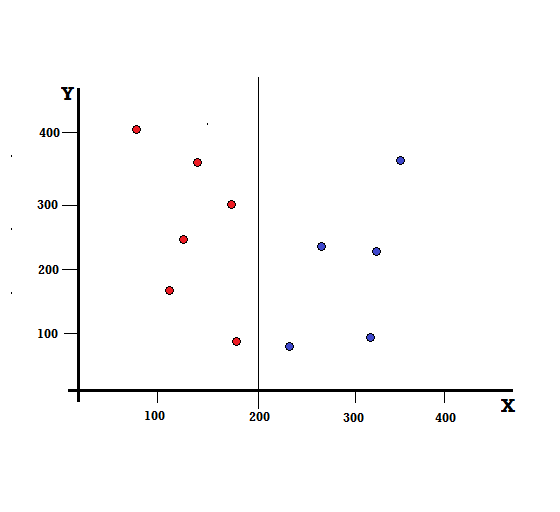
Pour un arbre de décision, nous devons diviser l'ensemble de données en deux branches. Considérez les points de données suivants avec 5 rouges et 5 bleus marqués sur le plan XY. Supposons que nous fassions une division binaire à X = 200, nous aurons alors une division parfaite comme indiqué ci-dessous.

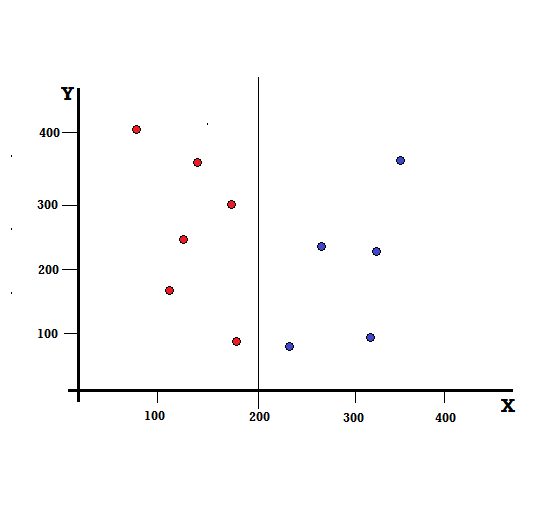
On voit que le split est correctement effectué et on se retrouve avec deux branches avec chacune 5 rouges (branche gauche) et 5 bleus (branche droite).

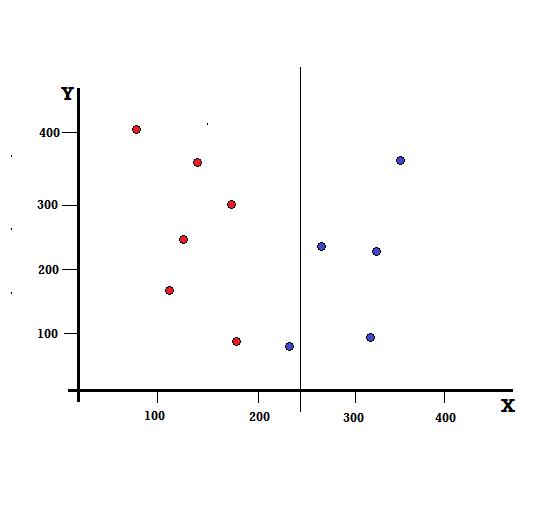
Mais quel sera le résultat si nous faisons le split à X=250 ?

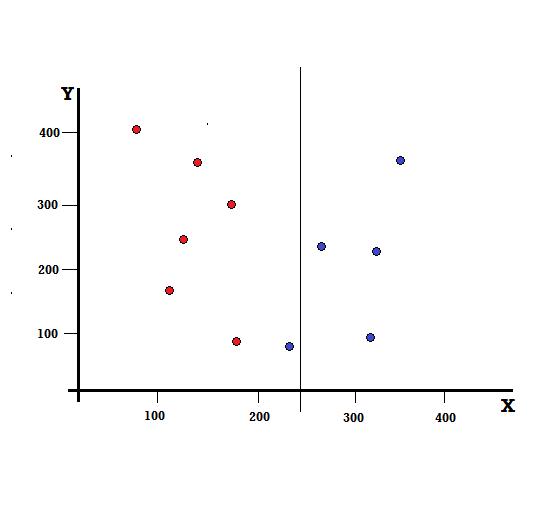
Il nous reste deux branches, la branche gauche composée de 5 rouges et 1 bleu, tandis que la branche droite est composée de 4 bleus. Ce qui suit est appelé une division imparfaite. Lors de la formation du modèle d'arbre de décision, pour quantifier le degré d'imperfection de la scission, nous pouvons utiliser l'indice de Gini.

Paiement : Types d'arbre binaire

Mécanisme de base

Pour calculer l' impureté de Gini , comprenons d'abord son mécanisme de base.

• Tout d'abord, nous allons choisir au hasard n'importe quel point de données de l'ensemble de données
• Ensuite, nous le classerons de manière aléatoire en fonction de la distribution des classes dans l'ensemble de données donné. Dans notre ensemble de données, nous donnerons un point de données choisi avec une probabilité de 5/10 pour le rouge et de 5/10 pour le bleu car il y a cinq points de données de chaque couleur et donc la probabilité.

Maintenant, pour calculer l'indice de Gini, la formule est donnée par

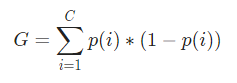
Où, C est le nombre total de classes et p( i ) est la probabilité de choisir le point de données avec la classe i.

Dans l'exemple ci-dessus, nous avons C=2 et p(1) = p(2) = 0,5. Par conséquent, l'indice de Gini peut être calculé comme suit :

G =p(1) ∗ (1−p(1)) + p(2) ∗ (1−p(2))

=0,5 ∗ (1−0,5) + 0,5 ∗ (1−0,5)

=0,5

Où 0,5 est la probabilité totale de classer un point de données de manière imparfaite et est donc exactement de 50 %.

Maintenant, calculons l'impureté de Gini pour la division parfaite et imparfaite que nous avons effectuée plus tôt,

Partage parfait

La branche de gauche n'a que des rouges et donc son impureté de Gini est,

G(gauche) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

La branche droite n'a également que du blues et donc son impureté de Gini est également donnée par,

G(droite) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

D'après le calcul rapide, nous voyons que les branches gauche et droite de notre division parfaite ont des probabilités de 0 et sont donc en effet parfaites. Une impureté Gini de 0 est la plus faible et la meilleure impureté possible pour tout ensemble de données.

Fractionnement imparfait

Dans ce cas, la branche de gauche a 5 rouges et 1 bleue. Son impureté de Gini peut être donnée par,

G(gauche) =1/6 ∗ (1−1/6) + 5/6 ∗ (1−5/6) = 0,278

La branche droite a tous les bleus et donc, comme calculé ci-dessus, son impureté Gini est donnée par,

G(droite) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Maintenant que nous avons les impuretés de Gini de la scission imparfaite, afin d'évaluer la qualité ou l'étendue de la scission, nous allons donner un poids spécifique à l'impureté de chaque branche avec le nombre d'éléments dont elle dispose.

(0,6 ∗ 0,278) + (0,4 ∗ 0) = 0,167

Maintenant que nous avons calculé l'indice de Gini, nous allons calculer la valeur d'un autre paramètre, Gini Gain et analyser son application dans les arbres de décision. La quantité d'impuretés éliminées avec cette division est calculée en déduisant la valeur ci-dessus avec l'indice de Gini pour l'ensemble de données (0,5)

0,5 – 0,167 = 0,333

Cette valeur calculée est appelée « Gini Gain ». En termes simples, gain de Gini supérieur = meilleure répartition .

Par conséquent, dans un algorithme d'arbre de décision, la meilleure répartition est obtenue en maximisant le gain de Gini, qui est calculé de la manière ci-dessus à chaque itération.

Après avoir calculé le gain de Gini pour chaque attribut de l'ensemble de données, la classe sklearn.tree.DecisionTreeClassifier choisira le plus grand gain de Gini comme nœud racine. Lorsqu'une branche avec Gini de 0 est rencontrée, elle devient le nœud feuille et les autres branches avec Gini supérieur à 0 nécessitent un fractionnement supplémentaire. Ces nœuds sont développés de manière récursive jusqu'à ce qu'ils soient tous classés.

Utilisation dans l'apprentissage automatique

Il existe différents algorithmes conçus à des fins différentes dans le monde de l'apprentissage automatique. Le problème réside dans l'identification de l'algorithme le mieux adapté à un ensemble de données donné. L'algorithme de l'arbre de décision semble également montrer des résultats convaincants. Pour le reconnaître, il faut penser que les arbres de décision imitent quelque peu le pouvoir subjectif humain.

Ainsi, un problème avec un questionnement cognitif plus humain est susceptible d'être plus adapté aux arbres de décision. Le concept sous-jacent des arbres de décision peut être facilement compréhensible pour sa structure arborescente.

Lisez aussi : Arbre de décision en IA : introduction, types et création

Conclusion

Une alternative à l'indice de Gini est l'entropie d'information qui permet de déterminer quel attribut nous donne le maximum d'informations sur une classe. Il est basé sur le concept d'entropie, qui est le degré d'impureté ou d'incertitude. Il vise à diminuer le niveau d'entropie des nœuds racines aux nœuds feuilles de l'arbre de décision.

De cette manière, l'indice de Gini est utilisé par les algorithmes CART pour optimiser les arbres de décision et créer des points de décision pour les arbres de classification.

Si vous souhaitez en savoir plus sur l'apprentissage automatique, consultez le diplôme PG en apprentissage automatique et IA de IIIT-B & upGrad, conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, IIIT- Statut B Alumni, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.