Indicele Gini pentru arbori de decizie: mecanism, împărțire perfectă și imperfectă cu exemple

Introducere

Arborele decizional este una dintre cele mai frecvent utilizate abordări practice pentru învățarea supravegheată. Poate fi folosit pentru a rezolva atât sarcini de regresie, cât și de clasificare, acestea din urmă fiind puse mai mult în aplicare practică. În acești arbori, etichetele de clasă sunt reprezentate de frunze, iar ramurile denotă conjuncțiile caracteristicilor care conduc la acele etichete de clasă. Este utilizat pe scară largă în algoritmii de învățare automată. De obicei, o abordare de învățare automată include controlul multor hiperparametri și optimizări.

Arborele de regresie este utilizat atunci când rezultatul prezis este un număr real, iar arborele de clasificare este utilizat pentru a prezice clasa căreia îi aparțin datele. Acești doi termeni sunt numiți colectiv ca arbori de clasificare și regresie (CART).

Acestea sunt tehnici neparametrice de învățare a arborelui de decizie care oferă arbori de regresie sau clasificare, bazându-se pe faptul că variabila dependentă este categorială sau, respectiv, numerică. Acest algoritm implementează metoda indicelui Gini pentru a genera împărțiri binare. Atât Gini Index, cât și Gini Impurity sunt folosite interschimbabil.

Arborele de decizie au influențat modelele de regresie în învățarea automată. În timpul proiectării arborelui, dezvoltatorii setează caracteristicile nodurilor și atributele posibile ale acelei caracteristici cu margini.

Calcul

Indicele Gini sau Impuritatea Gini se calculează scăzând din unu suma probabilităților pătrate ale fiecărei clase. Favorizează mai ales partițiile mai mari și sunt foarte simplu de implementat. În termeni simpli, calculează probabilitatea unei anumite caracteristici alese aleatoriu care a fost clasificată incorect.

Indicele Gini variază între 0 și 1, unde 0 reprezintă puritatea clasificării și 1 denotă distribuția aleatorie a elementelor între diferitele clase. Un indice Gini de 0,5 arată că există o distribuție egală a elementelor în unele clase.

Matematic, Indicele Gini este reprezentat de

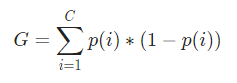
Indexul Gini lucrează pe variabile categorice și oferă rezultatele în termeni de „succes” sau „eșec” și, prin urmare, efectuează doar împărțirea binară. Nu este intensiv din punct de vedere al calculului ca omologul său - Câștig de informații. Din indicele Gini, se calculează valoarea unui alt parametru numit Câștig Gini a cărui valoare este maximizată cu fiecare iterație de Arborele de decizie pentru a obține CART-ul perfect.

Să înțelegem calculul indicelui Gini cu un exemplu simplu. În aceasta, avem un total de 10 puncte de date cu două variabile, roșul și albastrul. Axele X și Y sunt numerotate cu spații de 100 între fiecare termen. Din exemplul dat, vom calcula Indicele Gini și Câștigul Gini.

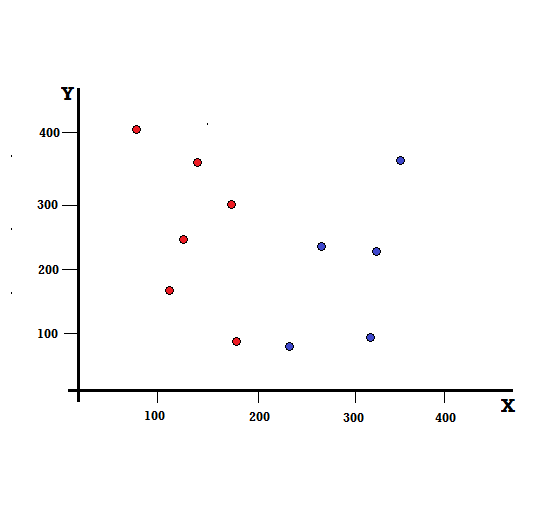
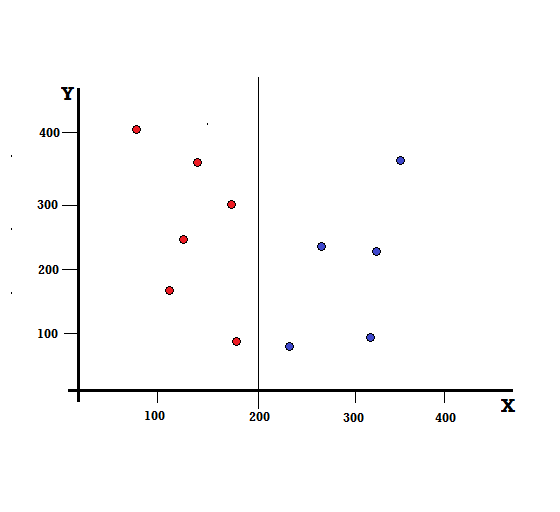
Pentru un arbore de decizie, trebuie să împărțim setul de date în două ramuri. Luați în considerare următoarele puncte de date cu 5 roșii și 5 albaștri marcate pe planul XY. Să presupunem că facem o împărțire binară la X=200, atunci vom avea o împărțire perfectă așa cum se arată mai jos.

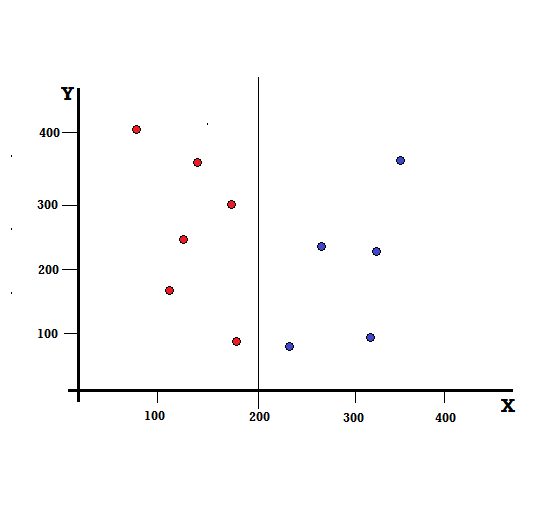
Se vede ca despicarea este corect efectuata si ne raman cate doua ramuri cu cate 5 rosii (ramura stanga) si 5 albastre (ramura dreapta).

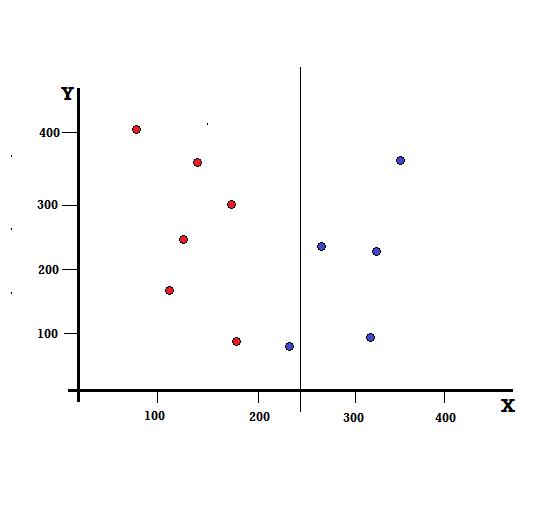
Dar care va fi rezultatul dacă facem împărțirea la X=250?

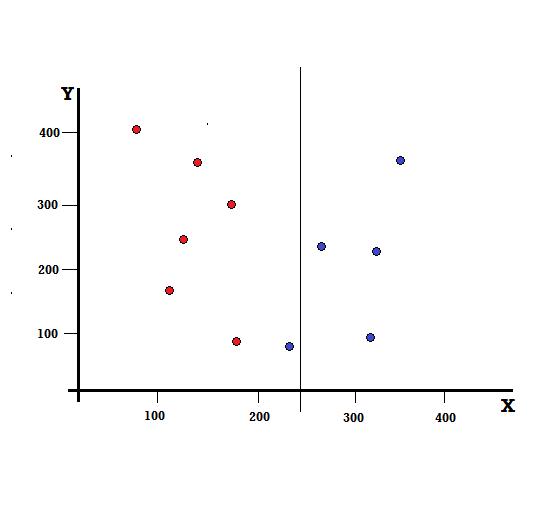
Ne-au rămas două ramuri, ramura stângă formată din 5 roșii și 1 albastru, în timp ce ramura dreaptă este formată din 4 albaștri. Următorul este denumit o împărțire imperfectă. În antrenarea modelului Decision Tree, pentru a cuantifica cantitatea de imperfecțiune a divizării, putem folosi indicele Gini.

Checkout: Tipuri de arbore binar

Mecanism de bază

Pentru a calcula Impuritatea Gini , să înțelegem mai întâi mecanismul de bază al acestuia.

• În primul rând, vom ridica aleatoriu orice punct de date din setul de date
• Apoi, îl vom clasifica aleatoriu în funcție de distribuția clasei din setul de date dat. În setul nostru de date, vom da un punct de date ales cu o probabilitate de 5/10 pentru roșu și 5/10 pentru albastru, deoarece există cinci puncte de date pentru fiecare culoare și, prin urmare, probabilitatea.

Acum, pentru a calcula Indicele Gini, formula este dată de

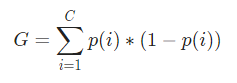
Unde, C este numărul total de clase și p( i ) este probabilitatea de a alege punctul de date cu clasa i.

În exemplul de mai sus, avem C=2 și p(1) = p(2) = 0,5, prin urmare indicele Gini poate fi calculat ca,

G =p(1) ∗ (1−p(1)) + p(2) ∗ (1−p(2))

=0,5 ∗ (1−0,5) + 0,5 ∗ (1−0,5)

=0,5

Unde 0,5 este probabilitatea totală de a clasifica imperfect un punct de date și, prin urmare, este exact 50%.

Acum, să calculăm Impuritatea Gini atât pentru împărțirea perfectă, cât și pentru cea imperfectă pe care am realizat-o mai devreme,

Split perfect

Ramura stângă are doar roșii și, prin urmare, impuritatea sa Gini este,

G(stânga) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

De asemenea, ramura dreaptă are doar blues și, prin urmare, impuritatea sa Gini este dată și de,

G(dreapta) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Din calculul rapid, vedem că ambele ramuri stânga și dreapta ale împărțirii noastre perfecte au probabilități de 0 și, prin urmare, sunt într-adevăr perfecte. O impuritate Gini de 0 este cea mai mică și cea mai bună impuritate posibilă pentru orice set de date.

Împărțire imperfectă

În acest caz, ramura stângă are 5 roșii și 1 albastru. Impuritatea lui Gini poate fi dată de,

G(stânga) =1/6 ∗ (1−1/6) + 5/6 ∗ (1−5/6) = 0,278

Ramura dreaptă are tot albastrul și, prin urmare, așa cum a fost calculat mai sus, Impuritatea Gini este dată de,

G(dreapta) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Acum că avem Impuritățile Gini ale scindării imperfecte, pentru a evalua calitatea sau amploarea scindării, vom acorda o pondere specifică impurității fiecărei ramuri cu numărul de elemente pe care o are.

(0,6 ∗ 0,278) + (0,4 ∗ 0) = 0,167

Acum că am calculat indicele Gini, vom calcula valoarea unui alt parametru, Gini Gain și vom analiza aplicarea acestuia în Arborele de decizie. Cantitatea de impurități eliminate cu această împărțire este calculată prin scăderea valorii de mai sus cu indicele Gini pentru întregul set de date (0,5)

0,5 – 0,167 = 0,333

Această valoare calculată este numită „ Gini Gain ”. În termeni simpli, un câștig mai mare de Gini = o împărțire mai bună .

Prin urmare, într-un algoritm de arbore de decizie, cea mai bună împărțire este obținută prin maximizarea câștigului Gini, care este calculat în modul de mai sus cu fiecare iterație.

După calcularea câștigului Gini pentru fiecare atribut din setul de date, clasa sklearn.tree.DecisionTreeClassifier va alege cel mai mare câștig Gini ca nod rădăcină. Când se întâlnește o ramură cu Gini de 0, aceasta devine nodul frunzei, iar celelalte ramuri cu Gini mai mare de 0 necesită o divizare suplimentară. Aceste noduri sunt crescute recursiv până când toate sunt clasificate.

Utilizare în Machine Learning

Există diferiți algoritmi proiectați pentru scopuri diferite în lumea învățării automate. Problema constă în identificarea algoritmului care se potrivește cel mai bine unui anumit set de date. Algoritmul arborelui de decizie pare să arate și rezultate convingătoare. Pentru a o recunoaște, trebuie să ne gândim că arborii de decizie imită oarecum puterea subiectivă umană.

Deci, o problemă cu mai multe întrebări cognitive umane este probabil să fie mai potrivită pentru arbori de decizie. Conceptul de bază al arborilor de decizie poate fi ușor de înțeles pentru structura sa asemănătoare arborelui.

Citește și: Arborele de decizie în AI: Introducere, Tipuri și Creare

Concluzie

O alternativă la Indexul Gini este Entropia Informațională care a folosit pentru a determina care atribut ne oferă informații maxime despre o clasă. Se bazează pe conceptul de entropie, care este gradul de impuritate sau incertitudine. Acesta urmărește să scadă nivelul entropiei de la nodurile rădăcină la nodurile frunză ale arborelui de decizie.

În acest fel, indicele Gini este folosit de algoritmii CART pentru a optimiza arborii de decizie și pentru a crea puncte de decizie pentru arborii de clasificare.

Dacă sunteți interesat să aflați mai multe despre învățarea automată, consultați Diploma PG de la IIIT-B și upGrad în Învățare automată și AI, care este concepută pentru profesioniști care lucrează și oferă peste 450 de ore de pregătire riguroasă, peste 30 de studii de caz și sarcini, IIIT- B Statut de absolvenți, peste 5 proiecte practice practice și asistență pentru locuri de muncă cu firme de top.