Índice de Gini para árboles de decisión: mecanismo, división perfecta e imperfecta con ejemplos

Introducción

Decision Tree es uno de los enfoques prácticos más utilizados para el aprendizaje supervisado. Se puede utilizar para resolver tareas de regresión y clasificación y esta última se aplica más en la práctica. En estos árboles, las etiquetas de clase están representadas por las hojas y las ramas denotan las conjunciones de características que conducen a esas etiquetas de clase. Es ampliamente utilizado en algoritmos de aprendizaje automático. Por lo general, un enfoque de aprendizaje automático incluye el control de muchos hiperparámetros y optimizaciones.

El árbol de regresión se usa cuando el resultado pronosticado es un número real y el árbol de clasificación se usa para predecir la clase a la que pertenecen los datos. Estos dos términos se denominan colectivamente árboles de clasificación y regresión (CART).

Estas son técnicas de aprendizaje de árboles de decisión no paramétricos que proporcionan árboles de regresión o clasificación, dependiendo de si la variable dependiente es categórica o numérica, respectivamente. Este algoritmo despliega el método del Índice Gini para originar divisiones binarias. Tanto el índice de Gini como la impureza de Gini se usan indistintamente.

Los árboles de decisión han influido en los modelos de regresión en el aprendizaje automático. Mientras diseñaban el árbol, los desarrolladores establecieron las características de los nodos y los posibles atributos de esa característica con bordes.

Cálculo

El Índice de Gini o Impureza de Gini se calcula restando de uno la suma de las probabilidades al cuadrado de cada clase. Prefiere principalmente las particiones más grandes y son muy simples de implementar. En términos simples, calcula la probabilidad de que cierta característica seleccionada al azar se haya clasificado incorrectamente.

El Índice de Gini varía entre 0 y 1, donde 0 representa la pureza de la clasificación y 1 denota una distribución aleatoria de elementos entre varias clases. Un índice de Gini de 0,5 muestra que existe una distribución equitativa de elementos en algunas clases.

Matemáticamente, el Índice Gini está representado por

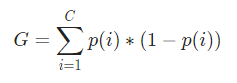
El índice de Gini funciona con variables categóricas y brinda los resultados en términos de "éxito" o "fracaso" y, por lo tanto, solo realiza una división binaria. No es computacionalmente intensivo como su contraparte, la ganancia de información. A partir del Índice de Gini, se calcula el valor de otro parámetro denominado Ganancia de Gini, cuyo valor se maximiza con cada iteración mediante el Árbol de decisión para obtener el CART perfecto

Entendamos el cálculo del Índice Gini con un ejemplo simple. En esto, tenemos un total de 10 puntos de datos con dos variables, los rojos y los azules. Los ejes X e Y están numerados con espacios de 100 entre cada término. A partir del ejemplo dado, calcularemos el Índice Gini y la Ganancia Gini.

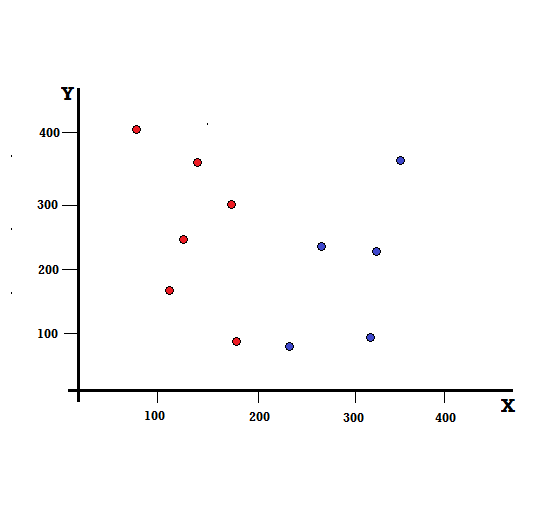
Para un árbol de decisión, necesitamos dividir el conjunto de datos en dos ramas. Considere los siguientes puntos de datos con 5 rojos y 5 azules marcados en el plano XY. Supongamos que hacemos una división binaria en X=200, entonces tendremos una división perfecta como se muestra a continuación.

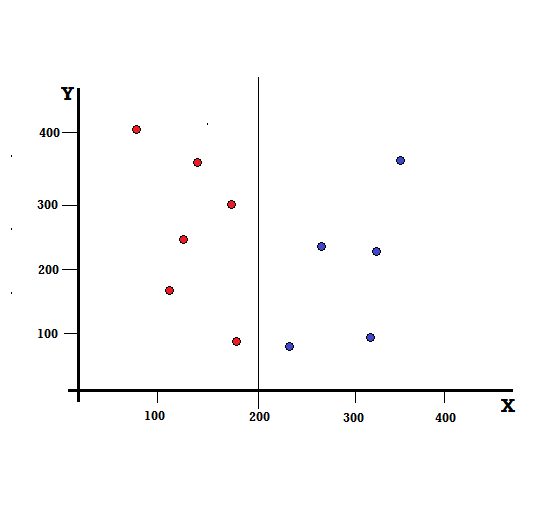
Se ve que el split se realiza correctamente y nos quedan dos ramas cada una con 5 rojas (rama izquierda) y 5 azules (rama derecha).

Pero, ¿cuál será el resultado si hacemos la división en X=250?

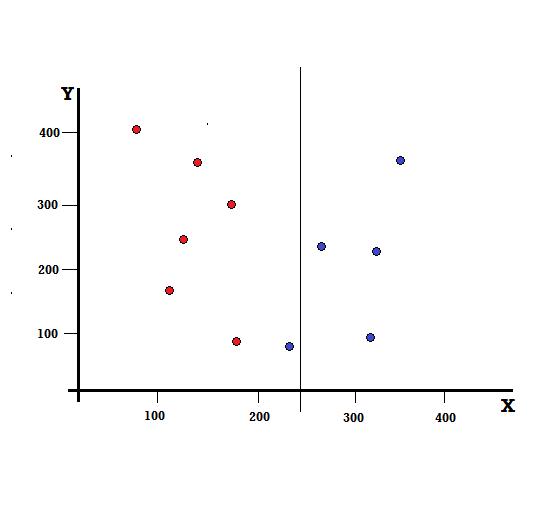
Nos quedan dos ramas, la rama izquierda consta de 5 rojos y 1 azul, mientras que la rama derecha consta de 4 azules. Lo siguiente se conoce como división imperfecta. Al entrenar el modelo del árbol de decisiones, para cuantificar la cantidad de imperfecciones de la división, podemos usar el índice de Gini.

Pago: Tipos de árbol binario

Mecanismo Básico

Para calcular la impureza de Gini , primero comprendamos su mecanismo básico.

• Primero, seleccionaremos aleatoriamente cualquier punto de datos del conjunto de datos
• Luego, lo clasificaremos aleatoriamente de acuerdo con la distribución de clases en el conjunto de datos dado. En nuestro conjunto de datos, daremos un punto de datos elegido con una probabilidad de 5/10 para el rojo y 5/10 para el azul, ya que hay cinco puntos de datos de cada color y, por lo tanto, la probabilidad.

Ahora, para calcular el índice de Gini, la fórmula está dada por

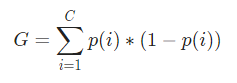
Donde, C es el número total de clases y p( i ) es la probabilidad de elegir el punto de datos con la clase i.

En el ejemplo anterior, tenemos C = 2 y p (1) = p (2) = 0.5, por lo tanto, el índice de Gini se puede calcular como,

G =p(1) ∗ (1−p(1)) + p(2) ∗ (1−p(2))

=0.5 ∗ (1−0.5) + 0.5 ∗ (1−0.5)

=0.5

Donde 0,5 es la probabilidad total de clasificar un punto de datos de manera imperfecta y, por lo tanto, es exactamente del 50 %.

Ahora, calculemos la impureza de Gini para la división perfecta e imperfecta que realizamos anteriormente,

división perfecta

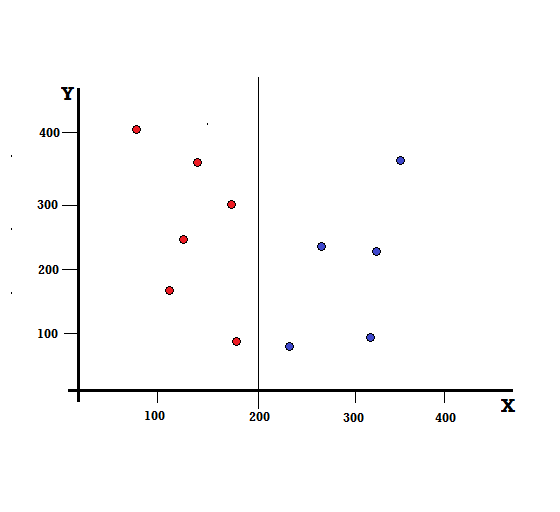
La rama izquierda solo tiene rojos y, por lo tanto, su impureza de Gini es,

G(izquierda) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

La rama derecha también tiene solo blues y, por lo tanto, su impureza de Gini también está dada por,

G(derecha) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

A partir del cálculo rápido, vemos que tanto la rama izquierda como la derecha de nuestra división perfecta tienen probabilidades de 0 y, por lo tanto, es perfecta. Una impureza de Gini de 0 es la impureza más baja y mejor posible para cualquier conjunto de datos.

división imperfecta

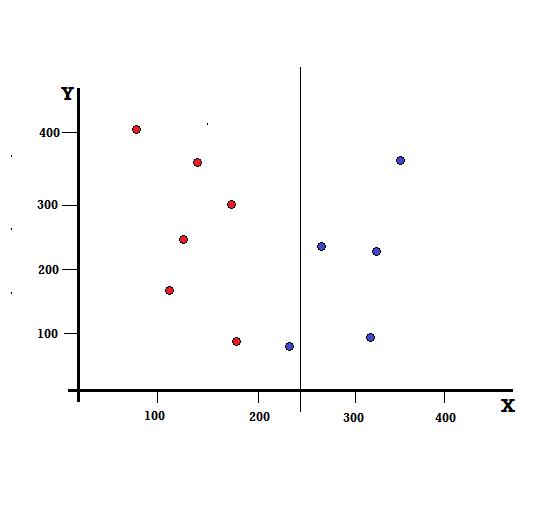
En este caso, la rama izquierda tiene 5 rojos y 1 azul. Su impureza de Gini puede estar dada por,

G(izquierda) =1/6 ∗ (1−1/6) + 5/6 ∗ (1−5/6) = 0,278

La rama derecha tiene todos los azules y, por lo tanto, como se calculó anteriormente, su impureza de Gini está dada por,

G(derecha) =1 ∗ (1−1) + 0 ∗ (1−0) = 0

Ahora que tenemos las Impurezas de Gini de la división imperfecta, para evaluar la calidad o extensión de la división, le daremos un peso específico a la impureza de cada rama con la cantidad de elementos que tiene.

(0,6 ∗ 0,278) + (0,4 ∗ 0) = 0,167

Ahora que hemos calculado el índice de Gini, calcularemos el valor de otro parámetro, la ganancia de Gini, y analizaremos su aplicación en los árboles de decisión. La cantidad de impureza eliminada con esta división se calcula deduciendo el valor anterior con el índice de Gini para todo el conjunto de datos (0,5)

0,5 – 0,167 = 0,333

Este valor calculado se denomina " Gini Gain ". En términos simples, mayor ganancia de Gini = mejor división .

Por lo tanto, en un algoritmo de árbol de decisión, la mejor división se obtiene maximizando la ganancia de Gini, que se calcula de la manera anterior con cada iteración.

Después de calcular la ganancia de Gini para cada atributo en el conjunto de datos, la clase, sklearn.tree.DecisionTreeClassifier elegirá la ganancia de Gini más grande como el nodo raíz. Cuando se encuentra una rama con Gini de 0, se convierte en el nodo hoja y las otras ramas con Gini superior a 0 necesitan una división adicional. Estos nodos crecen recursivamente hasta clasificarlos todos.

Uso en aprendizaje automático

Existen varios algoritmos diseñados para diferentes propósitos en el mundo del aprendizaje automático. El problema radica en identificar qué algoritmo se adapta mejor a un conjunto de datos determinado. El algoritmo del árbol de decisiones también parece mostrar resultados convincentes. Para reconocerlo, uno debe pensar que los árboles de decisión imitan un poco el poder subjetivo humano.

Por lo tanto, es probable que un problema con más preguntas cognitivas humanas sea más adecuado para los árboles de decisión. El concepto subyacente de árboles de decisión puede ser fácilmente comprensible por su estructura similar a un árbol.

Lea también: Árbol de decisiones en IA: Introducción, tipos y creación

Conclusión

Una alternativa al índice de Gini es la entropía de la información, que se usa para determinar qué atributo nos brinda la máxima información sobre una clase. Se basa en el concepto de entropía, que es el grado de impureza o incertidumbre. Su objetivo es disminuir el nivel de entropía desde los nodos raíz hasta los nodos hoja del árbol de decisión.

De esta forma, el índice de Gini es utilizado por los algoritmos CART para optimizar los árboles de decisión y crear puntos de decisión para los árboles de clasificación.

Si está interesado en obtener más información sobre el aprendizaje automático, consulte el Diploma PG en aprendizaje automático e IA de IIIT-B y upGrad, que está diseñado para profesionales que trabajan y ofrece más de 450 horas de capacitación rigurosa, más de 30 estudios de casos y asignaciones, IIIT- B Estado de exalumno, más de 5 proyectos prácticos finales prácticos y asistencia laboral con las mejores empresas.