Makine Öğrenimi İçin En İyi 10 Boyut Azaltma Tekniği

Her saniye, dünya benzeri görülmemiş bir veri hacmi üretiyor. Veriler, tüm sektörlerde işletmelerin ve kuruluşların önemli bir bileşeni haline geldiğinden, büyük veri kümelerinden anlamlı içgörüler elde etmek için bunları uygun şekilde işlemek, analiz etmek ve görselleştirmek çok önemlidir. Ancak, bir yakalama var - daha fazlası her zaman üretken ve doğru anlamına gelmez. Her saniye ne kadar çok veri üretirsek, onu analiz etmek ve geçerli çıkarımlar yapmak için görselleştirmek o kadar zor olur.

Boyutsallık Azaltma burada devreye giriyor.

Boyut Azaltma Nedir?

Basit bir deyişle, boyutsallık azaltma , bir veri özellik setinin boyutunu azaltma tekniğini ifade eder. Genellikle, makine öğrenimi veri kümeleri (özellik kümesi), üç boyutlu bir alanda büyük bir küre oluşturan yüzlerce sütun (yani özellikler) veya bir dizi nokta içerir. Boyut azaltma uygulayarak, sütun sayısını ölçülebilir sayılara indirebilir veya azaltabilir, böylece üç boyutlu küreyi iki boyutlu bir nesneye (daire) dönüştürebilirsiniz.

Şimdi soru geliyor, neden bir veri kümesindeki sütunları doğrudan bir ML algoritmasına besleyebildiğiniz ve her şeyi kendi başına çözmesine izin verdiğinizde neden azaltmalısınız?

Boyutluluk laneti, boyutluluk indirgeme uygulamasını zorunlu kılar.

Boyutluluğun Laneti

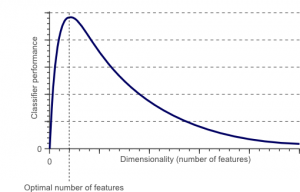
Boyutluluk laneti, düşük boyutlu uzaylarda var olmayan yüksek boyutlu uzaylarda verilerle çalıştığınızda (analiz edip görselleştirdiğinizde) ortaya çıkan bir olgudur.

Kaynak

Bir özellik setindeki özelliklerin veya faktörlerin (diğer bir deyişle değişkenler) sayısı ne kadar yüksekse, eğitim setini görselleştirmek ve üzerinde çalışmak o kadar zor hale gelir. Dikkate alınması gereken bir diğer önemli nokta, değişkenlerin çoğunun genellikle birbiriyle ilişkili olmasıdır. Dolayısıyla, özellik kümesi içindeki her değişkeni düşünürseniz, eğitim kümesine birçok gereksiz faktörü dahil edeceksiniz.

Ayrıca, elinizde ne kadar çok değişken varsa, örnekteki tüm olası özellik değerleri kombinasyonlarını temsil edecek örnek sayısı o kadar yüksek olacaktır. Değişken sayısı arttığında, model daha karmaşık hale gelecek ve böylece fazla uydurma olasılığı artacaktır. Bir ML modelini birçok özellik içeren büyük bir veri kümesi üzerinde eğittiğinizde, eğitim verilerine bağlı olması zorunludur. Bu, gerçek veriler üzerinde iyi performans göstermeyen, fazla takılmış bir modelle sonuçlanacaktır.

Boyut azaltmanın birincil amacı, fazla sığdırmaktan kaçınmaktır. Önemli ölçüde daha az özelliklere sahip bir eğitim verisi, modelinizin basit kalmasını sağlar – daha küçük varsayımlar yapar.

Bunun dışında, boyutsallık azaltmanın aşağıdakiler gibi birçok başka faydası vardır:

• Gürültüyü ve gereksiz özellikleri ortadan kaldırır.
• Modelin doğruluğunu ve performansını artırmaya yardımcı olur.
• Daha önemli boyutlar için uygun olmayan algoritmaların kullanımını kolaylaştırır.
• Gereken depolama alanı miktarını azaltır (daha az veri, daha az depolama alanı gerektirir).
• Verileri sıkıştırarak hesaplama süresini azaltır ve verilerin daha hızlı eğitilmesini kolaylaştırır.

Okuyun: Doğrusal diskriminant analizi nedir

Boyut Azaltma Teknikleri

Boyut azaltma teknikleri iki geniş kategoriye ayrılabilir:

1. Özellik seçimi

Özellik seçim yöntemi, orijinal veri kümesinden girdi değişkenlerinin (en alakalı olan) bir alt kümesini bulmayı amaçlar. Özellik seçimi üç strateji içerir:

• Filtre stratejisi
• sarma stratejisi
• Gömülü strateji

2. Özellik çıkarma

Özellik çıkarma, aka, özellik projeksiyonu, verileri yüksek boyutlu uzaydan daha küçük boyutlu bir alana dönüştürür. Bu veri dönüşümü doğrusal olabileceği gibi doğrusal olmayan da olabilir. Bu teknik, her biri girdi değişkenlerinin bir kombinasyonu olan (giriş değişkenleriyle aynı bilgiyi içeren) daha küçük yeni değişkenler kümesi bulur.

Lafı daha fazla uzatmadan, yaygın olarak kullanılan birkaç boyutsallık azaltma tekniğinin ayrıntılı bir tartışmasına geçelim!

1. Temel Bileşen Analizi (PCA)

Temel Bileşen Analizi, boyutsallık azaltmanın önde gelen doğrusal tekniklerinden biridir. Bu yöntem, düşük boyutlu gösterimde verilerin varyansını en üst düzeye çıkaracak şekilde verilerin daha küçük boyutlu bir uzaya doğrudan eşlenmesini gerçekleştirir.

Temel olarak, bir veri kümesinin ' n' koordinatlarını temel bileşenler olarak bilinen yeni bir n koordinat kümesine dikey olarak dönüştüren istatistiksel bir prosedürdür . Bu dönüştürme, maksimum varyansa sahip ilk ana bileşenin yaratılmasıyla sonuçlanır. Birbirini takip eden her bir temel bileşen, önceki bileşenlerle ortogonal (ilişkilendirilmemiş) olması koşuluyla, mümkün olan en yüksek varyansı taşır.

PCA dönüşümü, orijinal değişkenlerin göreli ölçeklenmesine duyarlıdır. Bu nedenle, PCA yöntemini uygulamadan önce veri sütunu aralıkları normalleştirilmelidir. Hatırlanması gereken başka bir şey de, PCA yaklaşımını kullanmanın veri kümenizin yorumlanabilirliğini kaybetmesine neden olacağıdır. Dolayısıyla, yorumlanabilirlik analiziniz için çok önemliyse, PCA projeniz için doğru boyut azaltma yöntemi değildir.

2. Negatif olmayan matris çarpanlara ayırma (NMF)

NMF, negatif olmayan bir matrisi, negatif olmayan iki matrisin ürününe ayırır. Bu, NMF yöntemini öncelikle negatif olmayan sinyallerle (örneğin astronomi) ilgilenen alanlarda değerli bir araç yapan şeydir. Lee & Seung'un çarpımsal güncelleme kuralı, belirsizlikleri dahil ederek, eksik verileri ve paralel hesaplamayı ve sıralı yapıyı dikkate alarak NMF tekniğini geliştirdi.

Bu kapanımlar, NMF yaklaşımını istikrarlı ve doğrusal hale getirmeye katkıda bulundu. PCA'dan farklı olarak NMF, matrislerin ortalamasını ortadan kaldırmaz, böylece fiziksel olmayan negatif olmayan akılar yaratır. Böylece NMF, PCA yönteminden daha fazla bilgi saklayabilir.

Sıralı NMF, inşaat sırasında sabit bir bileşen tabanı ve doğrusal bir modelleme süreci ile karakterize edilir. Bu onu astronomide mükemmel bir araç yapar. Sıralı NMF, ötegezegenlerin saptanması ve çevresel disklerin doğrudan görüntülenmesi gibi astronomideki çevresel yapıların doğrudan görüntülenmesindeki akışı koruyabilir.

3. Lineer diskriminant analizi (LDA)

Lineer diskriminant analizi, Fisher'in istatistik, örüntü tanıma ve makine öğreniminde yaygın olarak uygulanan lineer diskriminant yönteminin bir genellemesidir. LDA tekniği, iki veya daha fazla nesne sınıfını karakterize edebilen veya ayırt edebilen özelliklerin doğrusal bir kombinasyonunu bulmayı amaçlar. LDA, verileri sınıf ayrılabilirliğini en üst düzeye çıkaracak şekilde temsil eder. Aynı sınıfa ait nesneler izdüşüm yoluyla yan yana getirilirken, farklı sınıflara ait nesneler birbirinden uzakta düzenlenir.

4. Genelleştirilmiş diskriminant analizi (GDA)

Genelleştirilmiş diskriminant analizi, çekirdek fonksiyon operatöründen yararlanan doğrusal olmayan bir diskriminant analizidir. Temel teorisi, destek vektör makinelerinin (SVM) teorisiyle çok yakından eşleşir, öyle ki GDA tekniği, girdi vektörlerini yüksek boyutlu özellik uzayına eşlemeye yardımcı olur. LDA yaklaşımı gibi, GDA da sınıflar arası dağılımların sınıf içi dağılıma oranını maksimize ederek daha düşük boyutlu bir uzaydaki değişkenler için bir izdüşüm bulmaya çalışır.

5. Eksik Değer Oranı

Belirli bir veri kümesini incelediğinizde, veri kümesinde bazı eksik değerler olduğunu görebilirsiniz. Eksik değerlerle uğraşmanın ilk adımı, bunların arkasındaki nedeni belirlemektir. Buna göre, daha sonra eksik değerleri empoze edebilir veya uygun yöntemleri kullanarak bunları tamamen bırakabilirsiniz. Bu yaklaşım, birkaç eksik değerin olduğu durumlar için mükemmeldir.

Ancak, örneğin %50'nin üzerinde çok fazla eksik değer olduğunda ne yapılmalı? Bu gibi durumlarda eşik değeri belirleyip kayıp değerler oran yöntemini kullanabilirsiniz. Eşik değeri ne kadar yüksek olursa, boyutsallık azaltma o kadar agresif olacaktır. Bir değişkendeki eksik değerlerin yüzdesi eşiği aşarsa, değişkeni bırakabilirsiniz.

Genel olarak, çok sayıda eksik değere sahip veri sütunları, neredeyse hiç yararlı bilgi içermez. Böylece, ayarlanan eşikten daha yüksek eksik değerlere sahip tüm veri sütunlarını kaldırabilirsiniz.

6. Düşük Varyans Filtresi

Eksik değişkenler için kayıp değerler oranı yöntemini kullandığınız gibi, sabit değişkenler için de düşük varyans filtresi tekniği vardır. Bir veri kümesinin sabit değişkenleri olduğunda, modelin performansını iyileştirmek mümkün değildir. Niye ya? Çünkü varyansı sıfırdır.

Bu yöntemde ayrıca, tüm sabit değişkenleri ortadan kaldırmak için bir eşik değeri belirleyebilirsiniz. Böylece eşik değerinden daha düşük varyansa sahip tüm veri sütunları elenecektir. Ancak, düşük varyanslı filtre yöntemi hakkında hatırlamanız gereken bir şey varyansın aralığa bağlı olduğudur. Bu nedenle, bu boyutluluk azaltma tekniğini uygulamadan önce normalleştirme bir zorunluluktur.

7. Yüksek Korelasyon Filtresi

Bir veri kümesi, çok sayıda benzer örüntü/eğilim içeren veri sütunlarından oluşuyorsa, bu veri sütunlarının aynı bilgileri içerme olasılığı yüksektir. Ayrıca, daha yüksek bir korelasyon gösteren boyutlar, modelin performansını olumsuz etkileyebilir. Böyle bir durumda, ML modelini beslemek için bu değişkenlerden biri yeterlidir.

Bu gibi durumlarda, yüksek korelasyon gösteren değişkenleri belirlemek için Pearson korelasyon matrisini kullanmak en iyisidir. Belirlendiklerinde, VIF (Varyans Enflasyon Faktörü) kullanarak bunlardan birini seçebilirsiniz. Daha yüksek bir değere sahip tüm değişkenleri kaldırabilirsiniz ( VIF > 5 ). Bu yaklaşımda, sayısal sütunlar ( Pearson'ın Ürün Moment Katsayısı ) ve nominal sütunlar ( Pearson'ın ki-kare değeri ) arasındaki korelasyon katsayısını hesaplamanız gerekir . Burada, ayarlanan eşikten daha yüksek bir korelasyon katsayısına sahip olan tüm sütun çiftleri 1'e düşürülecektir.

Korelasyon ölçeğe duyarlı olduğundan, sütun normalleştirmesi yapmanız gerekir.

8. Geriye Doğru Özellik Eliminasyonu

Geriye dönük özellik eleme tekniğinde, tüm 'n' boyutlarıyla başlamanız gerekir. Böylece, belirli bir yinelemede, belirli bir sınıflandırma algoritmasının n giriş özelliği üzerinde eğitilmesini sağlayabilirsiniz . Şimdi, her seferinde bir girdi özelliğini kaldırmanız ve aynı modeli n-1 girdi değişkeni üzerinde n kez eğitmeniz gerekiyor. Ardından, ortadan kaldırılması hata oranında en küçük artışı sağlayan ve n-1 girdi özelliklerini geride bırakan girdi değişkenini kaldırırsınız . Ayrıca, n-2 özelliklerini kullanarak sınıflandırmayı tekrarlarsınız ve bu, başka hiçbir değişken kaldırılamayana kadar devam eder.

Her yineleme ( k) , e(k) hata oranına sahip nk özellikleri üzerinde eğitilmiş bir model oluşturur . Bunu takiben, verilen ML algoritması ile bu sınıflandırma performansına ulaşmak için gereken en az sayıda özelliği tanımlamak için maksimum katlanılabilir hata oranını seçmelisiniz.

Ayrıca Okuyun: İş Hayatında Veri Analizi Neden Önemlidir?

9. İleri Özellik Yapısı

İleri özellik oluşturma, geriye dönük özellik eleme yönteminin tersidir. İleri özellik oluşturma yönteminde, bir özellik ile başlarsınız ve her seferinde bir özellik ekleyerek ilerlemeye devam edersiniz (bu, performansta en büyük artışı sağlayan değişkendir).

Hem ileriye dönük özellik oluşturma hem de geriye dönük özellik ortadan kaldırma, zaman ve hesaplama açısından yoğundur. Bu yöntemler, zaten az sayıda giriş sütunu olan veri kümeleri için en uygun yöntemdir.

10. Rastgele Ormanlar

Rastgele ormanlar sadece mükemmel sınıflandırıcılar değil, aynı zamanda özellik seçimi için de son derece kullanışlıdır. Bu boyutluluk azaltma yaklaşımında, bir hedef özniteliğe karşı dikkatli bir şekilde kapsamlı bir ağaç ağı oluşturmalısınız. Örneğin, her ağacın toplam öznitelik sayısının küçük bir bölümü (3) üzerinde eğitildiği geniş bir sığ ağaç kümesi (örneğin, 2000) oluşturabilirsiniz (örneğin, iki düzeyi vardır).

Amaç, özelliklerin en bilgilendirici alt kümesini belirlemek için her bir özniteliğin kullanım istatistiklerini kullanmaktır. Bir özniteliğin en iyi bölünme olduğu tespit edilirse, genellikle dikkate alınmaya değer bilgilendirici bir özellik içerir. Rastgele ormandaki bir özniteliğin kullanım istatistiklerinin diğer özniteliklere göre puanını hesapladığınızda, size en öngörülü öznitelikleri verir.

Çözüm

Sonuç olarak, boyut indirgeme söz konusu olduğunda, hiçbir teknik mutlak olarak en iyisi değildir. Her birinin tuhaflıkları ve avantajları vardır. Bu nedenle, boyut azaltma tekniklerini uygulamanın en iyi yolu, modelinizde hangi tekniğin/tekniklerin işe yaradığını ve hangilerinin belirli bir veri kümesinde en iyi performansı sağladığını bulmak için sistematik ve kontrollü deneyler kullanmaktır.

Makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, çalışan profesyoneller için tasarlanmış ve 450+ saat zorlu eğitim, 30'dan fazla vaka çalışması ve ödev, IIIT- sunan IIIT-B & upGrad'ın Makine Öğrenimi ve Yapay Zeka PG Diplomasına göz atın. B Mezun statüsü, 5+ pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.