Top 10 des techniques de réduction de dimensionnalité pour l'apprentissage automatique

Chaque seconde, le monde génère un volume de données sans précédent. Comme les données sont devenues un élément crucial des entreprises et des organisations dans tous les secteurs, il est essentiel de les traiter, de les analyser et de les visualiser de manière appropriée pour extraire des informations significatives à partir de grands ensembles de données. Cependant, il y a un hic – plus ne signifie pas toujours productif et précis. Plus nous produisons de données chaque seconde, plus il est difficile de les analyser et de les visualiser pour en tirer des conclusions valables.

C'est là que la réduction de dimensionnalité entre en jeu.

Qu'est-ce que la réduction de dimensionnalité ?

En termes simples, la réduction de la dimensionnalité fait référence à la technique de réduction de la dimension d'un ensemble de caractéristiques de données. Habituellement, les ensembles de données d'apprentissage automatique (ensemble de fonctionnalités) contiennent des centaines de colonnes (c'est-à-dire des fonctionnalités) ou un tableau de points, créant une sphère massive dans un espace tridimensionnel. En appliquant la réduction de dimensionnalité , vous pouvez diminuer ou réduire le nombre de colonnes à des nombres quantifiables, transformant ainsi la sphère tridimensionnelle en un objet bidimensionnel (cercle).

Vient maintenant la question, pourquoi devez-vous réduire les colonnes d'un ensemble de données alors que vous pouvez l'alimenter directement dans un algorithme ML et le laisser tout faire par lui-même ?

La malédiction de la dimensionnalité rend obligatoire l'application de la réduction de la dimensionnalité .

La malédiction de la dimensionnalité

La malédiction de la dimensionnalité est un phénomène qui survient lorsque vous travaillez (analysez et visualisez) avec des données dans des espaces de grande dimension qui n'existent pas dans des espaces de faible dimension.

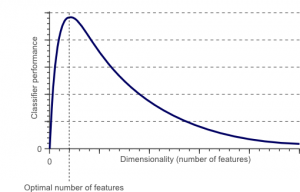
La source

Plus le nombre de fonctionnalités ou de facteurs (alias variables) dans un ensemble de fonctionnalités est élevé, plus il devient difficile de visualiser l'ensemble d'apprentissage et de travailler dessus. Un autre point essentiel à considérer est que la plupart des variables sont souvent corrélées. Ainsi, si vous pensez à chaque variable dans l'ensemble de fonctionnalités, vous inclurez de nombreux facteurs redondants dans l'ensemble de formation.

De plus, plus vous avez de variables à portée de main, plus le nombre d'échantillons pour représenter toutes les combinaisons possibles de valeurs de caractéristiques dans l'exemple sera élevé. Lorsque le nombre de variables augmente, le modèle devient plus complexe, augmentant ainsi la probabilité de surajustement. Lorsque vous formez un modèle ML sur un grand ensemble de données contenant de nombreuses fonctionnalités, il dépend forcément des données de formation. Cela se traduira par un modèle surajusté qui ne fonctionne pas bien sur des données réelles.

L'objectif principal de la réduction de la dimensionnalité est d'éviter le surajustement. Des données d'entraînement avec des fonctionnalités considérablement moindres garantiront que votre modèle reste simple - il fera des hypothèses plus petites.

En dehors de cela, la réduction de la dimensionnalité présente de nombreux autres avantages, tels que :

• Il élimine le bruit et les fonctionnalités redondantes.
• Cela permet d'améliorer la précision et les performances du modèle.
• Il facilite l'utilisation d'algorithmes inadaptés à des dimensions plus substantielles.
• Il réduit la quantité d'espace de stockage nécessaire (moins de données nécessitent moins d'espace de stockage).
• Il compresse les données, ce qui réduit le temps de calcul et facilite un apprentissage plus rapide des données.

Lire : Qu'est-ce que l'analyse discriminante linéaire ?

Techniques de réduction de la dimensionnalité

Les techniques de réduction de la dimensionnalité peuvent être classées en deux grandes catégories :

1. Sélection des fonctionnalités

La méthode de sélection des caractéristiques vise à trouver un sous-ensemble des variables d'entrée (les plus pertinentes) à partir de l'ensemble de données d'origine. La sélection des fonctionnalités comprend trois stratégies, à savoir :

• Stratégie de filtrage
• Stratégie d'emballage
• Stratégie embarquée

2. Extraction de fonctionnalités

L'extraction de caractéristiques, également appelée projection de caractéristiques, convertit les données de l'espace de grande dimension en un espace de dimensions inférieures. Cette transformation de données peut être soit linéaire, soit non linéaire également. Cette technique trouve un plus petit ensemble de nouvelles variables, dont chacune est une combinaison de variables d'entrée (contenant les mêmes informations que les variables d'entrée).

Sans plus tarder, plongeons dans une discussion détaillée de quelques techniques de réduction de dimensionnalité couramment utilisées !

1. Analyse en composantes principales (ACP)

L'analyse en composantes principales est l'une des principales techniques linéaires de réduction de la dimensionnalité. Cette méthode effectue un mappage direct des données sur un espace de dimension inférieure d'une manière qui maximise la variance des données dans la représentation de faible dimension.

Il s'agit essentiellement d'une procédure statistique qui convertit orthogonalement les coordonnées « n » d'un ensemble de données en un nouvel ensemble de coordonnées n , appelées composantes principales. Cette conversion aboutit à la création de la première composante principale ayant la variance maximale. Chaque composante principale suivante porte la variance la plus élevée possible, à condition qu'elle soit orthogonale (non corrélée) aux composantes précédentes.

La conversion PCA est sensible à la mise à l'échelle relative des variables d'origine. Ainsi, les plages de colonnes de données doivent d'abord être normalisées avant de mettre en œuvre la méthode PCA. Une autre chose à retenir est que l'utilisation de l'approche PCA fera perdre à votre ensemble de données son interprétabilité. Ainsi, si l'interprétabilité est cruciale pour votre analyse, l'ACP n'est pas la bonne méthode de réduction de dimensionnalité pour votre projet.

2. Factorisation matricielle non négative (NMF)

NMF décompose une matrice non négative en le produit de deux matrices non négatives. C'est ce qui fait de la méthode NMF un outil précieux dans les domaines principalement concernés par les signaux non négatifs (par exemple, l'astronomie). La règle de mise à jour multiplicative de Lee & Seung a amélioré la technique NMF en incluant les incertitudes, en tenant compte des données manquantes et du calcul parallèle, et de la construction séquentielle.

Ces inclusions ont contribué à rendre l'approche NMF stable et linéaire. Contrairement à PCA, NMF n'élimine pas la moyenne des matrices, créant ainsi des flux non physiques non négatifs. Ainsi, NMF peut conserver plus d'informations que la méthode PCA.

La NMF séquentielle se caractérise par une base de composants stable pendant la construction et un processus de modélisation linéaire. Cela en fait l'outil parfait en astronomie. La NMF séquentielle peut préserver le flux dans l'imagerie directe des structures circumstellaires en astronomie, comme la détection d'exoplanètes et l'imagerie directe des disques circumstellaires.

3. Analyse discriminante linéaire (LDA)

L'analyse discriminante linéaire est une généralisation de la méthode discriminante linéaire de Fisher qui est largement appliquée dans les statistiques, la reconnaissance de formes et l'apprentissage automatique. La technique LDA vise à trouver une combinaison linéaire de caractéristiques qui peuvent caractériser ou différencier deux ou plusieurs classes d'objets. LDA représente les données d'une manière qui maximise la séparabilité des classes. Alors que des objets appartenant à une même classe sont juxtaposés par projection, des objets de classes différentes sont disposés à distance.

4. Analyse discriminante généralisée (GDA)

L'analyse discriminante généralisée est une analyse discriminante non linéaire qui exploite l'opérateur de la fonction noyau. Sa théorie sous-jacente correspond très étroitement à celle des machines à vecteurs de support (SVM), de sorte que la technique GDA aide à cartographier les vecteurs d'entrée dans un espace de caractéristiques de grande dimension. Tout comme l'approche LDA, GDA cherche également à trouver une projection pour les variables dans un espace de dimension inférieure en maximisant le rapport des dispersions inter-classes à la dispersion intra-classe.

5. Ratio des valeurs manquantes

Lorsque vous explorez un jeu de données donné, vous pouvez constater qu'il y a des valeurs manquantes dans le jeu de données. La première étape dans le traitement des valeurs manquantes consiste à identifier la raison qui les sous-tend. En conséquence, vous pouvez ensuite imputer les valeurs manquantes ou les supprimer complètement en utilisant les méthodes appropriées. Cette approche est parfaite pour les situations où il y a quelques valeurs manquantes.

Cependant, que faire lorsqu'il y a trop de valeurs manquantes, disons, plus de 50 % ? Dans de telles situations, vous pouvez définir une valeur seuil et utiliser la méthode du ratio des valeurs manquantes. Plus la valeur seuil est élevée, plus la réduction de dimensionnalité sera agressive. Si le pourcentage de valeurs manquantes dans une variable dépasse le seuil, vous pouvez supprimer la variable.

Généralement, les colonnes de données ayant de nombreuses valeurs manquantes ne contiennent guère d'informations utiles. Ainsi, vous pouvez supprimer toutes les colonnes de données ayant des valeurs manquantes supérieures au seuil défini.

6. Filtre à faible variance

Tout comme vous utilisez la méthode du rapport des valeurs manquantes pour les variables manquantes, il existe la technique du filtre à faible variance pour les variables constantes. Lorsqu'un jeu de données a des variables constantes, il n'est pas possible d'améliorer les performances du modèle. Pourquoi? Parce qu'il a une variance nulle.

Dans cette méthode également, vous pouvez définir une valeur seuil pour sevrer toutes les variables constantes. Ainsi, toutes les colonnes de données dont la variance est inférieure à la valeur seuil seront éliminées. Cependant, une chose que vous devez retenir à propos de la méthode du filtre à faible variance est que la variance dépend de la plage. Ainsi, la normalisation est un must avant de mettre en œuvre cette technique de réduction de dimensionnalité.

7. Filtre à haute corrélation

Si un ensemble de données se compose de colonnes de données ayant de nombreux modèles/tendances similaires, ces colonnes de données sont très susceptibles de contenir des informations identiques. De plus, les dimensions qui présentent une corrélation plus élevée peuvent avoir un impact négatif sur les performances du modèle. Dans un tel cas, une de ces variables est suffisante pour alimenter le modèle ML.

Dans de telles situations, il est préférable d'utiliser la matrice de corrélation de Pearson pour identifier les variables présentant une corrélation élevée. Une fois qu'ils sont identifiés, vous pouvez en sélectionner un à l'aide du VIF (Variance Inflation Factor). Vous pouvez supprimer toutes les variables ayant une valeur supérieure ( VIF > 5 ). Dans cette approche, vous devez calculer le coefficient de corrélation entre les colonnes numériques ( coefficient de moment du produit de Pearson ) et entre les colonnes nominales ( valeur du chi carré de Pearson ). Ici, tous les couples de colonnes ayant un coefficient de corrélation supérieur au seuil fixé seront réduits à 1.

Étant donné que la corrélation est sensible à l'échelle, vous devez effectuer une normalisation de colonne.

8. Élimination des fonctionnalités en arrière

Dans la technique d'élimination des caractéristiques vers l'arrière, vous devez commencer avec toutes les "n" dimensions. Ainsi, à une itération donnée, vous pouvez entraîner un algorithme de classification spécifique sur n caractéristiques d'entrée. Maintenant, vous devez supprimer une caractéristique d'entrée à la fois et former le même modèle sur n-1 variables d'entrée n fois. Ensuite, vous supprimez la variable d'entrée dont l'élimination génère la plus petite augmentation du taux d'erreur, ce qui laisse n-1 caractéristiques d'entrée. De plus, vous répétez la classification en utilisant n-2 fonctionnalités, et cela continue jusqu'à ce qu'aucune autre variable ne puisse être supprimée.

Chaque itération ( k) crée un modèle entraîné sur nk caractéristiques ayant un taux d'erreur de e(k) . Ensuite, vous devez sélectionner le taux d'erreur maximal supportable pour définir le plus petit nombre de fonctionnalités nécessaires pour atteindre cette performance de classification avec l'algorithme ML donné.

Lisez aussi : Pourquoi l'analyse des données est importante dans les affaires

9. Construction de fonctionnalités avancées

La construction des caractéristiques vers l'avant est l'opposé de la méthode d'élimination des caractéristiques vers l'arrière. Dans la méthode de construction de fonctionnalités avancées, vous commencez avec une fonctionnalité et continuez à progresser en ajoutant une fonctionnalité à la fois (il s'agit de la variable qui entraîne la plus grande amélioration des performances).

La construction de caractéristiques vers l'avant et l'élimination des caractéristiques vers l'arrière demandent beaucoup de temps et de calculs. Ces méthodes conviennent mieux aux ensembles de données qui ont déjà un faible nombre de colonnes d'entrée.

10. Forêts aléatoires

Les forêts aléatoires ne sont pas seulement d'excellents classificateurs, elles sont également extrêmement utiles pour la sélection d'entités. Dans cette approche de réduction de la dimensionnalité, vous devez soigneusement construire un vaste réseau d'arbres par rapport à un attribut cible. Par exemple, vous pouvez créer un grand ensemble (par exemple, 2000) d'arbres peu profonds (par exemple, ayant deux niveaux), où chaque arbre est formé sur une fraction mineure (3) du nombre total d'attributs.

L'objectif est d'utiliser les statistiques d'utilisation de chaque attribut pour identifier le sous-ensemble de fonctionnalités le plus informatif. Si un attribut s'avère être le meilleur fractionnement, il contient généralement une caractéristique informative qui mérite d'être prise en considération. Lorsque vous calculez le score des statistiques d'utilisation d'un attribut dans la forêt aléatoire par rapport à d'autres attributs, cela vous donne les attributs les plus prédictifs.

Conclusion

Pour conclure, en matière de réduction de dimensionnalité, aucune technique n'est la meilleure absolue. Chacun a ses particularités et ses avantages. Ainsi, la meilleure façon de mettre en œuvre des techniques de réduction de la dimensionnalité consiste à utiliser des expériences systématiques et contrôlées pour déterminer quelle(s) technique(s) fonctionne(nt) avec votre modèle et laquelle offre les meilleures performances sur un ensemble de données donné.

Si vous souhaitez en savoir plus sur l'apprentissage automatique, consultez le diplôme PG en apprentissage automatique et IA de IIIT-B & upGrad, conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, IIIT- Statut B Alumni, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.