Top 10 der Dimensionsreduktionstechniken für maschinelles Lernen

Jede Sekunde generiert die Welt eine beispiellose Menge an Daten. Da Daten zu einem entscheidenden Bestandteil von Unternehmen und Organisationen in allen Branchen geworden sind, ist es unerlässlich, sie angemessen zu verarbeiten, zu analysieren und zu visualisieren, um aussagekräftige Erkenntnisse aus großen Datensätzen zu gewinnen. Es gibt jedoch einen Haken – mehr bedeutet nicht immer produktiv und genau. Je mehr Daten wir jede Sekunde produzieren, desto schwieriger ist es, sie zu analysieren und zu visualisieren, um gültige Schlussfolgerungen zu ziehen.

Hier kommt die Dimensionsreduktion ins Spiel.

Was ist Dimensionsreduktion?

In einfachen Worten bezieht sich Dimensionalitätsreduktion auf die Technik, die Dimension eines Datenmerkmalssatzes zu reduzieren. Normalerweise enthalten maschinelle Lerndatensätze (Feature-Set) Hunderte von Spalten (dh Features) oder eine Reihe von Punkten, wodurch eine riesige Kugel in einem dreidimensionalen Raum entsteht. Durch Anwenden der Dimensionalitätsreduktion können Sie die Anzahl der Spalten auf quantifizierbare Anzahl verringern oder reduzieren und dadurch die dreidimensionale Kugel in ein zweidimensionales Objekt (Kreis) umwandeln.

Nun stellt sich die Frage, warum muss man die Spalten in einem Datensatz reduzieren, wenn man ihn direkt in einen ML-Algorithmus einspeisen und ihn alles selbst erledigen lassen kann?

Der Fluch der Dimensionalität verlangt die Anwendung der Dimensionsreduktion .

Der Fluch der Dimensionalität

Der Fluch der Dimensionalität ist ein Phänomen, das entsteht, wenn man mit Daten in hochdimensionalen Räumen arbeitet (analysiert und visualisiert), die in niederdimensionalen Räumen nicht existieren.

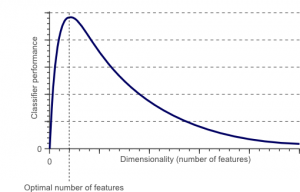
Quelle

Je höher die Anzahl der Merkmale oder Faktoren (auch bekannt als Variablen) in einem Merkmalssatz ist, desto schwieriger wird es, den Trainingssatz zu visualisieren und daran zu arbeiten. Ein weiterer wichtiger Punkt ist, dass die meisten Variablen oft korrelieren. Wenn Sie also jede Variable innerhalb des Funktionssatzes berücksichtigen, werden Sie viele redundante Faktoren in den Trainingssatz aufnehmen.

Je mehr Variablen Sie zur Hand haben, desto höher ist die Anzahl der Stichproben, um alle möglichen Kombinationen von Merkmalswerten im Beispiel darzustellen. Wenn die Anzahl der Variablen zunimmt, wird das Modell komplexer, wodurch die Wahrscheinlichkeit einer Überanpassung steigt. Wenn Sie ein ML-Modell mit einem großen Dataset trainieren, das viele Features enthält, ist es zwangsläufig von den Trainingsdaten abhängig. Dies führt zu einem überangepassten Modell, das bei realen Daten keine gute Leistung erbringt.

Das primäre Ziel der Dimensionalitätsreduktion ist die Vermeidung von Overfitting. Trainingsdaten mit deutlich geringeren Merkmalen sorgen dafür, dass Ihr Modell einfach bleibt – es werden weniger Annahmen getroffen.

Abgesehen davon hat die Dimensionsreduktion viele weitere Vorteile, wie zum Beispiel:

• Es eliminiert Rauschen und redundante Funktionen.
• Es hilft, die Genauigkeit und Leistung des Modells zu verbessern.
• Es erleichtert die Verwendung von Algorithmen, die für umfangreichere Dimensionen ungeeignet sind.
• Es reduziert den erforderlichen Speicherplatz (weniger Daten benötigen weniger Speicherplatz).
• Es komprimiert die Daten, was die Rechenzeit reduziert und ein schnelleres Training der Daten ermöglicht.

Lesen Sie: Was ist eine lineare Diskriminanzanalyse?

Techniken zur Dimensionsreduktion

Techniken zur Dimensionsreduktion können in zwei große Kategorien eingeteilt werden:

1. Funktionsauswahl

Die Merkmalsauswahlmethode zielt darauf ab, eine Teilmenge der Eingabevariablen (die am relevantesten sind) aus dem ursprünglichen Datensatz zu finden. Die Merkmalsauswahl umfasst drei Strategien, nämlich:

• Filterstrategie
• Wrapper-Strategie
• Eingebettete Strategie

2. Merkmalsextraktion

Merkmalsextraktion, auch bekannt als Merkmalsprojektion, wandelt die Daten aus dem hochdimensionalen Raum in einen mit geringeren Dimensionen um. Diese Datentransformation kann entweder linear oder auch nichtlinear sein. Diese Technik findet einen kleineren Satz neuer Variablen, von denen jede eine Kombination von Eingabevariablen ist (die dieselben Informationen wie die Eingabevariablen enthalten).

Lassen Sie uns ohne weiteres in eine detaillierte Diskussion einiger häufig verwendeter Techniken zur Reduzierung der Dimensionalität eintauchen!

1. Hauptkomponentenanalyse (PCA)

Die Hauptkomponentenanalyse ist eine der führenden linearen Techniken der Dimensionsreduktion. Dieses Verfahren führt eine direkte Zuordnung der Daten zu einem weniger dimensionalen Raum in einer Weise durch, die die Varianz der Daten in der niedrigdimensionalen Darstellung maximiert.

Im Wesentlichen handelt es sich um ein statistisches Verfahren, das die ' n' Koordinaten eines Datensatzes orthogonal in einen neuen Satz von n Koordinaten umwandelt, die als Hauptkomponenten bekannt sind. Diese Umrechnung führt zur Bildung der ersten Hauptkomponente mit der maximalen Varianz. Jede nachfolgende Hauptkomponente trägt die höchstmögliche Varianz, unter der Bedingung, dass sie orthogonal (nicht korreliert) zu den vorhergehenden Komponenten ist.

Die PCA-Konvertierung reagiert empfindlich auf die relative Skalierung der ursprünglichen Variablen. Daher müssen die Datenspaltenbereiche zuerst normalisiert werden, bevor das PCA-Verfahren implementiert wird. Eine andere Sache, die Sie beachten sollten, ist, dass die Verwendung des PCA-Ansatzes dazu führt, dass Ihr Datensatz seine Interpretierbarkeit verliert. Wenn also die Interpretierbarkeit für Ihre Analyse entscheidend ist, ist PCA nicht die richtige Methode zur Reduzierung der Dimensionalität für Ihr Projekt.

2. Nicht-negative Matrixfaktorisierung (NMF)

NMF zerlegt eine nicht negative Matrix in das Produkt zweier nicht negativer. Dies macht die NMF-Methode zu einem wertvollen Werkzeug in Bereichen, die sich hauptsächlich mit nicht-negativen Signalen befassen (z. B. Astronomie). Die multiplikative Aktualisierungsregel von Lee & Seung verbesserte die NMF-Technik um – Einbeziehung von Unsicherheiten, Berücksichtigung fehlender Daten und paralleler Berechnung und sequentieller Konstruktion.

Diese Einschlüsse trugen dazu bei, den NMF-Ansatz stabil und linear zu machen. Im Gegensatz zu PCA eliminiert NMF nicht den Mittelwert der Matrizen, wodurch unphysikalische nicht-negative Flüsse erzeugt werden. Somit kann NMF mehr Informationen bewahren als das PCA-Verfahren.

Sequentielles NMF zeichnet sich durch eine stabile Komponentenbasis während der Konstruktion und einen linearen Modellierungsprozess aus. Das macht es zum perfekten Werkzeug in der Astronomie. Sequential NMF kann den Fluss bei der direkten Abbildung zirkumstellarer Strukturen in der Astronomie bewahren, wie z. B. bei der Erkennung von Exoplaneten und der direkten Abbildung zirkumstellarer Scheiben.

3. Lineare Diskriminanzanalyse (LDA)

Die lineare Diskriminanzanalyse ist eine Verallgemeinerung der linearen Diskriminanzmethode von Fisher, die in der Statistik, Mustererkennung und beim maschinellen Lernen weit verbreitet ist. Die LDA-Technik zielt darauf ab, eine lineare Kombination von Merkmalen zu finden, die zwei oder mehr Klassen von Objekten charakterisieren oder zwischen ihnen unterscheiden können. LDA stellt Daten so dar, dass die Klassentrennbarkeit maximiert wird. Während Objekte derselben Klasse per Projektion nebeneinander gestellt werden, werden Objekte unterschiedlicher Klassen weit voneinander entfernt angeordnet.

4. Generalisierte Diskriminanzanalyse (GDA)

Die verallgemeinerte Diskriminanzanalyse ist eine nichtlineare Diskriminanzanalyse, die den Kernel-Funktionsoperator nutzt. Die zugrunde liegende Theorie stimmt sehr gut mit der von Support Vector Machines (SVM) überein, sodass die GDA-Technik hilft, die Eingabevektoren in einen hochdimensionalen Merkmalsraum abzubilden. Genau wie der LDA-Ansatz versucht auch GDA, eine Projektion für Variablen in einem niedrigerdimensionalen Raum zu finden, indem das Verhältnis von Streuungen zwischen Klassen zu Streuungen innerhalb von Klassen maximiert wird.

5. Verhältnis fehlender Werte

Wenn Sie ein bestimmtes Dataset durchsuchen, stellen Sie möglicherweise fest, dass einige Werte im Dataset fehlen. Der erste Schritt im Umgang mit fehlenden Werten besteht darin, den Grund dafür zu ermitteln. Dementsprechend können Sie dann die fehlenden Werte imputieren oder ganz weglassen, indem Sie die standesgemäßen Methoden anwenden. Dieser Ansatz ist perfekt für Situationen, in denen einige Werte fehlen.

Was aber tun, wenn zu viele fehlende Werte vorhanden sind, sagen wir über 50 %? In solchen Situationen können Sie einen Schwellenwert festlegen und die Missing-Values-Ratio-Methode verwenden. Je höher der Schwellenwert, desto aggressiver wird die Dimensionsreduktion sein. Wenn der Prozentsatz fehlender Werte in einer Variablen den Schwellenwert überschreitet, können Sie die Variable löschen.

Im Allgemeinen enthalten Datenspalten mit zahlreichen fehlenden Werten kaum nützliche Informationen. Sie können also alle Datenspalten mit fehlenden Werten entfernen, die höher als der festgelegte Schwellenwert sind.

6. Low-Varianz-Filter

So wie Sie die Methode des Verhältnisses fehlender Werte für fehlende Variablen verwenden, gibt es für konstante Variablen die Filtertechnik für niedrige Varianzen. Wenn ein Datensatz konstante Variablen enthält, ist es nicht möglich, die Leistung des Modells zu verbessern. Warum? Weil es null Varianz hat.

Auch bei dieser Methode können Sie einen Schwellenwert festlegen, um alle konstanten Variablen zu entwöhnen. Daher werden alle Datenspalten mit einer Varianz kleiner als der Schwellenwert eliminiert. Eine Sache, die Sie bei der Filtermethode mit niedriger Varianz beachten müssen, ist jedoch, dass die Varianz bereichsabhängig ist. Daher ist eine Normalisierung ein Muss, bevor diese Technik zur Reduzierung der Dimensionalität implementiert wird.

7. Hoher Korrelationsfilter

Wenn ein Datensatz aus Datenspalten mit vielen ähnlichen Mustern/Trends besteht, enthalten diese Datenspalten höchstwahrscheinlich identische Informationen. Außerdem können Dimensionen, die eine höhere Korrelation darstellen, die Leistung des Modells beeinträchtigen. In einem solchen Fall reicht eine dieser Variablen aus, um das ML-Modell zu füttern.

In solchen Situationen ist es am besten, die Pearson-Korrelationsmatrix zu verwenden, um die Variablen zu identifizieren, die eine hohe Korrelation aufweisen. Sobald sie identifiziert sind, können Sie eine davon mit VIF (Variance Inflation Factor) auswählen. Sie können alle Variablen mit einem höheren Wert ( VIF > 5 ) entfernen. Bei diesem Ansatz müssen Sie den Korrelationskoeffizienten zwischen numerischen Spalten ( Produkt-Moment-Koeffizient nach Pearson ) und zwischen nominalen Spalten ( Chi-Quadrat-Wert nach Pearson ) berechnen. Hier werden alle Spaltenpaare mit einem Korrelationskoeffizienten über dem eingestellten Schwellenwert auf 1 reduziert.

Da die Korrelation maßstabsabhängig ist, müssen Sie eine Spaltennormalisierung durchführen.

8. Beseitigung von Rückwärtsmerkmalen

Bei der Rückwärtsmerkmals-Eliminierungstechnik müssen Sie mit allen 'n'-Dimensionen beginnen. Somit können Sie bei einer bestimmten Iteration einen bestimmten Klassifizierungsalgorithmus trainieren, der auf n Eingabemerkmale trainiert wird. Jetzt müssen Sie jeweils ein Eingabemerkmal entfernen und dasselbe Modell n-mal mit n -1 Eingabevariablen trainieren . Dann entfernen Sie die Eingabevariable, deren Eliminierung den geringsten Anstieg der Fehlerrate erzeugt, wodurch n-1 Eingabemerkmale zurückbleiben. Außerdem wiederholen Sie die Klassifizierung mit n-2 Merkmalen, und dies wird fortgesetzt, bis keine andere Variable entfernt werden kann.

Jede Iteration ( k) erzeugt ein Modell, das auf nk Merkmale mit einer Fehlerrate von e(k) trainiert wurde . Anschließend müssen Sie die maximal erträgliche Fehlerrate auswählen, um die kleinste Anzahl von Merkmalen zu definieren, die erforderlich sind, um diese Klassifizierungsleistung mit dem gegebenen ML-Algorithmus zu erreichen.

Lesen Sie auch: Warum Datenanalyse im Geschäftsleben wichtig ist

9. Aufbau von Vorwärtsmerkmalen

Die Vorwärts-Feature-Konstruktion ist das Gegenteil des Rückwärts-Feature-Eliminierungs-Verfahrens. Bei der Vorwärts-Feature-Konstruktionsmethode beginnen Sie mit einem Feature und fahren fort, indem Sie ein Feature nach dem anderen hinzufügen (dies ist die Variable, die zu der größten Leistungssteigerung führt).

Sowohl die Vorwärtsmerkmalskonstruktion als auch die Rückwärtsmerkmalseliminierung sind zeit- und rechenintensiv. Diese Methoden eignen sich am besten für Datasets, die bereits über eine geringe Anzahl von Eingabespalten verfügen.

10. Zufällige Wälder

Random Forests sind nicht nur hervorragende Klassifikatoren, sondern auch äußerst nützlich für die Merkmalsauswahl. Bei diesem Dimensionsreduktionsansatz müssen Sie sorgfältig ein umfangreiches Netzwerk von Bäumen gegen ein Zielattribut konstruieren. Beispielsweise können Sie eine große Menge (z. B. 2000) flacher Bäume (z. B. mit zwei Ebenen) erstellen, wobei jeder Baum auf einem kleinen Bruchteil (3) der Gesamtzahl von Attributen trainiert wird.

Das Ziel besteht darin, die Nutzungsstatistiken jedes Attributs zu verwenden, um die informativste Teilmenge von Merkmalen zu identifizieren. Wird ein Attribut als bester Split gefunden, enthält es in der Regel ein informatives Merkmal, das es wert ist, berücksichtigt zu werden. Wenn Sie die Punktzahl der Nutzungsstatistiken eines Attributs in der zufälligen Gesamtstruktur im Verhältnis zu anderen Attributen berechnen, erhalten Sie die aussagekräftigsten Attribute.

Fazit

Zusammenfassend lässt sich sagen, dass keine Technik die absolut beste ist, wenn es um die Reduzierung der Dimensionalität geht. Jedes hat seine Macken und Vorteile. Der beste Weg, Techniken zur Dimensionsreduktion zu implementieren, besteht daher darin, systematische und kontrollierte Experimente durchzuführen, um herauszufinden, welche Technik(en) mit Ihrem Modell funktioniert und welche die beste Leistung für einen bestimmten Datensatz liefert.

Wenn Sie mehr über maschinelles Lernen erfahren möchten, sehen Sie sich das PG-Diplom in maschinellem Lernen und KI von IIIT-B & upGrad an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenge Schulungen, mehr als 30 Fallstudien und Aufgaben bietet, IIIT- B-Alumni-Status, mehr als 5 praktische, praktische Abschlussprojekte und Jobunterstützung bei Top-Unternehmen.