10 лучших методов уменьшения размерности для машинного обучения

Каждую секунду мир генерирует беспрецедентный объем данных. Поскольку данные стали важнейшим компонентом предприятий и организаций во всех отраслях, важно правильно обрабатывать, анализировать и визуализировать их, чтобы извлекать ценную информацию из больших наборов данных. Однако есть одна загвоздка – больше не всегда означает продуктивность и точность. Чем больше данных мы производим каждую секунду, тем сложнее их анализировать и визуализировать, чтобы делать правильные выводы.

Здесь в игру вступает уменьшение размерности .

Что такое уменьшение размерности?

Проще говоря, уменьшение размерности относится к методу уменьшения размерности набора признаков данных. Обычно наборы данных машинного обучения (набор признаков) содержат сотни столбцов (то есть признаков) или массив точек, создавая массивную сферу в трехмерном пространстве. Применяя уменьшение размерности , вы можете уменьшить или довести количество столбцов до поддающихся количественному измерению значений, тем самым превратив трехмерную сферу в двумерный объект (круг).

Теперь возникает вопрос, почему вы должны сокращать количество столбцов в наборе данных, если вы можете напрямую передать его алгоритму машинного обучения и позволить ему все обработать самостоятельно?

Проклятие размерности требует применения уменьшения размерности .

Проклятие размерности

Проклятие размерности — это явление, которое возникает, когда вы работаете (анализируете и визуализируете) с данными в многомерных пространствах, которых нет в низкоразмерных пространствах.

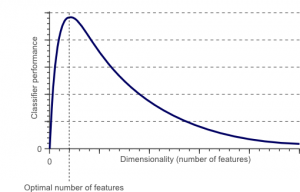
Источник

Чем больше число признаков или факторов (иначе переменных) в наборе признаков, тем сложнее визуализировать обучающий набор и работать с ним. Еще один важный момент, который следует учитывать, заключается в том, что большинство переменных часто коррелируют. Таким образом, если вы продумаете каждую переменную в наборе признаков, вы включите в обучающий набор множество избыточных факторов.

Кроме того, чем больше у вас переменных, тем больше будет количество выборок для представления всех возможных комбинаций значений признаков в примере. Когда количество переменных увеличивается, модель становится более сложной, что увеличивает вероятность переобучения. Когда вы обучаете модель машинного обучения на большом наборе данных, содержащем множество функций, она обязательно будет зависеть от обучающих данных. Это приведет к тому, что переобученная модель не сможет хорошо работать с реальными данными.

Основная цель уменьшения размерности — избежать переобучения. Данные для обучения со значительно меньшим количеством функций гарантируют, что ваша модель останется простой — она будет делать меньшие предположения.

Помимо этого, уменьшение размерности имеет много других преимуществ, таких как:

• Это устраняет шум и избыточные функции.
• Это помогает повысить точность и производительность модели.
• Это облегчает использование алгоритмов, непригодных для более существенных измерений.
• Это уменьшает объем требуемого места для хранения (чем меньше данных, тем меньше места для хранения).
• Он сжимает данные, что сокращает время вычислений и способствует более быстрому обучению данных.

Читайте : Что такое линейный дискриминантный анализ

Методы уменьшения размерности

Методы уменьшения размерности можно разделить на две большие категории:

1. Выбор функции

Метод выбора признаков направлен на поиск подмножества входных переменных (наиболее релевантных) из исходного набора данных. Выбор признаков включает в себя три стратегии, а именно:

• Стратегия фильтрации
• Стратегия обертки
• Встроенная стратегия

2. Извлечение признаков

Извлечение признаков, также известное как проекция признаков, преобразует данные из многомерного пространства в пространство с меньшими размерами. Это преобразование данных может быть как линейным, так и нелинейным. Этот метод находит меньший набор новых переменных, каждая из которых представляет собой комбинацию входных переменных (содержащих ту же информацию, что и входные переменные).

Без дальнейших церемоний, давайте углубимся в подробное обсуждение нескольких часто используемых методов уменьшения размерности!

1. Анализ основных компонентов (PCA)

Анализ главных компонентов является одним из ведущих линейных методов уменьшения размерности. Этот метод выполняет прямое сопоставление данных с пространством меньшей размерности таким образом, чтобы максимизировать дисперсию данных в низкоразмерном представлении.

По сути, это статистическая процедура, которая ортогонально преобразует « n» координат набора данных в новый набор из n координат, известных как главные компоненты. Это преобразование приводит к созданию первой главной компоненты, имеющей максимальную дисперсию. Каждый последующий главный компонент имеет максимально возможную дисперсию при условии, что он ортогонален (не коррелирован) с предыдущими компонентами.

Преобразование PCA чувствительно к относительному масштабированию исходных переменных. Таким образом, диапазоны столбцов данных должны быть сначала нормализованы перед внедрением метода PCA. Еще одна вещь, которую следует помнить, заключается в том, что использование подхода PCA приведет к тому, что ваш набор данных потеряет интерпретируемость. Таким образом, если интерпретируемость имеет решающее значение для вашего анализа, PCA не является правильным методом уменьшения размерности для вашего проекта.

2. Неотрицательная матричная факторизация (NMF)

NMF разбивает неотрицательную матрицу на произведение двух неотрицательных. Именно это делает метод NMF ценным инструментом в областях, которые в первую очередь связаны с неотрицательными сигналами (например, в астрономии). Правило мультипликативного обновления, разработанное Lee & Seung, улучшило метод NMF за счет включения неопределенностей, учета отсутствующих данных и параллельных вычислений, а также последовательного построения.

Эти включения помогли сделать подход NMF стабильным и линейным. В отличие от PCA, NMF не устраняет среднее значение матриц, тем самым создавая нефизические неотрицательные потоки. Таким образом, NMF может сохранить больше информации, чем метод PCA.

Последовательный НМП характеризуется стабильной компонентной базой при строительстве и линейным процессом моделирования. Это делает его идеальным инструментом в астрономии. Последовательный NMF может сохранить поток при прямом отображении околозвездных структур в астрономии, например, при обнаружении экзопланет и прямом отображении околозвездных дисков.

3. Линейный дискриминантный анализ (ЛДА)

Линейный дискриминантный анализ является обобщением линейного дискриминантного метода Фишера, который широко применяется в статистике, распознавании образов и машинном обучении. Техника LDA направлена ​​​​на поиск линейной комбинации признаков, которые могут характеризовать или различать два или более классов объектов. LDA представляет данные таким образом, чтобы максимизировать разделимость классов. В то время как объекты, принадлежащие к одному и тому же классу, сопоставляются посредством проекции, объекты из разных классов располагаются далеко друг от друга.

4. Обобщенный дискриминантный анализ (GDA)

Обобщенный дискриминантный анализ — это нелинейный дискриминантный анализ, использующий оператор функции ядра. Его лежащая в основе теория очень близко соответствует теории машин опорных векторов (SVM), так что метод GDA помогает отображать входные векторы в многомерное пространство признаков. Подобно подходу LDA, GDA также стремится найти проекцию переменных в пространстве меньшей размерности, максимизируя отношение разброса между классами к разбросу внутри класса.

5. Соотношение пропущенных значений

При изучении данного набора данных вы можете обнаружить, что в наборе данных отсутствуют некоторые значения. Первым шагом в работе с пропущенными значениями является определение их причины. Соответственно, вы можете вписать пропущенные значения или вообще отбросить их, используя подходящие методы. Этот подход идеально подходит для ситуаций, когда есть несколько пропущенных значений.

Однако что делать, если пропущено слишком много значений, скажем, более 50%? В таких ситуациях можно установить пороговое значение и использовать метод соотношения пропущенных значений. Чем выше пороговое значение, тем агрессивнее будет уменьшение размерности. Если процент отсутствующих значений в переменной превышает пороговое значение, вы можете удалить эту переменную.

Как правило, столбцы данных с многочисленными пропущенными значениями вряд ли содержат полезную информацию. Таким образом, вы можете удалить все столбцы данных, в которых пропущенные значения превышают установленный порог.

6. Фильтр низкой дисперсии

Точно так же, как вы используете метод соотношения пропущенных значений для пропущенных переменных, так и для постоянных переменных существует метод фильтра с низкой дисперсией. Когда в наборе данных есть постоянные переменные, невозможно улучшить производительность модели. Почему? Потому что он имеет нулевую дисперсию.

В этом методе также можно установить пороговое значение для исключения всех постоянных переменных. Таким образом, все столбцы данных с дисперсией ниже порогового значения будут исключены. Тем не менее, одна вещь, которую вы должны помнить о методе фильтра с низкой дисперсией, заключается в том, что дисперсия зависит от диапазона. Таким образом, перед реализацией этого метода уменьшения размерности необходима нормализация.

7. Высококорреляционный фильтр

Если набор данных состоит из столбцов данных, имеющих много схожих шаблонов/тенденций, эти столбцы данных, скорее всего, будут содержать идентичную информацию. Кроме того, измерения, отображающие более высокую корреляцию, могут отрицательно сказаться на производительности модели. В таком случае одной из этих переменных достаточно для подачи модели ML.

В таких ситуациях лучше всего использовать корреляционную матрицу Пирсона, чтобы определить переменные, демонстрирующие высокую корреляцию. Как только они определены, вы можете выбрать один из них, используя VIF (коэффициент инфляции дисперсии). Вы можете удалить все переменные, имеющие более высокое значение (VIF > 5). В этом подходе вы должны рассчитать коэффициент корреляции между числовыми столбцами ( коэффициент момента продукта Пирсона ) и между номинальными столбцами ( значение хи-квадрат Пирсона ). Здесь все пары столбцов, имеющие коэффициент корреляции выше установленного порога, будут уменьшены до 1.

Поскольку корреляция чувствительна к масштабу, необходимо выполнить нормализацию столбцов.

8. Устранение обратных функций

В методе устранения обратных признаков вы должны начать со всех «n» измерений. Таким образом, на заданной итерации можно обучить конкретный алгоритм классификации на n входных признаках. Теперь вам нужно удалять по одной входной функции за раз и обучать одну и ту же модель на n-1 входных переменных n раз. Затем вы удаляете входную переменную, устранение которой приводит к наименьшему увеличению частоты ошибок, что оставляет после себя n-1 входных признаков. Далее вы повторяете классификацию с использованием n-2 признаков, и так продолжается до тех пор, пока никакая другая переменная не может быть удалена.

Каждая итерация ( k ) создает модель, обученную на nk функциях, с частотой ошибок e(k) . После этого вы должны выбрать максимально допустимую частоту ошибок, чтобы определить наименьшее количество функций, необходимых для достижения этой производительности классификации с данным алгоритмом ML.

Читайте также: Почему анализ данных важен в бизнесе

9. Построение прямой функции

Построение прямого признака противоположно методу исключения обратного признака. В методе прямого построения признаков вы начинаете с одного признака и продолжаете добавлять по одному признаку за раз (это переменная, которая приводит к наибольшему повышению производительности).

Как прямое построение признаков, так и устранение обратных признаков требуют много времени и больших вычислительных ресурсов. Эти методы лучше всего подходят для наборов данных с небольшим количеством входных столбцов.

10. Случайные леса

Случайные леса являются не только отличными классификаторами, но и чрезвычайно полезными для выбора признаков. При таком подходе к уменьшению размерности вы должны тщательно построить разветвленную сеть деревьев по целевому атрибуту. Например, вы можете создать большой набор (скажем, 2000) неглубоких деревьев (скажем, с двумя уровнями), где каждое дерево обучается на меньшей доле (3) от общего числа атрибутов.

Цель состоит в том, чтобы использовать статистику использования каждого атрибута, чтобы определить наиболее информативное подмножество функций. Если атрибут считается лучшим разделением, он обычно содержит информативную функцию, заслуживающую внимания. Когда вы вычисляете оценку статистики использования атрибута в случайном лесу по отношению к другим атрибутам, вы получаете наиболее предсказуемые атрибуты.

Заключение

В заключение, когда дело доходит до уменьшения размерности, ни один метод не является абсолютно лучшим. У каждого есть свои особенности и преимущества. Таким образом, лучший способ реализовать методы уменьшения размерности — это использовать систематические и контролируемые эксперименты, чтобы выяснить, какие методы работают с вашей моделью и какие обеспечивают наилучшую производительность в данном наборе данных.

Если вам интересно узнать больше о машинном обучении, ознакомьтесь с дипломом PG IIIT-B и upGrad в области машинного обучения и искусственного интеллекта, который предназначен для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 тематических исследований и заданий, IIIT- Статус B Alumni, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.