Las 10 mejores técnicas de reducción de dimensionalidad para el aprendizaje automático

Cada segundo, el mundo genera un volumen de datos sin precedentes. Dado que los datos se han convertido en un componente crucial de las empresas y organizaciones en todas las industrias, es esencial procesarlos, analizarlos y visualizarlos adecuadamente para extraer información significativa de grandes conjuntos de datos. Sin embargo, hay una trampa: más no siempre significa productivo y preciso. Cuantos más datos producimos cada segundo, más difícil es analizarlos y visualizarlos para sacar inferencias válidas.

Aquí es donde entra en juego la reducción de la dimensionalidad .

¿Qué es la Reducción de Dimensionalidad?

En palabras simples, la reducción de la dimensionalidad se refiere a la técnica de reducir la dimensión de un conjunto de características de datos. Por lo general, los conjuntos de datos de aprendizaje automático (conjunto de características) contienen cientos de columnas (es decir, características) o una matriz de puntos, lo que crea una esfera masiva en un espacio tridimensional. Al aplicar la reducción de dimensionalidad , puede disminuir o reducir el número de columnas a recuentos cuantificables, transformando así la esfera tridimensional en un objeto bidimensional (círculo).

Ahora viene la pregunta, ¿por qué debe reducir las columnas en un conjunto de datos cuando puede introducirlo directamente en un algoritmo ML y dejar que resuelva todo por sí mismo?

La maldición de la dimensionalidad exige la aplicación de la reducción de la dimensionalidad .

La maldición de la dimensionalidad

La maldición de la dimensionalidad es un fenómeno que surge cuando trabajas (analizas y visualizas) con datos en espacios de alta dimensión que no existen en espacios de baja dimensión.

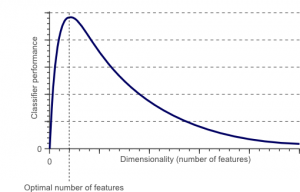
Fuente

Cuanto mayor sea el número de características o factores (también conocido como variables) en un conjunto de características, más difícil será visualizar el conjunto de entrenamiento y trabajar en él. Otro punto vital a considerar es que la mayoría de las variables a menudo están correlacionadas. Entonces, si piensa en cada variable dentro del conjunto de características, incluirá muchos factores redundantes en el conjunto de entrenamiento.

Además, cuantas más variables tenga a mano, mayor será el número de muestras para representar todas las combinaciones posibles de valores de características en el ejemplo. Cuando aumenta el número de variables, el modelo se vuelve más complejo, lo que aumenta la probabilidad de sobreajuste. Cuando entrena un modelo de ML en un gran conjunto de datos que contiene muchas características, seguramente dependerá de los datos de entrenamiento. Esto dará como resultado un modelo sobreajustado que no funciona bien en datos reales.

El objetivo principal de la reducción de la dimensionalidad es evitar el sobreajuste. Los datos de entrenamiento con características considerablemente menores garantizarán que su modelo siga siendo simple: hará suposiciones más pequeñas.

Aparte de esto, la reducción de la dimensionalidad tiene muchos otros beneficios, tales como:

• Elimina el ruido y las características redundantes.
• Ayuda a mejorar la precisión y el rendimiento del modelo.
• Facilita el uso de algoritmos que no son aptos para dimensiones más sustanciales.
• Reduce la cantidad de espacio de almacenamiento requerido (menos datos necesitan menos espacio de almacenamiento).
• Comprime los datos, lo que reduce el tiempo de cálculo y facilita un entrenamiento más rápido de los datos.

Leer: ¿Qué es el análisis discriminante lineal?

Técnicas de reducción de dimensionalidad

Las técnicas de reducción de la dimensionalidad se pueden clasificar en dos grandes categorías:

1. Selección de características

El método de selección de características tiene como objetivo encontrar un subconjunto de las variables de entrada (que son las más relevantes) del conjunto de datos original. La selección de características incluye tres estrategias, a saber:

• Filtrar estrategia
• Estrategia de envoltura
• estrategia integrada

2. Extracción de características

La extracción de características, también conocida como proyección de características, convierte los datos del espacio de alta dimensión a uno con dimensiones menores. Esta transformación de datos puede ser lineal o también puede ser no lineal. Esta técnica encuentra un conjunto más pequeño de nuevas variables, cada una de las cuales es una combinación de variables de entrada (que contienen la misma información que las variables de entrada).

¡Sin más preámbulos, profundicemos en una discusión detallada de algunas técnicas de reducción de dimensionalidad comúnmente utilizadas!

1. Análisis de componentes principales (PCA)

El análisis de componentes principales es una de las principales técnicas lineales de reducción de dimensionalidad. Este método realiza una asignación directa de los datos a un espacio dimensional menor de una manera que maximiza la varianza de los datos en la representación de dimensiones bajas.

Esencialmente, es un procedimiento estadístico que convierte ortogonalmente las coordenadas ' n' de un conjunto de datos en un nuevo conjunto de n coordenadas, conocidas como componentes principales. Esta conversión da como resultado la creación del primer componente principal que tiene la varianza máxima. Cada componente principal subsiguiente tiene la varianza más alta posible, con la condición de que sea ortogonal (no correlacionado) con los componentes anteriores.

La conversión de PCA es sensible a la escala relativa de las variables originales. Por lo tanto, los rangos de las columnas de datos primero deben normalizarse antes de implementar el método PCA. Otra cosa para recordar es que usar el enfoque PCA hará que su conjunto de datos pierda su interpretabilidad. Entonces, si la interpretabilidad es crucial para su análisis, PCA no es el método de reducción de dimensionalidad adecuado para su proyecto.

2. Factorización matricial no negativa (NMF)

NMF descompone una matriz no negativa en el producto de dos no negativas. Esto es lo que hace que el método NMF sea una herramienta valiosa en áreas que se ocupan principalmente de señales no negativas (por ejemplo, astronomía). La regla de actualización multiplicativa de Lee & Seung mejoró la técnica NMF al incluir incertidumbres, considerar los datos faltantes y el cálculo paralelo y la construcción secuencial.

Estas inclusiones contribuyeron a que el enfoque NMF fuera estable y lineal. A diferencia de PCA, NMF no elimina la media de las matrices, por lo que crea flujos no físicos no negativos. Por lo tanto, NMF puede conservar más información que el método PCA.

NMF secuencial se caracteriza por una base de componentes estable durante la construcción y un proceso de modelado lineal. Esto lo convierte en la herramienta perfecta en astronomía. La NMF secuencial puede preservar el flujo en la obtención de imágenes directas de estructuras circunestelares en astronomía, como la detección de exoplanetas y la obtención de imágenes directas de discos circunestelares.

3. Análisis discriminante lineal (LDA)

El análisis discriminante lineal es una generalización del método discriminante lineal de Fisher que se aplica ampliamente en estadística, reconocimiento de patrones y aprendizaje automático. La técnica LDA tiene como objetivo encontrar una combinación lineal de características que puedan caracterizar o diferenciar entre dos o más clases de objetos. LDA representa los datos de una manera que maximiza la separabilidad de clases. Mientras que los objetos que pertenecen a la misma clase se yuxtaponen a través de la proyección, los objetos de diferentes clases se organizan muy separados.

4. Análisis discriminante generalizado (GDA)

El análisis discriminante generalizado es un análisis discriminante no lineal que aprovecha el operador de función kernel. Su teoría subyacente coincide muy de cerca con la de las máquinas de vectores de soporte (SVM), de modo que la técnica GDA ayuda a mapear los vectores de entrada en un espacio de características de alta dimensión. Al igual que el enfoque LDA, GDA también busca encontrar una proyección para las variables en un espacio de menor dimensión maximizando la relación entre las dispersiones entre clases y la dispersión dentro de las clases.

5. Relación de valores faltantes

Cuando explore un conjunto de datos determinado, es posible que descubra que faltan algunos valores en el conjunto de datos. El primer paso para lidiar con los valores faltantes es identificar la razón detrás de ellos. En consecuencia, puede imputar los valores faltantes o eliminarlos por completo utilizando los métodos adecuados. Este enfoque es perfecto para situaciones en las que faltan algunos valores.

Sin embargo, ¿qué hacer cuando faltan demasiados valores, por ejemplo, más del 50 %? En tales situaciones, puede establecer un valor de umbral y utilizar el método de proporción de valores faltantes. Cuanto mayor sea el valor del umbral, más agresiva será la reducción de la dimensionalidad. Si el porcentaje de valores faltantes en una variable supera el umbral, puede descartar la variable.

Generalmente, las columnas de datos que tienen numerosos valores faltantes apenas contienen información útil. Por lo tanto, puede eliminar todas las columnas de datos que tengan valores faltantes superiores al umbral establecido.

6. Filtro de baja varianza

Así como usa el método de proporción de valores faltantes para variables faltantes, para variables constantes, existe la técnica de filtro de baja varianza. Cuando un conjunto de datos tiene variables constantes, no es posible mejorar el rendimiento del modelo. ¿Por qué? Porque tiene varianza cero.

En este método también, puede establecer un valor de umbral para eliminar todas las variables constantes. Por lo tanto, se eliminarán todas las columnas de datos con una varianza inferior al valor umbral. Sin embargo, una cosa que debe recordar sobre el método de filtro de baja varianza es que la varianza depende del rango. Por lo tanto, la normalización es imprescindible antes de implementar esta técnica de reducción de dimensionalidad.

7. Filtro de alta correlación

Si un conjunto de datos consta de columnas de datos que tienen muchos patrones/tendencias similares, es muy probable que estas columnas de datos contengan información idéntica. Además, las dimensiones que representan una correlación más alta pueden afectar negativamente el rendimiento del modelo. En tal caso, una de esas variables es suficiente para alimentar el modelo ML.

Para tales situaciones, es mejor usar la matriz de correlación de Pearson para identificar las variables que muestran una correlación alta. Una vez identificados, puede seleccionar uno de ellos usando VIF (Variance Inflation Factor). Puede eliminar todas las variables que tengan un valor más alto ( VIF > 5 ). En este enfoque, debe calcular el coeficiente de correlación entre columnas numéricas ( Coeficiente de momento del producto de Pearson ) y entre columnas nominales ( Valor de chi-cuadrado de Pearson ). Aquí, todos los pares de columnas que tengan un coeficiente de correlación superior al umbral establecido se reducirán a 1.

Dado que la correlación es sensible a la escala, debe realizar la normalización de columnas.

8. Eliminación de funciones hacia atrás

En la técnica de eliminación de características hacia atrás, debe comenzar con todas las dimensiones 'n'. Por lo tanto, en una iteración dada, puede entrenar un algoritmo de clasificación específico en n características de entrada. Ahora, debe eliminar una característica de entrada a la vez y entrenar el mismo modelo en n-1 variables de entrada n veces. Luego elimina la variable de entrada cuya eliminación genera el menor aumento en la tasa de error, lo que deja n-1 características de entrada. Además, repite la clasificación usando n-2 características, y esto continúa hasta que no se puede eliminar ninguna otra variable.

Cada iteración ( k) crea un modelo entrenado en nk características que tienen una tasa de error de e(k) . Después de esto, debe seleccionar la tasa de error máxima tolerable para definir la menor cantidad de características necesarias para alcanzar ese rendimiento de clasificación con el algoritmo ML dado.

Lea también: Por qué el análisis de datos es importante en los negocios

9. Construcción de funciones de avance

La construcción de características hacia adelante es lo opuesto al método de eliminación de características hacia atrás. En el método de construcción directa de funciones, comienza con una función y continúa progresando agregando una función a la vez (esta es la variable que da como resultado el mayor impulso en el rendimiento).

Tanto la construcción de características hacia adelante como la eliminación de características hacia atrás requieren mucho tiempo y computación. Estos métodos son más adecuados para conjuntos de datos que ya tienen un número bajo de columnas de entrada.

10. Bosques aleatorios

Los bosques aleatorios no solo son excelentes clasificadores, sino que también son extremadamente útiles para la selección de características. En este enfoque de reducción de dimensionalidad, debe construir cuidadosamente una red extensa de árboles contra un atributo de destino. Por ejemplo, puede crear un conjunto grande (digamos, 2000) de árboles poco profundos (digamos, que tengan dos niveles), donde cada árbol se entrena en una fracción menor (3) del número total de atributos.

El objetivo es utilizar las estadísticas de uso de cada atributo para identificar el subconjunto de funciones más informativo. Si se encuentra que un atributo es la mejor división, generalmente contiene una característica informativa que vale la pena considerar. Cuando calcula la puntuación de las estadísticas de uso de un atributo en el bosque aleatorio en relación con otros atributos, obtiene los atributos más predictivos.

Conclusión

Para concluir, cuando se trata de reducción de dimensionalidad, ninguna técnica es la mejor. Cada uno tiene sus peculiaridades y ventajas. Por lo tanto, la mejor manera de implementar técnicas de reducción de dimensionalidad es usar experimentos sistemáticos y controlados para descubrir qué técnica(s) funciona(n) con su modelo y cuál ofrece el mejor rendimiento en un conjunto de datos determinado.

Si está interesado en obtener más información sobre el aprendizaje automático, consulte el Diploma PG en aprendizaje automático e IA de IIIT-B y upGrad, que está diseñado para profesionales que trabajan y ofrece más de 450 horas de capacitación rigurosa, más de 30 estudios de casos y asignaciones, IIIT- B Estado de exalumno, más de 5 proyectos prácticos finales prácticos y asistencia laboral con las mejores empresas.