เทคนิคการลดมิติข้อมูล 10 อันดับแรกสำหรับการเรียนรู้ของเครื่อง

ทุกวินาที โลกสร้างปริมาณข้อมูลอย่างไม่เคยปรากฏมาก่อน เนื่องจากข้อมูลได้กลายเป็นองค์ประกอบสำคัญของธุรกิจและองค์กรในทุกอุตสาหกรรม จึงจำเป็นต้องประมวลผล วิเคราะห์ และแสดงภาพอย่างเหมาะสมเพื่อดึงข้อมูลเชิงลึกที่มีความหมายจากชุดข้อมูลขนาดใหญ่ อย่างไรก็ตาม มีสิ่งที่จับได้ – มากกว่านั้นไม่ได้หมายความว่ามีประสิทธิผลและแม่นยำเสมอไป ยิ่งเราสร้างข้อมูลทุก ๆ วินาทีมากเท่าไหร่ ก็ยิ่งท้าทายมากขึ้นในการวิเคราะห์และแสดงภาพข้อมูลเพื่อทำการอนุมานที่ถูกต้อง

นี่คือจุดเริ่มต้นของ การลดมิติข้อมูล

การลดมิติคืออะไร?

พูดง่ายๆ ก็คือ การลดขนาด หมายถึงเทคนิคในการลดขนาดของชุดคุณลักษณะข้อมูล โดยปกติ ชุดข้อมูลการเรียนรู้ของเครื่อง (ชุดคุณลักษณะ) ประกอบด้วยคอลัมน์นับร้อย (เช่น คุณลักษณะ) หรืออาร์เรย์ของจุด ทำให้เกิดทรงกลมขนาดใหญ่ในพื้นที่สามมิติ เมื่อใช้การ ลดมิติข้อมูล คุณจะลดหรือลดจำนวนคอลัมน์ลงเป็นจำนวนที่วัดได้ ดังนั้นจะเปลี่ยนทรงกลมสามมิติเป็นวัตถุสองมิติ (วงกลม)

มาถึงคำถามแล้ว ทำไมคุณต้องลดคอลัมน์ในชุดข้อมูลในเมื่อคุณสามารถป้อนลงในอัลกอริธึม ML ได้โดยตรงและปล่อยให้มันทำงานทุกอย่างด้วยตัวเอง

คำสาปของมิติกำหนดการประยุกต์ใช้ การลดมิติ

คำสาปแห่งมิติ

คำสาปของมิติเป็นปรากฏการณ์ที่เกิดขึ้นเมื่อคุณทำงาน (วิเคราะห์และเห็นภาพ) กับข้อมูลในพื้นที่มิติสูงที่ไม่มีอยู่ในช่องว่างมิติต่ำ

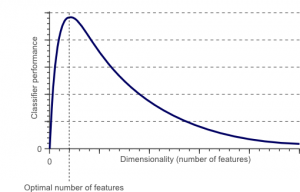
แหล่งที่มา

ยิ่งจำนวนคุณลักษณะหรือปัจจัย (ตัวแปรที่เรียกว่า) ในชุดคุณลักษณะยิ่งสูง ยิ่งทำให้เห็นภาพชุดการฝึกและดำเนินการได้ยากขึ้น จุดสำคัญอีกประการที่ต้องพิจารณาคือตัวแปรส่วนใหญ่มักมีความสัมพันธ์กัน ดังนั้น หากคุณคิดว่าทุกตัวแปรภายในชุดคุณลักษณะ คุณจะต้องรวมปัจจัยที่ซ้ำซ้อนจำนวนมากในชุดการฝึก

นอกจากนี้ ยิ่งคุณมีตัวแปรมากเท่าใด จำนวนของตัวอย่างก็จะยิ่งสูงขึ้นเท่านั้น เพื่อแสดงชุดค่าผสมที่เป็นไปได้ของค่าคุณลักษณะในตัวอย่าง เมื่อจำนวนตัวแปรเพิ่มขึ้น แบบจำลองจะซับซ้อนมากขึ้น ซึ่งจะเป็นการเพิ่มโอกาสในการปรับให้เหมาะสม เมื่อคุณฝึกโมเดล ML บนชุดข้อมูลขนาดใหญ่ที่มีคุณลักษณะมากมาย มันจะต้องขึ้นอยู่กับข้อมูลการฝึก ซึ่งจะส่งผลให้มีรูปแบบที่มากเกินไปซึ่งไม่สามารถทำงานได้ดีกับข้อมูลจริง

เป้าหมายหลักของการลดขนาดคือการหลีกเลี่ยงการใส่มากเกินไป ข้อมูลการฝึกที่มีคุณสมบัติน้อยกว่ามากจะช่วยให้มั่นใจได้ว่าแบบจำลองของคุณยังคงเรียบง่าย - จะทำให้สมมติฐานเล็กลง

นอกจากนี้ การลดขนาดยังมีประโยชน์อื่นๆ อีกมากมาย เช่น:

• มันกำจัดเสียงรบกวนและคุณสมบัติที่ซ้ำซ้อน
• ช่วยปรับปรุงความแม่นยำและประสิทธิภาพของโมเดล
• อำนวยความสะดวกในการใช้อัลกอริธึมที่ไม่เหมาะสมกับมิติที่ใหญ่กว่า
• ช่วยลดปริมาณพื้นที่จัดเก็บที่ต้องการ (ข้อมูลน้อยต้องการพื้นที่จัดเก็บน้อยลง)
• มันบีบอัดข้อมูลซึ่งช่วยลดเวลาในการคำนวณและอำนวยความสะดวกในการฝึกอบรมข้อมูลได้เร็วขึ้น

อ่าน : L inear discriminant analysis คืออะไร

เทคนิคการลดมิติ

เทคนิคการลดขนาดมิติสามารถแบ่งออกเป็นสองประเภทกว้าง ๆ :

1. การเลือกคุณสมบัติ

วิธีการเลือกคุณสมบัติมีจุดมุ่งหมายเพื่อค้นหาชุดย่อยของตัวแปรอินพุต (ที่เกี่ยวข้องมากที่สุด) จากชุดข้อมูลดั้งเดิม การเลือกคุณสมบัติประกอบด้วยสามกลยุทธ์ กล่าวคือ:

• กลยุทธ์การกรอง
• กลยุทธ์กระดาษห่อ
• กลยุทธ์ที่ฝังตัว

2. การแยกคุณลักษณะ

การแยกคุณลักษณะ หรือที่เรียกว่า การฉายคุณลักษณะ จะแปลงข้อมูลจากพื้นที่มิติสูงเป็นพื้นที่ที่มีมิติน้อยกว่า การแปลงข้อมูลนี้อาจเป็นแบบเชิงเส้นหรือแบบไม่เป็นเชิงเส้นก็ได้เช่นกัน เทคนิคนี้จะค้นหาชุดตัวแปรใหม่ที่มีขนาดเล็กลง โดยแต่ละชุดประกอบด้วยตัวแปรอินพุต (มีข้อมูลเดียวกันกับตัวแปรอินพุต)

โดยไม่ต้องกังวลใจอีกต่อไป มาดำดิ่งในการอภิปรายโดยละเอียดเกี่ยวกับเทคนิคการลดขนาดมิติที่ใช้กันทั่วไปสองสามข้อ!

1. การวิเคราะห์องค์ประกอบหลัก (PCA)

การวิเคราะห์องค์ประกอบหลักเป็นหนึ่งในเทคนิคเชิงเส้นตรงชั้นนำของการลดขนาด วิธีนี้จะทำการแมปข้อมูลโดยตรงไปยังพื้นที่มิติที่น้อยกว่าในลักษณะที่เพิ่มความแปรปรวนของข้อมูลสูงสุดในการแสดงมิติต่ำ

โดยพื้นฐานแล้ว มันคือขั้นตอนทางสถิติที่แปลง พิกัด ' n' ของชุดข้อมูลตามมุมฉากให้เป็นชุดใหม่ของ พิกัด n ซึ่งรู้จักกันในชื่อองค์ประกอบหลัก การแปลงนี้ส่งผลให้เกิดการสร้างองค์ประกอบหลักแรกที่มีความแปรปรวนสูงสุด องค์ประกอบหลักที่ตามมาแต่ละส่วนจะมีความแปรปรวนสูงสุดที่เป็นไปได้ ภายใต้เงื่อนไขว่าองค์ประกอบดังกล่าวเป็นมุมฉาก (ไม่สัมพันธ์กัน) กับส่วนประกอบก่อนหน้า

การแปลง PCA มีความอ่อนไหวต่อการปรับขนาดสัมพัทธ์ของตัวแปรดั้งเดิม ดังนั้น ช่วงของคอลัมน์ข้อมูลจะต้องถูกทำให้เป็นมาตรฐานก่อนจึงจะใช้วิธี PCA อีกสิ่งหนึ่งที่ต้องจำไว้คือการใช้แนวทาง PCA จะทำให้ชุดข้อมูลของคุณสูญเสียความสามารถในการตีความ ดังนั้น หากความสามารถในการตีความมีความสำคัญต่อการวิเคราะห์ของคุณ PCA ไม่ใช่วิธีการลดขนาดที่เหมาะสมสำหรับโครงการของคุณ

2. การแยกตัวประกอบเมทริกซ์ที่ไม่เป็นลบ (NMF)

NMF แบ่งเมทริกซ์ที่ไม่เป็นลบออกเป็นผลคูณของเมทริกซ์ที่ไม่เป็นลบสองตัว นี่คือสิ่งที่ทำให้วิธี NMF เป็นเครื่องมือที่มีค่าในพื้นที่ที่เกี่ยวข้องกับสัญญาณที่ไม่เป็นลบเป็นหลัก (เช่น ดาราศาสตร์) กฎการอัปเดตการคูณโดย Lee & Seung ได้ปรับปรุงเทคนิค NMF โดยรวมถึงความไม่แน่นอน พิจารณาข้อมูลที่ขาดหายไปและการคำนวณแบบคู่ขนาน และการสร้างตามลำดับ

การรวมเหล่านี้มีส่วนทำให้แนวทาง NMF มีเสถียรภาพและเป็นเส้นตรง NMF ไม่ได้กำจัดค่าเฉลี่ยของเมทริกซ์ต่างจาก PCA ดังนั้นจึงสร้างฟลักซ์ที่ไม่เป็นลบที่ไม่เป็นไปตามหลักฟิสิกส์ ดังนั้น NMF สามารถเก็บข้อมูลได้มากกว่าวิธี PCA

Sequential NMF มีลักษณะเฉพาะด้วยฐานส่วนประกอบที่มั่นคงระหว่างการก่อสร้างและกระบวนการสร้างแบบจำลองเชิงเส้น ทำให้เป็นเครื่องมือที่สมบูรณ์แบบในด้านดาราศาสตร์ NMF ตามลำดับสามารถรักษาฟลักซ์ในการถ่ายภาพโดยตรงของโครงสร้างรอบดาวในทางดาราศาสตร์ เช่น การตรวจจับดาวเคราะห์นอกระบบและการถ่ายภาพโดยตรงของดิสก์รอบดาว

3. การวิเคราะห์จำแนกเชิงเส้น (LDA)

การวิเคราะห์จำแนกเชิงเส้นเป็นลักษณะทั่วไปของวิธีการจำแนกเชิงเส้นของฟิชเชอร์ที่ใช้กันอย่างแพร่หลายในด้านสถิติ การรู้จำรูปแบบ และการเรียนรู้ของเครื่อง เทคนิค LDA มีจุดมุ่งหมายเพื่อค้นหาการผสมผสานเชิงเส้นของคุณลักษณะที่สามารถกำหนดลักษณะหรือแยกความแตกต่างระหว่างวัตถุสองประเภทขึ้นไป LDA แสดงถึงข้อมูลในลักษณะที่เพิ่มความสามารถในการแยกชั้น ในขณะที่วัตถุที่อยู่ในคลาสเดียวกันนั้นถูกวางเรียงกันผ่านการฉายภาพ วัตถุจากคลาสที่ต่างกันจะถูกจัดเรียงแยกจากกัน

4. การวิเคราะห์การเลือกปฏิบัติทั่วไป (GDA)

การวิเคราะห์จำแนกทั่วไปเป็นการวิเคราะห์จำแนกแบบไม่เชิงเส้นที่ใช้ประโยชน์จากตัวดำเนินการฟังก์ชันเคอร์เนล ทฤษฎีที่เป็นพื้นฐานของมันมีความสอดคล้องอย่างใกล้ชิดกับเวกเตอร์เครื่องสนับสนุน (SVM) ซึ่งเทคนิค GDA จะช่วยแมปเวกเตอร์อินพุตในพื้นที่คุณลักษณะที่มีมิติสูง เช่นเดียวกับแนวทางของ LDA GDA ยังพยายามค้นหาการฉายภาพสำหรับตัวแปรในพื้นที่มิติที่ต่ำกว่าด้วยการเพิ่มอัตราส่วนของ scatters ระหว่างคลาสกับการ scatter ภายในคลาส

5. อัตราส่วนค่าที่ขาดหายไป

เมื่อคุณสำรวจชุดข้อมูลที่กำหนด คุณอาจพบว่ามีค่าบางอย่างที่ขาดหายไปในชุดข้อมูล ขั้นตอนแรกในการจัดการกับค่าที่หายไปคือการระบุเหตุผลเบื้องหลัง ดังนั้น คุณสามารถใส่ค่าที่หายไปหรือปล่อยทั้งหมดโดยใช้วิธีการที่เหมาะสม แนวทางนี้เหมาะสำหรับสถานการณ์ที่มีค่าที่ขาดหายไปเล็กน้อย

อย่างไรก็ตาม จะทำอย่างไรเมื่อมีค่าที่หายไปมากเกินไป เช่น เกิน 50%? ในสถานการณ์เช่นนี้ คุณสามารถตั้งค่าขีดจำกัดและใช้วิธีอัตราส่วนค่าที่ขาดหายไปได้ ยิ่งค่าธรณีสัณฐานสูงเท่าไร ขนาดของมิติก็จะยิ่งรุนแรงมากขึ้นเท่านั้น หากเปอร์เซ็นต์ของค่าที่ขาดหายไปในตัวแปรเกินขีดจำกัด คุณสามารถปล่อยตัวแปรนั้นได้

โดยทั่วไป คอลัมน์ข้อมูลที่มีค่าที่หายไปจำนวนมากแทบจะไม่มีข้อมูลที่เป็นประโยชน์ ดังนั้น คุณสามารถลบคอลัมน์ข้อมูลทั้งหมดที่มีค่าที่ขาดหายไปสูงกว่าเกณฑ์ที่ตั้งไว้ได้

6. ตัวกรองความแปรปรวนต่ำ

เช่นเดียวกับที่คุณใช้วิธีการอัตราส่วนค่าที่หายไปสำหรับตัวแปรที่หายไป ดังนั้นสำหรับตัวแปรคงที่ ก็มีเทคนิคตัวกรองความแปรปรวนต่ำ เมื่อชุดข้อมูลมีตัวแปรคงที่ จะไม่สามารถปรับปรุงประสิทธิภาพของโมเดลได้ ทำไม? เพราะมันมีความแปรปรวนเป็นศูนย์

ในวิธีนี้ คุณยังสามารถตั้งค่าขีดจำกัดเพื่อแยกตัวแปรคงที่ทั้งหมดออก ดังนั้น คอลัมน์ข้อมูลทั้งหมดที่มีความแปรปรวนต่ำกว่าค่าเกณฑ์จะถูกตัดออก อย่างไรก็ตาม สิ่งหนึ่งที่คุณต้องจำไว้เกี่ยวกับวิธีการกรองความแปรปรวนต่ำคือความแปรปรวนนั้นขึ้นอยู่กับช่วง ดังนั้น การปรับให้เป็นมาตรฐานจึงเป็นสิ่งจำเป็นก่อนที่จะใช้เทคนิคการลดขนาดมิตินี้

7. ตัวกรองสหสัมพันธ์สูง

หากชุดข้อมูลประกอบด้วยคอลัมน์ข้อมูลที่มีรูปแบบ/แนวโน้มที่คล้ายกันจำนวนมาก คอลัมน์ข้อมูลเหล่านี้มักมีข้อมูลที่เหมือนกัน นอกจากนี้ ขนาดที่แสดงความสัมพันธ์ที่สูงขึ้นอาจส่งผลเสียต่อประสิทธิภาพของโมเดล ในกรณีเช่นนี้ ตัวแปรตัวใดตัวหนึ่งก็เพียงพอที่จะป้อนโมเดล ML

สำหรับสถานการณ์ดังกล่าว ควรใช้เมทริกซ์สหสัมพันธ์แบบเพียร์สันเพื่อระบุตัวแปรที่แสดงความสัมพันธ์สูง เมื่อระบุได้แล้ว คุณสามารถเลือกหนึ่งในนั้นได้โดยใช้ VIF (Variance Inflation Factor) คุณสามารถลบตัวแปรทั้งหมดที่มีค่าสูงกว่า ( VIF > 5 ) ในวิธีนี้ คุณต้องคำนวณสัมประสิทธิ์สหสัมพันธ์ระหว่างคอลัมน์ตัวเลข ( สัมประสิทธิ์โมเมนต์ผลิตภัณฑ์ของเพียร์สัน ) และระหว่างคอลัมน์ที่ระบุ ( ค่า ไคสแควร์ของเพียร์สัน ) ที่นี่ ทุกคู่ของคอลัมน์ที่มีค่าสัมประสิทธิ์สหสัมพันธ์สูงกว่าเกณฑ์ที่ตั้งไว้จะลดลงเป็น 1

เนื่องจากสหสัมพันธ์มีความไวต่อมาตราส่วน คุณต้องทำการนอร์มัลไลซ์คอลัมน์

8. การกำจัดคุณสมบัติย้อนหลัง

ในเทคนิคการขจัดคุณสมบัติย้อนกลับ คุณต้องเริ่มต้นด้วยมิติ 'n' ทั้งหมด ดังนั้น ในการทำซ้ำที่กำหนด คุณสามารถฝึกอัลกอริธึมการจำแนกประเภทเฉพาะซึ่งได้รับการฝึกอบรมเกี่ยวกับ คุณลักษณะอินพุต n รายการ ตอนนี้ คุณต้องลบหนึ่งคุณสมบัติอินพุตในแต่ละครั้ง และฝึกโมเดลเดียวกันบน ตัวแปรอินพุต n-1 n ครั้ง จากนั้น คุณจะลบตัวแปรอินพุตซึ่งการขจัดออกซึ่งสร้างอัตราการผิดพลาดที่เพิ่มขึ้นน้อยที่สุด ซึ่งทิ้ง คุณลักษณะอินพุต n-1 ไว้ นอกจากนี้ คุณทำการจำแนกประเภทซ้ำโดยใช้ คุณลักษณะ n-2 และการดำเนินการนี้จะดำเนินต่อไปจนกว่าจะไม่สามารถลบตัวแปรอื่นได้

การวนซ้ำแต่ละครั้ง ( k) จะสร้างแบบจำลองที่ได้รับการฝึกอบรมเกี่ยวกับคุณลักษณะ nk ที่มีอัตราข้อผิดพลาด e(k ) ต่อจากนี้ คุณต้องเลือกอัตราข้อผิดพลาดสูงสุดที่รับได้เพื่อกำหนดคุณลักษณะจำนวนน้อยที่สุดที่จำเป็นในการเข้าถึงประสิทธิภาพการจัดหมวดหมู่นั้นด้วยอัลกอริธึม ML ที่กำหนด

อ่านเพิ่มเติม: ทำไมการวิเคราะห์ข้อมูลจึงมีความสำคัญในธุรกิจ

9. ไปข้างหน้าคุณสมบัติการก่อสร้าง

การสร้างคุณลักษณะไปข้างหน้าเป็นสิ่งที่ตรงกันข้ามกับวิธีการกำจัดคุณลักษณะย้อนหลัง ในวิธีสร้างคุณลักษณะแบบไปข้างหน้า คุณจะเริ่มด้วยคุณลักษณะหนึ่งคุณลักษณะและดำเนินการต่อไปโดยเพิ่มคุณลักษณะทีละรายการ (ซึ่งเป็นตัวแปรที่ส่งผลให้มีการเพิ่มประสิทธิภาพสูงสุด)

ทั้งการสร้างคุณสมบัติไปข้างหน้าและการกำจัดคุณสมบัติย้อนกลับนั้นใช้เวลาและการคำนวณมาก วิธีการเหล่านี้เหมาะที่สุดสำหรับชุดข้อมูลที่มีคอลัมน์อินพุตจำนวนน้อยอยู่แล้ว

10. ป่าสุ่ม

ฟอเรสต์สุ่มไม่ได้เป็นเพียงตัวแยกประเภทที่ยอดเยี่ยมเท่านั้น แต่ยังมีประโยชน์อย่างมากสำหรับการเลือกคุณสมบัติด้วย ในแนวทางการลดขนาดลงนี้ คุณต้องสร้างเครือข่ายต้นไม้ที่กว้างขวางโดยเทียบกับแอตทริบิวต์เป้าหมายอย่างระมัดระวัง ตัวอย่างเช่น คุณสามารถสร้างชุดต้นไม้ตื้นขนาดใหญ่ (เช่น 2000) (เช่น มี 2 ระดับ) โดยที่ต้นไม้แต่ละต้นจะได้รับการฝึกเป็นเศษส่วนเล็กน้อย (3) ของจำนวนแอตทริบิวต์ทั้งหมด

จุดมุ่งหมายคือการใช้สถิติการใช้งานของแต่ละแอตทริบิวต์เพื่อระบุชุดย่อยของคุณลักษณะที่มีข้อมูลมากที่สุด หากพบว่าแอตทริบิวต์เป็นการแยกที่ดีที่สุด มักจะมีคุณลักษณะข้อมูลที่ควรค่าแก่การพิจารณา เมื่อคุณคำนวณคะแนนของสถิติการใช้งานของแอตทริบิวต์ในฟอเรสต์สุ่มที่สัมพันธ์กับแอตทริบิวต์อื่นๆ แอตทริบิวต์นี้จะให้แอตทริบิวต์ที่คาดการณ์ได้มากที่สุด

บทสรุป

สรุปได้ว่า เมื่อพูดถึงการลดขนาด ไม่มีเทคนิคใดดีที่สุด แต่ละคนมีนิสัยใจคอและข้อดีของมัน ดังนั้น วิธีที่ดีที่สุดในการใช้เทคนิคการลดขนาดคือการใช้การทดลองที่เป็นระบบและควบคุม เพื่อหาว่าเทคนิคใดที่ใช้ได้กับแบบจำลองของคุณและวิธีใดให้ประสิทธิภาพดีที่สุดในชุดข้อมูลที่กำหนด

หากคุณสนใจที่จะเรียนรู้เพิ่มเติมเกี่ยวกับแมชชีนเลิร์นนิง โปรดดูที่ IIIT-B & upGrad's PG Diploma in Machine Learning & AI ซึ่งออกแบบมาสำหรับมืออาชีพที่ทำงานและมีการฝึกอบรมที่เข้มงวดมากกว่า 450 ชั่วโมง กรณีศึกษาและการมอบหมายมากกว่า 30 รายการ IIIT- สถานะศิษย์เก่า B, 5+ โครงการหลักที่ใช้งานได้จริง & ความช่วยเหลือด้านงานกับบริษัทชั้นนำ