Le 10 migliori tecniche di riduzione della dimensionalità per l'apprendimento automatico

Ogni secondo, il mondo genera un volume di dati senza precedenti. Poiché i dati sono diventati una componente cruciale delle aziende e delle organizzazioni in tutti i settori, è essenziale elaborarli, analizzarli e visualizzarli in modo appropriato per estrarre informazioni significative da grandi set di dati. Tuttavia, c'è un problema: più non significa sempre produttivo e accurato. Più dati produciamo ogni secondo, più difficile è analizzarli e visualizzarli per trarre inferenze valide.

È qui che entra in gioco la riduzione della dimensionalità .

Che cos'è la riduzione della dimensionalità?

In parole semplici, la riduzione della dimensionalità si riferisce alla tecnica di riduzione della dimensione di un insieme di caratteristiche di dati. Di solito, i set di dati di apprendimento automatico (set di funzionalità) contengono centinaia di colonne (ad esempio, funzionalità) o una matrice di punti, creando una sfera enorme in uno spazio tridimensionale. Applicando la riduzione della dimensionalità è possibile diminuire o ridurre il numero di colonne a conteggi quantificabili, trasformando così la sfera tridimensionale in un oggetto bidimensionale (cerchio).

Ora viene la domanda, perché devi ridurre le colonne in un set di dati quando puoi inserirlo direttamente in un algoritmo ML e lasciare che risolva tutto da solo?

La maledizione della dimensionalità impone l'applicazione della riduzione della dimensionalità .

La maledizione della dimensionalità

La maledizione della dimensionalità è un fenomeno che si verifica quando si lavora (analizza e visualizza) con dati in spazi ad alta dimensione che non esistono in spazi a bassa dimensione.

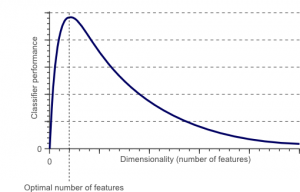
Fonte

Maggiore è il numero di caratteristiche o fattori (ovvero variabili) in un set di funzionalità, più difficile diventa visualizzare il set di allenamento e lavorarci sopra. Un altro punto fondamentale da considerare è che la maggior parte delle variabili sono spesso correlate. Quindi, se consideri ogni variabile all'interno del set di funzionalità, includerai molti fattori ridondanti nel set di allenamento.

Inoltre, più variabili hai a portata di mano, maggiore sarà il numero di campioni per rappresentare tutte le possibili combinazioni di valori delle caratteristiche nell'esempio. Quando il numero di variabili aumenta, il modello diventa più complesso, aumentando così la probabilità di overfitting. Quando si addestra un modello ML su un set di dati di grandi dimensioni contenente molte funzionalità, è destinato a dipendere dai dati di addestramento. Ciò si tradurrà in un modello sovradimensionato che non riesce a funzionare bene sui dati reali.

L'obiettivo principale della riduzione della dimensionalità è evitare l'overfitting. Un dato di addestramento con caratteristiche considerevolmente minori assicurerà che il tuo modello rimanga semplice: farà ipotesi più piccole.

Oltre a questo, la riduzione della dimensionalità ha molti altri vantaggi, come ad esempio:

• Elimina il rumore e le funzioni ridondanti.
• Aiuta a migliorare la precisione e le prestazioni del modello.
• Facilita l'uso di algoritmi che non sono adatti a dimensioni più sostanziali.
• Riduce la quantità di spazio di archiviazione richiesta (meno dati richiedono meno spazio di archiviazione).
• Comprime i dati, riducendo i tempi di calcolo e facilitando un training più rapido dei dati.

Leggi: Cos'è l'analisi discriminante lineare

Tecniche di riduzione della dimensionalità

Le tecniche di riduzione della dimensionalità possono essere classificate in due grandi categorie:

1. Selezione delle funzioni

Il metodo di selezione delle caratteristiche mira a trovare un sottoinsieme delle variabili di input (che sono più rilevanti) dal dataset originale. La selezione delle funzionalità include tre strategie, vale a dire:

• Strategia di filtro
• Strategia del wrapper
• Strategia incorporata

2. Estrazione delle caratteristiche

L'estrazione delle caratteristiche, nota anche come proiezione delle caratteristiche, converte i dati dallo spazio ad alta dimensione in uno con dimensioni minori. Questa trasformazione dei dati può essere lineare o anche non lineare. Questa tecnica trova un insieme più piccolo di nuove variabili, ognuna delle quali è una combinazione di variabili di input (contenenti le stesse informazioni delle variabili di input).

Senza ulteriori indugi, tuffiamoci in una discussione dettagliata di alcune tecniche di riduzione della dimensionalità comunemente usate!

1. Analisi dei componenti principali (PCA)

L'analisi delle componenti principali è una delle principali tecniche lineari di riduzione della dimensionalità. Questo metodo esegue una mappatura diretta dei dati in uno spazio dimensionale minore in modo da massimizzare la varianza dei dati nella rappresentazione a bassa dimensione.

In sostanza, è una procedura statistica che converte ortogonalmente le ' n' coordinate di un insieme di dati in un nuovo insieme di n coordinate, noto come i componenti principali. Questa conversione comporta la creazione della prima componente principale avente la massima varianza. Ogni componente principale successiva sopporta la massima varianza possibile, a condizione che sia ortogonale (non correlata) alle componenti precedenti.

La conversione PCA è sensibile al ridimensionamento relativo delle variabili originali. Pertanto, gli intervalli di colonne di dati devono essere prima normalizzati prima di implementare il metodo PCA. Un'altra cosa da ricordare è che l'utilizzo dell'approccio PCA farà perdere al tuo set di dati la sua interpretabilità. Quindi, se l'interpretabilità è fondamentale per la tua analisi, PCA non è il metodo di riduzione della dimensionalità giusto per il tuo progetto.

2. Fattorizzazione a matrice non negativa (NMF)

NMF scompone una matrice non negativa nel prodotto di due non negative. Questo è ciò che rende il metodo NMF uno strumento prezioso in aree che riguardano principalmente i segnali non negativi (ad esempio, l'astronomia). La regola di aggiornamento moltiplicativo di Lee & Seung ha migliorato la tecnica NMF includendo le incertezze, considerando i dati mancanti e il calcolo parallelo e la costruzione sequenziale.

Queste inclusioni hanno contribuito a rendere stabile e lineare l'approccio NMF. A differenza di PCA, NMF non elimina la media delle matrici, creando così flussi non fisici non negativi. Pertanto, NMF può conservare più informazioni rispetto al metodo PCA.

L'NMF sequenziale è caratterizzato da una base di componenti stabile durante la costruzione e da un processo di modellazione lineare. Questo lo rende lo strumento perfetto in astronomia. L'NMF sequenziale può preservare il flusso nell'imaging diretto delle strutture circumstellari in astronomia, come il rilevamento di esopianeti e l'imaging diretto dei dischi circumstellari.

3. Analisi discriminante lineare (LDA)

L'analisi discriminante lineare è una generalizzazione del metodo discriminante lineare di Fisher ampiamente applicato in statistica, riconoscimento di modelli e apprendimento automatico. La tecnica LDA mira a trovare una combinazione lineare di caratteristiche in grado di caratterizzare o differenziare tra due o più classi di oggetti. LDA rappresenta i dati in un modo che massimizza la separabilità delle classi. Mentre gli oggetti appartenenti alla stessa classe sono giustapposti tramite proiezione, gli oggetti di classi diverse sono disposti molto distanti.

4. Analisi discriminante generalizzata (GDA)

L'analisi discriminante generalizzata è un'analisi discriminante non lineare che sfrutta l'operatore della funzione kernel. La sua teoria alla base corrisponde molto strettamente a quella delle macchine vettoriali di supporto (SVM), in modo tale che la tecnica GDA aiuta a mappare i vettori di input in uno spazio delle caratteristiche ad alta dimensione. Proprio come l'approccio LDA, GDA cerca anche di trovare una proiezione per le variabili in uno spazio di dimensioni inferiori massimizzando il rapporto tra la dispersione tra classi e la dispersione all'interno della classe.

5. Rapporto valori mancanti

Quando esplori un determinato set di dati, potresti scoprire che mancano alcuni valori nel set di dati. Il primo passo nell'affrontare i valori mancanti è identificare il motivo dietro di essi. Di conseguenza, è quindi possibile imputare i valori mancanti o eliminarli del tutto utilizzando i metodi appropriati. Questo approccio è perfetto per le situazioni in cui mancano alcuni valori.

Tuttavia, cosa fare quando ci sono troppi valori mancanti, diciamo, oltre il 50%? In tali situazioni, è possibile impostare un valore di soglia e utilizzare il metodo del rapporto dei valori mancanti. Maggiore è il valore di soglia, più aggressiva sarà la riduzione della dimensionalità. Se la percentuale di valori mancanti in una variabile supera la soglia, è possibile eliminare la variabile.

In genere, le colonne di dati con numerosi valori mancanti difficilmente contengono informazioni utili. Quindi, puoi rimuovere tutte le colonne di dati con valori mancanti superiori alla soglia impostata.

6. Filtro a bassa varianza

Proprio come si utilizza il metodo del rapporto dei valori mancanti per le variabili mancanti, così per le variabili costanti esiste la tecnica del filtro a bassa varianza. Quando un set di dati ha variabili costanti, non è possibile migliorare le prestazioni del modello. Come mai? Perché ha varianza zero.

Anche in questo metodo è possibile impostare un valore di soglia per eliminare tutte le variabili costanti. Verranno quindi eliminate tutte le colonne di dati con varianza inferiore al valore di soglia. Tuttavia, una cosa che devi ricordare sul metodo del filtro a bassa varianza è che la varianza dipende dall'intervallo. Pertanto, la normalizzazione è un must prima di implementare questa tecnica di riduzione della dimensionalità.

7. Filtro ad alta correlazione

Se un set di dati è costituito da colonne di dati con molti modelli/tendenze simili, è molto probabile che queste colonne di dati contengano informazioni identiche. Inoltre, le dimensioni che descrivono una correlazione più elevata possono influire negativamente sulle prestazioni del modello. In tal caso, una di queste variabili è sufficiente per alimentare il modello ML.

Per tali situazioni, è meglio utilizzare la matrice di correlazione di Pearson per identificare le variabili che mostrano un'elevata correlazione. Una volta identificati, è possibile selezionarne uno utilizzando il VIF (Variance Inflation Factor). È possibile rimuovere tutte le variabili di valore superiore ( VIF > 5 ). In questo approccio, devi calcolare il coefficiente di correlazione tra colonne numeriche ( Pearson's Product Moment Coefficient ) e tra colonne nominali ( Pearson's chi-square value ). Qui tutte le coppie di colonne aventi un coefficiente di correlazione superiore alla soglia impostata verranno ridotte a 1.

Poiché la correlazione è sensibile alla scala, è necessario eseguire la normalizzazione delle colonne.

8. Eliminazione delle funzionalità all'indietro

Nella tecnica di eliminazione delle caratteristiche all'indietro, devi iniziare con tutte le 'n' dimensioni. Pertanto, a una data iterazione, è possibile addestrare uno specifico algoritmo di classificazione su n funzioni di input. Ora, devi rimuovere una funzione di input alla volta e addestrare lo stesso modello su n-1 variabili di input n volte. Quindi rimuovi la variabile di input la cui eliminazione genera il più piccolo aumento del tasso di errore, lasciando dietro di sé n-1 funzioni di input. Inoltre, ripeti la classificazione utilizzando n-2 funzioni e ciò continua fino a quando non è possibile rimuovere nessun'altra variabile.

Ogni iterazione ( k) crea un modello addestrato su nk feature con un tasso di errore di e(k) . Successivamente, è necessario selezionare il tasso di errore massimo sopportabile per definire il numero minimo di caratteristiche necessarie per raggiungere quella prestazione di classificazione con l'algoritmo ML specificato.

Leggi anche: Perché l'analisi dei dati è importante negli affari

9. Costruzione delle funzioni avanzate

La costruzione delle feature in avanti è l'opposto del metodo di eliminazione delle feature all'indietro. Nel metodo di costruzione delle feature in avanti, inizi con una feature e continui a progredire aggiungendo una feature alla volta (questa è la variabile che si traduce nel maggiore incremento delle prestazioni).

Sia la costruzione di funzionalità avanzate che l'eliminazione delle funzionalità all'indietro richiedono molto tempo e calcolo. Questi metodi sono più adatti per set di dati che hanno già un numero ridotto di colonne di input.

10. Foreste casuali

Le foreste casuali non sono solo eccellenti classificatori, ma sono anche estremamente utili per la selezione delle caratteristiche. In questo approccio di riduzione della dimensionalità, devi costruire con cura una vasta rete di alberi rispetto a un attributo target. Ad esempio, puoi creare un grande insieme (diciamo, 2000) di alberi poco profondi (diciamo, con due livelli), in cui ogni albero è addestrato su una frazione minore (3) del numero totale di attributi.

L'obiettivo è utilizzare le statistiche di utilizzo di ciascun attributo per identificare il sottoinsieme di funzionalità più informativo. Se un attributo risulta essere la suddivisione migliore, di solito contiene una caratteristica informativa degna di considerazione. Quando si calcola il punteggio delle statistiche di utilizzo di un attributo nella foresta casuale in relazione ad altri attributi, vengono forniti gli attributi più predittivi.

Conclusione

Per concludere, quando si tratta di riduzione della dimensionalità, nessuna tecnica è la migliore in assoluto. Ognuno ha le sue peculiarità e vantaggi. Pertanto, il modo migliore per implementare le tecniche di riduzione della dimensionalità è utilizzare esperimenti sistematici e controllati per capire quale tecnica o quali tecniche funzionano con il modello e quale offre le migliori prestazioni su un determinato set di dati.

Se sei interessato a saperne di più sull'apprendimento automatico, dai un'occhiata al Diploma PG di IIIT-B e upGrad in Machine Learning e AI, progettato per i professionisti che lavorano e offre oltre 450 ore di formazione rigorosa, oltre 30 casi di studio e incarichi, IIIT- B Status di Alumni, oltre 5 progetti pratici pratici e assistenza sul lavoro con le migliori aziende.