10 najlepszych technik redukcji wymiarów dla uczenia maszynowego

W każdej sekundzie świat generuje bezprecedensową ilość danych. Ponieważ dane stały się kluczowym elementem firm i organizacji we wszystkich branżach, niezbędne jest ich odpowiednie przetwarzanie, analizowanie i wizualizowanie, aby wydobyć znaczące wnioski z dużych zbiorów danych. Jest jednak pewien haczyk – więcej nie zawsze oznacza produktywność i dokładność. Im więcej danych produkujemy w każdej sekundzie, tym trudniej jest je analizować i wizualizować w celu wyciągnięcia prawidłowych wniosków.

W tym miejscu w grę wchodzi Redukcja Wymiarowości .

Co to jest redukcja wymiarowości?

W prostych słowach redukcja wymiarowości odnosi się do techniki zmniejszania wymiaru zestawu cech danych. Zazwyczaj zestawy danych uczenia maszynowego (zestaw funkcji) zawierają setki kolumn (tj. funkcji) lub tablicę punktów, tworząc ogromną sferę w trójwymiarowej przestrzeni. Stosując redukcję wymiarów , możesz zmniejszyć lub zmniejszyć liczbę kolumn do policzalnych wartości, przekształcając w ten sposób trójwymiarową sferę w dwuwymiarowy obiekt (koło).

Teraz pojawia się pytanie, dlaczego musisz redukować kolumny w zestawie danych, skoro możesz bezpośrednio wprowadzić je do algorytmu ML i pozwolić mu działać samodzielnie?

Klątwa wymiarowości nakazuje stosowanie redukcji wymiarowości .

Klątwa Wymiarowości

Klątwa wymiarowości to zjawisko, które pojawia się, gdy pracujesz (analizujesz i wizualizujesz) z danymi w przestrzeniach wysokowymiarowych, które nie istnieją w przestrzeniach niskowymiarowych.

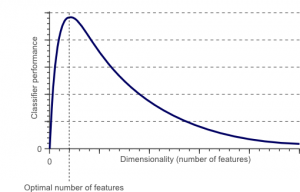
Źródło

Im wyższa jest liczba cech lub czynników (czyli zmiennych) w zestawie cech, tym trudniej jest zwizualizować zestaw uczący i pracować nad nim. Inną ważną kwestią do rozważenia jest to, że większość zmiennych jest często skorelowana. Tak więc, jeśli myślisz, że każda zmienna w zestawie funkcji, w zestawie uczącym będzie zawierać wiele nadmiarowych czynników.

Co więcej, im więcej zmiennych masz pod ręką, tym większa będzie liczba próbek reprezentujących wszystkie możliwe kombinacje wartości cech w przykładzie. Wraz ze wzrostem liczby zmiennych model stanie się bardziej złożony, zwiększając w ten sposób prawdopodobieństwo nadmiernego dopasowania. Gdy trenujesz model ML na dużym zestawie danych zawierającym wiele funkcji, musi on być zależny od danych szkoleniowych. Skutkiem tego będzie przesadnie dopasowany model, który nie będzie dobrze działał na rzeczywistych danych.

Podstawowym celem redukcji wymiarowości jest uniknięcie nadmiernego dopasowania. Dane treningowe o znacznie mniejszych funkcjach sprawią, że Twój model pozostanie prosty – będzie zawierał mniejsze założenia.

Poza tym redukcja wymiarowości ma wiele innych korzyści, takich jak:

• Eliminuje hałas i zbędne funkcje.
• Pomaga poprawić dokładność i wydajność modelu.
• Ułatwia korzystanie z algorytmów, które nie nadają się do większych wymiarów.
• Zmniejsza ilość wymaganej przestrzeni dyskowej (mniej danych wymaga mniejszej przestrzeni dyskowej).
• Kompresuje dane, co skraca czas obliczeń i ułatwia szybsze trenowanie danych.

Przeczytaj: Czym jest liniowa analiza dyskryminacyjna ?

Techniki redukcji wymiarowości

Techniki redukcji wymiarowości można podzielić na dwie szerokie kategorie:

1. Wybór funkcji

Metoda wyboru cech ma na celu znalezienie podzbioru zmiennych wejściowych (które są najbardziej odpowiednie) z oryginalnego zbioru danych. Wybór funkcji obejmuje trzy strategie, a mianowicie:

• Strategia filtrowania
• Strategia opakowania
• Wbudowana strategia

2. Ekstrakcja funkcji

Ekstrakcja cech, czyli rzutowanie cech, konwertuje dane z przestrzeni wielowymiarowej do przestrzeni o mniejszych wymiarach. Ta transformacja danych może być liniowa lub nieliniowa. Technika ta znajduje mniejszy zestaw nowych zmiennych, z których każda jest kombinacją zmiennych wejściowych (zawierających te same informacje co zmienne wejściowe).

Bez dalszych ceregieli przejdźmy do szczegółowego omówienia kilku powszechnie stosowanych technik redukcji wymiarów!

1. Analiza głównych składowych (PCA)

Analiza głównych składowych jest jedną z wiodących liniowych technik redukcji wymiarowości. Ta metoda wykonuje bezpośrednie mapowanie danych do mniejszej przestrzeni wymiarowej w sposób, który maksymalizuje wariancję danych w reprezentacji niskowymiarowej.

Zasadniczo jest to procedura statystyczna, która ortogonalnie przekształca współrzędne „ n” zbioru danych na nowy zestaw współrzędnych n , znanych jako składowe główne. Ta konwersja powoduje utworzenie pierwszego głównego składnika o maksymalnej wariancji. Każdy kolejny składnik główny ma najwyższą możliwą wariancję, pod warunkiem, że jest ortogonalny (nie skorelowany) z poprzednimi składnikami.

Konwersja PCA jest wrażliwa na względne skalowanie oryginalnych zmiennych. W związku z tym zakresy kolumn danych muszą najpierw zostać znormalizowane przed wdrożeniem metody PCA. Inną rzeczą, o której należy pamiętać, jest to, że korzystanie z podejścia PCA spowoduje, że zestaw danych straci swoją interpretację. Tak więc, jeśli interpretacja jest kluczowa dla twojej analizy, PCA nie jest właściwą metodą redukcji wymiarowości dla twojego projektu.

2. Nieujemna faktoryzacja macierzy (NMF)

NMF rozkłada nieujemną macierz na iloczyn dwóch nieujemnych. To sprawia, że ​​metoda NMF jest cennym narzędziem w dziedzinach, które dotyczą przede wszystkim sygnałów nieujemnych (np. astronomii). Zasada aktualizacji multiplikatywnej autorstwa Lee & Seung ulepszyła technikę NMF poprzez – uwzględnienie niepewności, uwzględnienie brakujących danych i obliczeń równoległych oraz konstrukcję sekwencyjną.

Wtrącenia te przyczyniły się do ustabilizowania i liniowego podejścia NMF. W przeciwieństwie do PCA, NMF nie eliminuje średniej macierzy, tworząc w ten sposób niefizyczne nieujemne strumienie. W ten sposób NMF może zachować więcej informacji niż metoda PCA.

Sekwencyjny NMF charakteryzuje się stabilną bazą komponentów podczas budowy oraz liniowym procesem modelowania. To czyni go idealnym narzędziem w astronomii. Sekwencyjne NMF może zachować płynność w bezpośrednim obrazowaniu struktur okołogwiazdowych w astronomii, na przykład w wykrywaniu egzoplanet i bezpośrednim obrazowaniu dysków okołogwiazdowych.

3. Liniowa analiza dyskryminacyjna (LDA)

Liniowa analiza dyskryminacyjna jest uogólnieniem liniowej metody dyskryminacyjnej Fishera, która jest szeroko stosowana w statystyce, rozpoznawaniu wzorców i uczeniu maszynowym. Technika LDA ma na celu znalezienie liniowej kombinacji cech, które mogą charakteryzować lub rozróżniać dwie lub więcej klas obiektów. LDA reprezentuje dane w sposób, który maksymalizuje rozdzielność klas. Podczas gdy obiekty należące do tej samej klasy są zestawiane za pomocą projekcji, obiekty z różnych klas są rozmieszczone daleko od siebie.

4. Uogólniona analiza dyskryminacyjna (GDA)

Uogólniona analiza dyskryminacyjna jest nieliniową analizą dyskryminacyjną, która wykorzystuje operator funkcji jądra. Jego podstawowa teoria jest bardzo zbliżona do teorii maszyn wektorów nośnych (SVM), tak że technika GDA pomaga mapować wektory wejściowe w wielowymiarowej przestrzeni cech. Podobnie jak podejście LDA, GDA również stara się znaleźć projekcję dla zmiennych w przestrzeni o niższych wymiarach, maksymalizując stosunek rozpraszania między klasami do rozpraszania wewnątrz klasy.

5. Stosunek brakujących wartości

Podczas eksploracji danego zestawu danych może się okazać, że w zestawie danych brakuje niektórych wartości. Pierwszym krokiem w radzeniu sobie z brakującymi wartościami jest zidentyfikowanie ich przyczyny. W związku z tym możesz następnie przypisać brakujące wartości lub całkowicie je usunąć, korzystając z odpowiednich metod. To podejście jest idealne w sytuacjach, gdy brakuje kilku wartości.

Co jednak zrobić, gdy brakuje wartości, powiedzmy, ponad 50%? W takich sytuacjach można ustawić wartość progową i zastosować metodę współczynnika braków danych. Im wyższa wartość progowa, tym bardziej agresywna będzie redukcja wymiarowości. Jeśli procent braków danych w zmiennej przekracza próg, możesz usunąć zmienną.

Ogólnie rzecz biorąc, kolumny danych z licznymi brakami danych prawie nie zawierają przydatnych informacji. Możesz więc usunąć wszystkie kolumny danych, w których brakujące wartości są wyższe niż ustawiony próg.

6. Filtr niskiej wariancji

Tak jak używasz metody współczynnika braków danych dla brakujących zmiennych, tak dla zmiennych stałych istnieje technika filtrowania niskiej wariancji. Gdy zestaw danych zawiera zmienne stałe, nie można poprawić wydajności modelu. Czemu? Ponieważ ma zerową wariancję.

W tej metodzie również można ustawić wartość progową, aby odłączyć wszystkie zmienne stałe. Tak więc wszystkie kolumny danych z wariancją mniejszą niż wartość progowa zostaną wyeliminowane. Jednak jedną rzeczą, o której musisz pamiętać w metodzie filtra o niskiej wariancji, jest to, że wariancja jest zależna od zakresu. Dlatego normalizacja jest koniecznością przed wdrożeniem tej techniki redukcji wymiarowości.

7. Filtr wysokiej korelacji

Jeśli zestaw danych składa się z kolumn danych o wielu podobnych wzorcach/trendach, istnieje duże prawdopodobieństwo, że te kolumny danych będą zawierać identyczne informacje. Ponadto wymiary, które przedstawiają wyższą korelację, mogą niekorzystnie wpłynąć na wydajność modelu. W takim przypadku jedna z tych zmiennych wystarczy do zasilania modelu ML.

W takich sytuacjach najlepiej jest użyć macierzy korelacji Pearsona do zidentyfikowania zmiennych wykazujących wysoką korelację. Po ich zidentyfikowaniu możesz wybrać jeden z nich za pomocą VIF (Wariancji współczynnika inflacji). Możesz usunąć wszystkie zmienne o wyższej wartości ( VIF > 5 ). W tym podejściu należy obliczyć współczynnik korelacji między kolumnami liczbowymi ( Iloczyn Pearsona ) i między kolumnami nominalnymi ( wartość chi-kwadrat Pearsona ). Tutaj wszystkie pary kolumn o współczynniku korelacji wyższym niż ustawiony próg zostaną zredukowane do 1.

Ponieważ korelacja jest zależna od skali, należy przeprowadzić normalizację kolumn.

8. Eliminacja funkcji wstecznych

W technice wstecznej eliminacji cech musisz zacząć od wszystkich wymiarów 'n'. W ten sposób w danej iteracji można wytrenować określony algorytm klasyfikacji na n cechach wejściowych. Teraz musisz usuwać jedną cechę wejściową na raz i trenować ten sam model na n-1 zmiennych wejściowych n razy. Następnie usuwamy zmienną wejściową, której eliminacja generuje najmniejszy wzrost stopy błędów, co pozostawia n-1 cech wejściowych. Co więcej, powtarzasz klasyfikację przy użyciu n-2 cech i to trwa do momentu, gdy żadna inna zmienna nie może zostać usunięta.

Każda iteracja ( k) tworzy model wyszkolony na nk cechach o współczynniku błędu e(k) . Następnie należy wybrać maksymalną dopuszczalną stopę błędów, aby zdefiniować najmniejszą liczbę cech potrzebnych do osiągnięcia tej wydajności klasyfikacji przy danym algorytmie ML.

Przeczytaj także: Dlaczego analiza danych jest ważna w biznesie

9. Budowa funkcji do przodu

Konstrukcja przedniej cechy jest przeciwieństwem metody eliminacji cech wstecz. W metodzie konstruowania elementów do przodu, zaczynasz od jednej funkcji i kontynuujesz postęp, dodając jedną funkcję na raz (jest to zmienna, która daje największy wzrost wydajności).

Zarówno konstrukcja elementów do przodu, jak i eliminacja elementów wstecznych są czasochłonne i czasochłonne. Te metody najlepiej nadają się do zestawów danych, które mają już małą liczbę kolumn wejściowych.

10. Losowe lasy

Losowe lasy są nie tylko doskonałymi klasyfikatorami, ale są również niezwykle przydatne do wyboru cech. W tym podejściu redukcji wymiarowości musisz ostrożnie zbudować rozległą sieć drzew w odniesieniu do atrybutu docelowego. Na przykład, możesz stworzyć duży zestaw (powiedzmy 2000) płytkich drzew (powiedzmy, mających dwa poziomy), gdzie każde drzewo jest wytrenowane na mniejszym ułamku (3) całkowitej liczby atrybutów.

Celem jest wykorzystanie statystyk użytkowania każdego atrybutu w celu zidentyfikowania najbardziej pouczającego podzbioru cech. Jeśli okaże się, że atrybut jest najlepszym podziałem, zazwyczaj zawiera on informację, którą warto rozważyć. Obliczenie wyniku statystyk użycia atrybutu w losowym lesie w stosunku do innych atrybutów daje najbardziej przewidywalne atrybuty.

Wniosek

Podsumowując, jeśli chodzi o redukcję wymiarowości, żadna technika nie jest absolutnie najlepsza. Każdy ma swoje dziwactwa i zalety. Dlatego najlepszym sposobem na wdrożenie technik redukcji wymiarów jest użycie systematycznych i kontrolowanych eksperymentów w celu ustalenia, która technika (techniki) działa z Twoim modelem i która zapewnia najlepszą wydajność na danym zbiorze danych.

Jeśli chcesz dowiedzieć się więcej o uczeniu maszynowym, sprawdź dyplom PG IIIT-B i upGrad w uczeniu maszynowym i sztucznej inteligencji, który jest przeznaczony dla pracujących profesjonalistów i oferuje ponad 450 godzin rygorystycznego szkolenia, ponad 30 studiów przypadków i zadań, IIIT- Status absolwenta B, ponad 5 praktycznych, praktycznych projektów zwieńczenia i pomoc w pracy z najlepszymi firmami.