Top 10 tehnici de reducere a dimensionalității pentru învățarea automată

În fiecare secundă, lumea generează un volum de date fără precedent. Deoarece datele au devenit o componentă crucială a afacerilor și organizațiilor din toate industriile, este esențial să le procesăm, să le analizați și să le vizualizați în mod corespunzător pentru a extrage informații semnificative din seturi mari de date. Cu toate acestea, există o captură – mai mult nu înseamnă întotdeauna productiv și precis. Cu cât producem mai multe date în fiecare secundă, cu atât este mai dificil să le analizăm și să le vizualizam pentru a trage concluzii valide.

Aici intervine Reducerea Dimensionalității .

Ce este reducerea dimensionalității?

Cu cuvinte simple, reducerea dimensionalității se referă la tehnica de reducere a dimensiunii unui set de caracteristici de date. De obicei, seturile de date de învățare automată (setul de caracteristici) conțin sute de coloane (adică, caracteristici) sau o serie de puncte, creând o sferă masivă într-un spațiu tridimensional. Prin aplicarea reducerii dimensionalității , puteți reduce sau reduce numărul de coloane la numărări cuantificabile, transformând astfel sfera tridimensională într-un obiect bidimensional (cerc).

Acum vine întrebarea, de ce trebuie să reduceți coloanele dintr-un set de date când îl puteți introduce direct într-un algoritm ML și îl lăsați să rezolve totul de la sine?

Blestemul dimensionalității impune aplicarea reducerii dimensionalității .

Blestemul dimensionalității

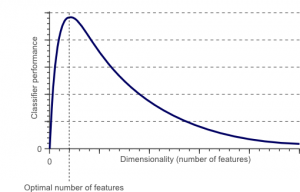
Blestemul dimensionalității este un fenomen care apare atunci când lucrați (analizați și vizualizați) cu date în spații de dimensiuni mari care nu există în spații de dimensiuni joase.

Sursă

Cu cât este mai mare numărul de caracteristici sau factori (aka variabile) dintr-un set de caracteristici, cu atât devine mai dificil să vizualizați setul de antrenament și să lucrați la el. Un alt punct vital de luat în considerare este faptul că majoritatea variabilelor sunt adesea corelate. Deci, dacă credeți că fiecare variabilă din setul de caracteristici, veți include mulți factori redundanți în setul de antrenament.

În plus, cu cât aveți mai multe variabile la îndemână, cu atât va fi mai mare numărul de eșantioane pentru a reprezenta toate combinațiile posibile de valori ale caracteristicilor din exemplu. Când numărul de variabile crește, modelul va deveni mai complex, crescând astfel probabilitatea de supraadaptare. Atunci când antrenați un model ML pe un set de date mare care conține multe caracteristici, este neapărat să depindă de datele de antrenament. Acest lucru va avea ca rezultat un model supraadaptat care nu reușește să funcționeze bine pe datele reale.

Scopul principal al reducerii dimensionalității este evitarea supraajustării. Datele de antrenament cu caracteristici considerabil mai mici se vor asigura că modelul dumneavoastră rămâne simplu – va face presupuneri mai mici.

În afară de aceasta, reducerea dimensionalității are multe alte beneficii, cum ar fi:

• Elimină zgomotul și funcțiile redundante.
• Ajută la îmbunătățirea preciziei și a performanței modelului.
• Facilitează utilizarea algoritmilor care nu sunt potriviți pentru dimensiuni mai substanțiale.
• Reduce cantitatea de spațiu de stocare necesară (mai puține date necesită mai puțin spațiu de stocare).
• Comprimă datele, ceea ce reduce timpul de calcul și facilitează antrenamentul mai rapid al datelor.

Citiți: Ce este analiza discriminantă ineară

Tehnici de reducere a dimensionalității

Tehnicile de reducere a dimensionalității pot fi clasificate în două mari categorii:

1. Selectarea caracteristicilor

Metoda de selecție a caracteristicilor își propune să găsească un subset al variabilelor de intrare (care sunt cele mai relevante) din setul de date original. Selectarea caracteristicilor include trei strategii, și anume:

• Strategia de filtrare
• Strategia Wrapper
• Strategie încorporată

2. Extragerea caracteristicilor

Extragerea caracteristicilor, aka, proiecția caracteristicilor, convertește datele din spațiul de dimensiuni mari într-unul cu dimensiuni mai mici. Această transformare a datelor poate fi fie liniară, fie poate fi și neliniară. Această tehnică găsește un set mai mic de variabile noi, fiecare dintre acestea fiind o combinație de variabile de intrare (conținând aceleași informații ca și variabilele de intrare).

Fără alte prelungiri, să ne aruncăm într-o discuție detaliată a câtorva tehnici de reducere a dimensionalității utilizate în mod obișnuit!

1. Analiza componentelor principale (PCA)

Analiza componentelor principale este una dintre principalele tehnici liniare de reducere a dimensionalității. Această metodă realizează o mapare directă a datelor într-un spațiu dimensional mai mic într-un mod care maximizează varianța datelor în reprezentarea cu dimensiuni reduse.

În esență, este o procedură statistică care convertește ortogonal coordonatele „ n” ale unui set de date într-un nou set de n coordonate, cunoscut sub numele de componente principale. Această conversie are ca rezultat crearea primei componente principale care are variația maximă. Fiecare componentă principală care urmează are cea mai mare variație posibilă, cu condiția ca aceasta să fie ortogonală (nu corelată) cu componentele precedente.

Conversia PCA este sensibilă la scalarea relativă a variabilelor originale. Astfel, intervalele coloanelor de date trebuie mai întâi normalizate înainte de implementarea metodei PCA. Un alt lucru de reținut este că utilizarea abordării PCA va face ca setul de date să-și piardă interpretabilitatea. Deci, dacă interpretabilitatea este crucială pentru analiza dvs., PCA nu este metoda potrivită de reducere a dimensionalității pentru proiectul dvs.

2. Factorizarea matricei nenegative (NMF)

NMF descompune o matrice nenegativă în produsul a două matrice nenegative. Acesta este ceea ce face ca metoda NMF să fie un instrument valoros în domeniile care se preocupă în primul rând de semnale nenegative (de exemplu, astronomie). Regula de actualizare multiplicativă a lui Lee & Seung a îmbunătățit tehnica NMF prin – inclusiv incertitudinile, luând în considerare datele lipsă și calculul paralel și construcția secvențială.

Aceste incluziuni au contribuit la a face abordarea NMF stabilă și liniară. Spre deosebire de PCA, NMF nu elimină media matricelor, creând astfel fluxuri nefizice nenegative. Astfel, NMF poate păstra mai multe informații decât metoda PCA.

NMF secvenţial se caracterizează printr-o bază stabilă a componentelor în timpul construcţiei şi un proces de modelare liniară. Acest lucru îl face instrumentul perfect în astronomie. NMF secvențial poate păstra fluxul în imagistica directă a structurilor circumstelare în astronomie, cum ar fi detectarea exoplanetelor și imagistica directă a discurilor circumstelare.

3. Analiza discriminantă liniară (LDA)

Analiza discriminantă liniară este o generalizare a metodei discriminante liniară a lui Fisher, care este aplicată pe scară largă în statistică, recunoaștere a modelelor și învățarea automată. Tehnica LDA își propune să găsească o combinație liniară de caracteristici care pot caracteriza sau diferenția între două sau mai multe clase de obiecte. LDA reprezintă datele într-un mod care maximizează separabilitatea claselor. În timp ce obiectele aparținând aceleiași clase sunt juxtapuse prin proiecție, obiectele din clase diferite sunt aranjate la distanță.

4. Analiza discriminantă generalizată (GDA)

Analiza discriminantă generalizată este o analiză discriminantă neliniară care folosește operatorul funcției nucleu. Teoria sa de bază se potrivește foarte strâns cu cea a mașinilor vectoriale de suport (SVM), astfel încât tehnica GDA ajută la maparea vectorilor de intrare în spațiul caracteristic de înaltă dimensiune. La fel ca abordarea LDA, GDA caută, de asemenea, să găsească o proiecție pentru variabile într-un spațiu de dimensiuni inferioare prin maximizarea raportului dintre împrăștierea dintre clase și împrăștierea în interiorul clasei.

5. Raportul valorilor lipsă

Când explorați un anumit set de date, este posibil să descoperiți că lipsesc anumite valori în setul de date. Primul pas în tratarea valorilor lipsă este identificarea motivului din spatele acestora. În consecință, puteți apoi să atribuiți valorile lipsă sau să le renunțați cu totul utilizând metodele potrivite. Această abordare este perfectă pentru situațiile în care lipsesc câteva valori.

Totuși, ce să faci când lipsesc prea multe valori, să zicem, peste 50%? În astfel de situații, puteți seta o valoare de prag și puteți utiliza metoda raportului valorilor lipsă. Cu cât valoarea pragului este mai mare, cu atât mai agresivă va fi reducerea dimensionalității. Dacă procentul de valori lipsă dintr-o variabilă depășește pragul, puteți renunța la variabila.

În general, coloanele de date care au numeroase valori lipsă conțin cu greu informații utile. Deci, puteți elimina toate coloanele de date care au valori lipsă mai mari decât pragul setat.

6. Filtru de variație scăzută

Așa cum utilizați metoda raportului de valori lipsă pentru variabilele lipsă, la fel pentru variabilele constante, există tehnica de filtrare a varianței scăzute. Când un set de date are variabile constante, nu este posibilă îmbunătățirea performanței modelului. De ce? Pentru că are varianță zero.

De asemenea, în această metodă, puteți seta o valoare de prag pentru a elimina toate variabilele constante. Deci, toate coloanele de date cu varianță mai mică decât valoarea de prag vor fi eliminate. Cu toate acestea, un lucru pe care trebuie să-l rețineți despre metoda filtrului cu variație scăzută este că varianța depinde de interval. Astfel, normalizarea este o necesitate înainte de implementarea acestei tehnici de reducere a dimensionalității.

7. Filtru de corelație ridicată

Dacă un set de date constă din coloane de date care au multe modele/tendințe similare, este foarte probabil ca aceste coloane de date să conțină informații identice. De asemenea, dimensiunile care descriu o corelație mai mare pot avea un impact negativ asupra performanței modelului. Într-un astfel de caz, una dintre aceste variabile este suficientă pentru a alimenta modelul ML.

Pentru astfel de situații, cel mai bine este să utilizați matricea de corelație Pearson pentru a identifica variabilele care prezintă o corelație ridicată. Odată identificate, puteți selecta una dintre ele folosind VIF (Variance Inflation Factor). Puteți elimina toate variabilele care au o valoare mai mare ( VIF > 5 ). În această abordare, trebuie să calculați coeficientul de corelație dintre coloanele numerice ( Coeficientul de moment al produsului Pearson ) și între coloanele nominale ( valoarea chi-pătratului lui Pearson ). Aici, toate perechile de coloane care au un coeficient de corelație mai mare decât pragul setat vor fi reduse la 1.

Deoarece corelația este sensibilă la scară, trebuie să efectuați normalizarea coloanei.

8. Eliminare caracteristică înapoi

În tehnica de eliminare a caracteristicilor înapoi, trebuie să începeți cu toate dimensiunile „n”. Astfel, la o anumită iterație, puteți antrena un anumit algoritm de clasificare care este antrenat pe n caracteristici de intrare. Acum, trebuie să eliminați câte o caracteristică de intrare și să antrenați același model pe n-1 variabile de intrare de n ori. Apoi eliminați variabila de intrare a cărei eliminare generează cea mai mică creștere a ratei de eroare, care lasă în urmă n-1 caracteristici de intrare. În plus, repetați clasificarea folosind n-2 caracteristici și aceasta continuă până când nicio altă variabilă nu poate fi eliminată.

Fiecare iterație ( k) creează un model antrenat pe nk caracteristici având o rată de eroare de e(k) . După aceasta, trebuie să selectați rata maximă de eroare suportabilă pentru a defini cel mai mic număr de caracteristici necesare pentru a atinge acea performanță de clasificare cu algoritmul ML dat.

Citește și: De ce este importantă analiza datelor în afaceri

9. Construcție caracteristică înainte

Construcția caracteristicilor înainte este opusă metodei de eliminare a caracteristicilor înapoi. În metoda de construire a caracteristicilor înainte, începeți cu o caracteristică și continuați să progresați adăugând câte o caracteristică la un moment dat (aceasta este variabila care are ca rezultat cea mai mare creștere a performanței).

Atât construcția înainte de caracteristici, cât și eliminarea caracteristicilor înapoi necesită timp și calcul intensiv. Aceste metode sunt cele mai potrivite pentru seturile de date care au deja un număr redus de coloane de intrare.

10. Păduri aleatorii

Pădurile aleatorii nu sunt doar clasificatoare excelente, ci sunt și extrem de utile pentru selectarea caracteristicilor. În această abordare de reducere a dimensionalității, trebuie să construiți cu atenție o rețea extinsă de arbori împotriva unui atribut țintă. De exemplu, puteți crea un set mare (să zicem, 2000) de copaci de mică adâncime (să zicem, având două niveluri), în care fiecare copac este antrenat pe o fracțiune minoră (3) din numărul total de atribute.

Scopul este de a utiliza statisticile de utilizare ale fiecărui atribut pentru a identifica cel mai informativ subset de caracteristici. Dacă se consideră că un atribut este cea mai bună împărțire, de obicei conține o caracteristică informativă care merită luată în considerare. Când calculați scorul statisticilor de utilizare a unui atribut în pădurea aleatoare în raport cu alte atribute, vă oferă cele mai predictive atribute.

Concluzie

În concluzie, când vine vorba de reducerea dimensionalității, nicio tehnică nu este absolut cea mai bună. Fiecare are ciudateniile și avantajele sale. Astfel, cea mai bună modalitate de a implementa tehnici de reducere a dimensionalității este să utilizați experimente sistematice și controlate pentru a afla care tehnică(e) funcționează(e) cu modelul dvs. și care oferă cea mai bună performanță pe un anumit set de date.

Dacă sunteți interesat să aflați mai multe despre învățarea automată, consultați Diploma PG de la IIIT-B și upGrad în Învățare automată și AI, care este concepută pentru profesioniști care lucrează și oferă peste 450 de ore de pregătire riguroasă, peste 30 de studii de caz și sarcini, IIIT- B Statut de absolvenți, peste 5 proiecte practice practice și asistență pentru locuri de muncă cu firme de top.