機械学習の次元削減手法トップ10

毎秒、世界は前例のない量のデータを生成します。 データはすべての業界のビジネスや組織の重要なコンポーネントになっているため、大規模なデータセットから意味のある洞察を抽出するには、データを適切に処理、分析、視覚化することが不可欠です。 ただし、落とし穴があります。それ以上のことは、必ずしも生産的で正確であることを意味するわけではありません。 毎秒生成するデータが多いほど、有効な推論を引き出すためにデータを分析および視覚化することが難しくなります。

ここで次元削減が効果を発揮します。

次元削減とは何ですか？

簡単に言うと、次元削減とは、データ機能セットの次元を削減する手法を指します。 通常、機械学習データセット（機能セット）には、数百の列（つまり、機能）またはポイントの配列が含まれ、3次元空間に巨大な球体を作成します。 次元削減を適用することにより、列の数を定量化可能なカウントに減らすか減らすことができ、それによって3次元の球を2次元のオブジェクト（円）に変換できます。

ここで問題が発生します。データセットをMLアルゴリズムに直接フィードして、それ自体ですべてを処理できるのに、なぜデータセットの列を減らす必要があるのでしょうか。

次元の呪いは、次元削減の適用を義務付けています。

次元の呪い

次元の呪いは、低次元空間には存在しない高次元空間のデータを操作（分析、視覚化）するときに発生する現象です。

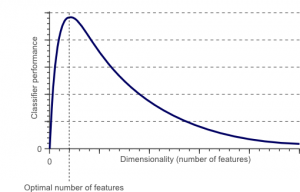
ソース

機能セット内の機能または要素（別名変数）の数が多いほど、トレーニングセットを視覚化して作業することが難しくなります。 考慮すべきもう1つの重要なポイントは、ほとんどの変数が相関していることが多いということです。 したがって、機能セット内のすべての変数を考える場合、トレーニングセットに多くの冗長な要素を含めることになります。

さらに、手元にある変数が多いほど、例の特徴値のすべての可能な組み合わせを表すサンプルの数が多くなります。 変数の数が増えると、モデルはより複雑になり、過剰適合の可能性が高くなります。 多くの機能を含む大規模なデータセットでMLモデルをトレーニングする場合、トレーニングデータに依存することになります。 これにより、実際のデータではうまく機能しない過剰適合モデルが発生します。

次元削減の主な目的は、過剰適合を回避することです。 機能が大幅に少ないトレーニングデータを使用すると、モデルが単純なままであることが保証されます。つまり、仮定が小さくなります。

これとは別に、次元削減には次のような他の多くの利点があります。

• ノイズと冗長機能を排除します。
• モデルの精度とパフォーマンスを向上させるのに役立ちます。
• これにより、より実質的な次元に適さないアルゴリズムの使用が容易になります。
• 必要なストレージスペースの量が減ります（必要なデータが少ないほど、必要なストレージスペースも少なくなります）。
• データを圧縮するため、計算時間が短縮され、データのトレーニングが高速化されます。

読む：L線形判別分析とは

次元削減手法

次元削減手法は、大きく2つのカテゴリに分類できます。

1.特徴選択

特徴選択方法は、元のデータセットから（最も関連性の高い）入力変数のサブセットを見つけることを目的としています。 特徴選択には、次の3つの戦略が含まれます。

• フィルター戦略
• ラッパー戦略
• 組み込み戦略

2.特徴抽出

特徴抽出、別名、特徴投影は、データを高次元の空間からより小さな次元の空間に変換します。 このデータ変換は、線形または非線形のいずれかです。 この手法では、新しい変数のより小さなセットが検出されます。各変数は、入力変数（入力変数と同じ情報を含む）の組み合わせです。

さらに面倒なことはせずに、一般的に使用されるいくつかの次元削減手法の詳細な説明に飛び込みましょう！

1.主成分分析（PCA）

主成分分析は、次元削減の主要な線形手法の1つです。 このメソッドは、低次元表現でのデータの分散を最大化する方法で、データを低次元空間に直接マッピングします。

基本的に、これは、データセットの「 n」座標を主成分と呼ばれる新しいn座標のセットに直交変換する統計手順です。 この変換により、最大の分散を持つ最初の主成分が作成されます。 後続の各主成分は、先行する成分と直交している（相関していない）という条件の下で、可能な限り高い分散を持ちます。

PCA変換は、元の変数の相対的なスケーリングに敏感です。 したがって、PCAメソッドを実装する前に、データ列の範囲を最初に正規化する必要があります。 もう1つ覚えておくべきことは、PCAアプローチを使用すると、データセットの解釈可能性が失われることです。 したがって、解釈可能性が分析にとって重要である場合、PCAはプロジェクトに適した次元削減方法ではありません。

2.非負行列因子分解（NMF）

NMFは、非負行列を2つの非負行列の積に分解します。 これが、NMF法を、主に非負の信号（天文学など）に関係する分野で価値のあるツールにしている理由です。 Lee＆Seungによる乗法更新ルールは、不確実性を含め、欠測データと並列計算を考慮し、順次構築することにより、NMF手法を改善しました。

これらの包含は、NMFアプローチを安定して線形にすることに貢献しました。 PCAとは異なり、NMFは行列の平均を除去しないため、非物理的な非負のフラックスが生成されます。 したがって、NMFはPCA法よりも多くの情報を保持できます。

シーケンシャルNMFは、構築中の安定したコンポーネントベースと線形モデリングプロセスによって特徴付けられます。 これは、天文学の完璧なツールになります。 シーケンシャルNMFは、太陽系外惑星の検出や星周円盤の直接イメージングなど、天文学における星周構造の直接イメージングのフラックスを維持できます。

3.線形判別分析（LDA）

線形判別分析は、統計、パターン認識、機械学習に広く適用されているフィッシャーの線形判別法を一般化したものです。 LDA手法は、2つ以上のクラスのオブジェクトを特徴付けたり区別したりできる機能の線形結合を見つけることを目的としています。 LDAは、クラスの分離可能性を最大化する方法でデータを表します。 同じクラスに属するオブジェクトは投影によって並置されますが、異なるクラスのオブジェクトは遠く離れて配置されます。

4.一般化判別分析（GDA）

一般化判別分析は、カーネル関数演算子を利用する非線形判別分析です。 その基礎となる理論は、サポートベクターマシン（SVM）の理論と非常によく一致しているため、GDA手法は、入力ベクトルを高次元の特徴空間にマッピングするのに役立ちます。 LDAアプローチと同様に、GDAも、クラス間散乱とクラス内散乱の比率を最大化することにより、低次元空間内の変数の射影を見つけようとします。

5.欠測値の比率

特定のデータセットを探索すると、データセットにいくつかの欠落値があることに気付く場合があります。 欠落している値に対処するための最初のステップは、それらの背後にある理由を特定することです。 したがって、適切な方法を使用して、欠落している値を代入したり、それらを完全に削除したりできます。 このアプローチは、いくつかの欠落値がある状況に最適です。

ただし、欠落している値が多すぎる場合、たとえば50％を超える場合は、どうすればよいでしょうか。 このような状況では、しきい値を設定し、欠測値比率法を使用できます。 しきい値が高いほど、次元削減はより積極的になります。 変数の欠落値のパーセンテージがしきい値を超える場合は、変数を削除できます。

一般に、欠落値が多数あるデータ列には、有用な情報がほとんど含まれていません。 したがって、設定されたしきい値よりも高い値が欠落しているすべてのデータ列を削除できます。

6.低分散フィルター

欠測変数に欠測値比率法を使用するのと同じように、定数変数には、低分散フィルター手法があります。 データセットに定数変数がある場合、モデルのパフォーマンスを向上させることはできません。 なんで？ 分散がゼロだからです。

この方法でも、すべての定数変数を切り離すためのしきい値を設定できます。 したがって、分散がしきい値よりも低いすべてのデータ列が削除されます。 ただし、低分散フィルター法について覚えておく必要があることの1つは、分散が範囲に依存することです。 したがって、正規化は、この次元削減手法を実装する前に必須です。

7.高相関フィルター

データセットが多くの類似したパターン/傾向を持つデータ列で構成されている場合、これらのデータ列には同一の情報が含まれている可能性が高くなります。 また、より高い相関関係を表すディメンションは、モデルのパフォーマンスに悪影響を与える可能性があります。 このような場合、これらの変数の1つでMLモデルをフィードできます。

このような状況では、ピアソン相関行列を使用して、高い相関を示す変数を特定するのが最適です。 それらが識別されると、VIF（分散拡大係数）を使用してそれらの1つを選択できます。 より高い値（VIF> 5）を持つすべての変数を削除できます。 このアプローチでは、数値列（ピアソンのカイ二乗係数）と名目列（ピアソンのカイ二乗値）の間の相関係数を計算する必要があります。 ここでは、設定されたしきい値よりも高い相関係数を持つ列のすべてのペアが1に削減されます。

相関はスケールに依存するため、列の正規化を実行する必要があります。

8.後方機能の削除

後方特徴除去手法では、すべての「n」次元から開始する必要があります。 したがって、特定の反復で、特定の分類アルゴリズムをn個の入力特徴でトレーニングすることができます。 ここで、一度に1つの入力特徴を削除し、 n-1個の入力変数で同じモデルをn回トレーニングする必要があります。 次に、エラー率の増加が最小になる入力変数を削除します。これにより、 n-1個の入力機能が残ります。 さらに、 n-2個の機能を使用して分類を繰り返します。これは、他の変数を削除できなくなるまで続きます。

各反復（ k）は、エラー率e（k）を持つnk個の特徴でトレーニングされたモデルを作成します。 これに続いて、最大許容エラー率を選択して、特定のMLアルゴリズムでその分類パフォーマンスに到達するために必要な機能の最小数を定義する必要があります。

また読む：データ分析がビジネスで重要である理由

9.フォワードフィーチャーの構築

前方の特徴の構築は、後方の特徴の除去方法の反対です。 フォワードフィーチャーの構築方法では、1つのフィーチャーから始めて、一度に1つのフィーチャーを追加することで進行を続けます（これは、パフォーマンスの最大の向上をもたらす変数です）。

前方機能の構築と後方機能の除去はどちらも、時間と計算量が多くなります。 これらの方法は、入力列の数がすでに少ないデータセットに最適です。

10.ランダムフォレスト

ランダムフォレストは、優れた分類子であるだけでなく、特徴選択にも非常に役立ちます。 この次元削減アプローチでは、ターゲット属性に対してツリーの広範なネットワークを慎重に構築する必要があります。 たとえば、浅いツリー（たとえば、2つのレベルを持つ）の大規模なセット（たとえば、2000）を作成できます。ここで、各ツリーは、属性の総数のごく一部（3）でトレーニングされます。

目的は、各属性の使用統計を使用して、機能の最も有益なサブセットを識別することです。 属性が最適な分割であることがわかった場合、通常、検討に値する有益な機能が含まれています。 他の属性との関係でランダムフォレスト内の属性の使用統計のスコアを計算すると、最も予測的な属性が得られます。

結論

結論として、次元削減に関しては、絶対に最適な手法はありません。 それぞれに癖と利点があります。 したがって、次元削減手法を実装する最良の方法は、体系的で制御された実験を使用して、どの手法がモデルで機能し、どの手法が特定のデータセットで最高のパフォーマンスを提供するかを把握することです。

機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのPGディプロマをご覧ください。これは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディと課題、IIIT-を提供します。 B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との仕事の支援。