As 10 principais técnicas de redução de dimensionalidade para aprendizado de máquina

A cada segundo, o mundo gera um volume de dados sem precedentes. Como os dados se tornaram um componente crucial de negócios e organizações em todos os setores, é essencial processá-los, analisá-los e visualizá-los adequadamente para extrair insights significativos de grandes conjuntos de dados. No entanto, há um problema – mais nem sempre significa produtivo e preciso. Quanto mais dados produzimos a cada segundo, mais desafiador é analisá-los e visualizá-los para fazer inferências válidas.

É aqui que a Redução de Dimensionalidade entra em ação.

O que é Redução de Dimensionalidade?

Em palavras simples, a redução de dimensionalidade refere-se à técnica de reduzir a dimensão de um conjunto de recursos de dados. Normalmente, conjuntos de dados de aprendizado de máquina (conjunto de recursos) contêm centenas de colunas (ou seja, recursos) ou uma matriz de pontos, criando uma esfera massiva em um espaço tridimensional. Ao aplicar a redução de dimensionalidade , você pode diminuir ou diminuir o número de colunas para contagens quantificáveis, transformando assim a esfera tridimensional em um objeto bidimensional (círculo).

Agora vem a pergunta: por que você deve reduzir as colunas em um conjunto de dados quando pode alimentá-lo diretamente em um algoritmo de ML e deixá-lo resolver tudo sozinho?

A maldição da dimensionalidade exige a aplicação da redução da dimensionalidade .

A Maldição da Dimensionalidade

A maldição da dimensionalidade é um fenômeno que surge quando você trabalha (analisa e visualiza) com dados em espaços de alta dimensão que não existem em espaços de baixa dimensão.

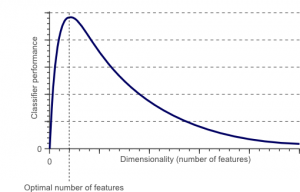
Fonte

Quanto maior o número de recursos ou fatores (também conhecidos como variáveis) em um conjunto de recursos, mais difícil se torna visualizar o conjunto de treinamento e trabalhar nele. Outro ponto vital a considerar é que a maioria das variáveis ​​são frequentemente correlacionadas. Portanto, se você pensar em todas as variáveis ​​do conjunto de recursos, incluirá muitos fatores redundantes no conjunto de treinamento.

Além disso, quanto mais variáveis ​​você tiver em mãos, maior será o número de amostras para representar todas as combinações possíveis de valores de recursos no exemplo. Quando o número de variáveis ​​aumenta, o modelo se torna mais complexo, aumentando assim a probabilidade de overfitting. Quando você treina um modelo de ML em um grande conjunto de dados contendo muitos recursos, ele depende dos dados de treinamento. Isso resultará em um modelo superajustado que não funciona bem em dados reais.

O objetivo principal da redução de dimensionalidade é evitar o overfitting. Dados de treinamento com recursos consideravelmente menores garantirão que seu modelo permaneça simples – ele fará suposições menores.

Além disso, a redução de dimensionalidade tem muitos outros benefícios, como:

• Elimina ruídos e recursos redundantes.
• Ajuda a melhorar a precisão e o desempenho do modelo.
• Facilita o uso de algoritmos inadequados para dimensões mais substanciais.
• Reduz a quantidade de espaço de armazenamento necessária (menos dados precisam de menos espaço de armazenamento).
• Ele compacta os dados, o que reduz o tempo de computação e facilita o treinamento mais rápido dos dados.

Leia: O que é análise discriminante linear

Técnicas de Redução de Dimensionalidade

As técnicas de redução de dimensionalidade podem ser categorizadas em duas grandes categorias:

1. Seleção de recursos

O método de seleção de características visa encontrar um subconjunto das variáveis ​​de entrada (que são mais relevantes) do conjunto de dados original. A seleção de recursos inclui três estratégias, a saber:

• Estratégia de filtro
• Estratégia de wrapper
• Estratégia incorporada

2. Extração de recursos

A extração de recursos, também conhecida como projeção de recursos, converte os dados do espaço de alta dimensão para um com dimensões menores. Essa transformação de dados pode ser linear ou não linear também. Essa técnica encontra um conjunto menor de novas variáveis, cada uma das quais é uma combinação de variáveis ​​de entrada (contendo as mesmas informações que as variáveis ​​de entrada).

Sem mais delongas, vamos mergulhar em uma discussão detalhada de algumas técnicas de redução de dimensionalidade comumente usadas!

1. Análise de Componentes Principais (PCA)

A Análise de Componentes Principais é uma das principais técnicas lineares de redução de dimensionalidade. Este método realiza um mapeamento direto dos dados para um espaço dimensional menor de forma a maximizar a variância dos dados na representação de baixa dimensão.

Essencialmente, é um procedimento estatístico que converte ortogonalmente as ' n' coordenadas de um conjunto de dados em um novo conjunto de n coordenadas, conhecidas como componentes principais. Essa conversão resulta na criação do primeiro componente principal com a variância máxima. Cada componente principal subsequente tem a maior variação possível, sob a condição de que seja ortogonal (não correlacionado) aos componentes anteriores.

A conversão do PCA é sensível ao dimensionamento relativo das variáveis ​​originais. Assim, os intervalos das colunas de dados devem primeiro ser normalizados antes de implementar o método PCA. Outra coisa a lembrar é que usar a abordagem PCA fará com que seu conjunto de dados perca sua interpretabilidade. Portanto, se a interpretabilidade é crucial para sua análise, o PCA não é o método de redução de dimensionalidade correto para o seu projeto.

2. Fatoração matricial não negativa (NMF)

O NMF decompõe uma matriz não negativa no produto de duas não negativas. É isso que torna o método NMF uma ferramenta valiosa em áreas que se preocupam principalmente com sinais não negativos (por exemplo, astronomia). A regra de atualização multiplicativa de Lee & Seung melhorou a técnica de NMF – incluindo incertezas, considerando dados perdidos e computação paralela, e construção sequencial.

Essas inclusões contribuíram para tornar a abordagem NMF estável e linear. Ao contrário do PCA, o NMF não elimina a média das matrizes, criando assim fluxos não-negativos não físicos. Assim, o NMF pode preservar mais informações do que o método PCA.

O NMF sequencial é caracterizado por uma base de componentes estável durante a construção e um processo de modelagem linear. Isso o torna a ferramenta perfeita em astronomia. NMF sequencial pode preservar o fluxo na imagem direta de estruturas circunstelares em astronomia, como a detecção de exoplanetas e imagens diretas de discos circunstelares.

3. Análise discriminante linear (LDA)

A análise discriminante linear é uma generalização do método discriminante linear de Fisher que é amplamente aplicado em estatística, reconhecimento de padrões e aprendizado de máquina. A técnica LDA visa encontrar uma combinação linear de características que possam caracterizar ou diferenciar entre duas ou mais classes de objetos. LDA representa dados de uma forma que maximiza a separabilidade de classes. Enquanto objetos pertencentes à mesma classe são justapostos via projeção, objetos de classes diferentes são dispostos distantes.

4. Análise discriminante generalizada (GDA)

A análise discriminante generalizada é uma análise discriminante não linear que aproveita o operador da função kernel. Sua teoria subjacente se aproxima muito daquela das máquinas de vetores de suporte (SVM), de modo que a técnica GDA ajuda a mapear os vetores de entrada em um espaço de recursos de alta dimensão. Assim como a abordagem LDA, o GDA também procura encontrar uma projeção para variáveis ​​em um espaço de menor dimensão, maximizando a razão de dispersão entre classes para dispersão dentro de classe.

5. Proporção de Valores Omissos

Ao explorar um determinado conjunto de dados, você pode descobrir que há alguns valores ausentes no conjunto de dados. O primeiro passo para lidar com valores ausentes é identificar a razão por trás deles. Assim, você pode imputar os valores ausentes ou eliminá-los completamente usando os métodos adequados. Essa abordagem é perfeita para situações em que há alguns valores ausentes.

No entanto, o que fazer quando há muitos valores ausentes, digamos, acima de 50%? Em tais situações, você pode definir um valor limite e usar o método de razão de valores ausentes. Quanto maior o valor do limiar, mais agressiva será a redução da dimensionalidade. Se a porcentagem de valores ausentes em uma variável exceder o limite, você poderá descartar a variável.

Geralmente, as colunas de dados com vários valores ausentes dificilmente contêm informações úteis. Assim, você pode remover todas as colunas de dados com valores ausentes superiores ao limite definido.

6. Filtro de Baixa Variação

Assim como você usa o método de razão de valores ausentes para variáveis ​​ausentes, para variáveis ​​constantes, existe a técnica de filtro de baixa variância. Quando um conjunto de dados possui variáveis ​​constantes, não é possível melhorar o desempenho do modelo. Por quê? Porque tem variância zero.

Nesse método também, você pode definir um valor limite para eliminar todas as variáveis ​​constantes. Assim, todas as colunas de dados com variância inferior ao valor limite serão eliminadas. No entanto, uma coisa que você deve lembrar sobre o método de filtro de baixa variação é que a variação depende do intervalo. Assim, a normalização é uma obrigação antes de implementar esta técnica de redução de dimensionalidade.

7. Filtro de alta correlação

Se um conjunto de dados consiste em colunas de dados com muitos padrões/tendências semelhantes, é muito provável que essas colunas de dados contenham informações idênticas. Além disso, as dimensões que retratam uma correlação mais alta podem afetar negativamente o desempenho do modelo. Nesse caso, uma dessas variáveis ​​é suficiente para alimentar o modelo de ML.

Para tais situações, é melhor usar a matriz de correlação de Pearson para identificar as variáveis ​​que apresentam uma alta correlação. Uma vez identificados, você pode selecionar um deles usando o VIF (Variance Inflation Factor). Você pode remover todas as variáveis ​​com um valor mais alto ( VIF > 5 ). Nesta abordagem, você deve calcular o coeficiente de correlação entre colunas numéricas ( Coeficiente de Momento do Produto de Pearson ) e entre colunas nominais ( valor qui-quadrado de Pearson ). Aqui, todos os pares de colunas com um coeficiente de correlação superior ao limite definido serão reduzidos para 1.

Como a correlação é sensível à escala, você deve executar a normalização da coluna.

8. Eliminação de recursos para trás

Na técnica de eliminação de recursos para trás, você deve começar com todas as 'n' dimensões. Assim, em uma determinada iteração, você pode treinar um algoritmo de classificação específico que é treinado em n recursos de entrada. Agora, você precisa remover um recurso de entrada por vez e treinar o mesmo modelo em n-1 variáveis ​​de entrada n vezes. Em seguida, você remove a variável de entrada cuja eliminação gera o menor aumento na taxa de erro, o que deixa para trás n-1 recursos de entrada. Além disso, você repete a classificação usando n-2 recursos, e isso continua até que nenhuma outra variável possa ser removida.

Cada iteração ( k) cria um modelo treinado em nk recursos com uma taxa de erro de e(k) . Depois disso, você deve selecionar a taxa de erro máxima suportável para definir o menor número de recursos necessários para alcançar esse desempenho de classificação com o algoritmo de ML fornecido.

Leia também: Por que a análise de dados é importante nos negócios

9. Construção de Recurso Avançado

A construção de recursos para frente é o oposto do método de eliminação de recursos para trás. No método de construção de recursos avançados, você começa com um recurso e continua a progredir adicionando um recurso por vez (essa é a variável que resulta no maior aumento no desempenho).

Tanto a construção de recursos para frente quanto a eliminação de recursos para trás consomem muito tempo e computação. Esses métodos são mais adequados para conjuntos de dados que já possuem um número baixo de colunas de entrada.

10. Florestas Aleatórias

Florestas aleatórias não são apenas excelentes classificadores, mas também são extremamente úteis para a seleção de recursos. Nesta abordagem de redução de dimensionalidade, você deve construir cuidadosamente uma extensa rede de árvores em relação a um atributo de destino. Por exemplo, você pode criar um grande conjunto (digamos, 2000) de árvores rasas (digamos, com dois níveis), onde cada árvore é treinada em uma fração menor (3) do número total de atributos.

O objetivo é usar as estatísticas de uso de cada atributo para identificar o subconjunto de recursos mais informativo. Se um atributo for considerado a melhor divisão, ele geralmente contém um recurso informativo que merece consideração. Quando você calcula a pontuação das estatísticas de uso de um atributo na floresta aleatória em relação a outros atributos, ela fornece os atributos mais preditivos.

Conclusão

Para concluir, quando se trata de redução de dimensionalidade, nenhuma técnica é a melhor absoluta. Cada um tem suas peculiaridades e vantagens. Assim, a melhor maneira de implementar técnicas de redução de dimensionalidade é usar experimentos sistemáticos e controlados para descobrir qual(is) técnica(s) funciona(m) com seu modelo e qual oferece o melhor desempenho em um determinado conjunto de dados.

Se você estiver interessado em aprender mais sobre aprendizado de máquina, confira o PG Diploma in Machine Learning & AI do IIIT-B e upGrad, projetado para profissionais que trabalham e oferece mais de 450 horas de treinamento rigoroso, mais de 30 estudos de caso e atribuições, IIIT- B Status de ex-aluno, mais de 5 projetos práticos práticos e assistência de trabalho com as principais empresas.