أهم 10 تقنيات لتقليل الأبعاد لتعلم الآلة

في كل ثانية ، يولد العالم حجمًا غير مسبوق من البيانات. نظرًا لأن البيانات أصبحت مكونًا مهمًا للشركات والمؤسسات في جميع الصناعات ، فمن الضروري معالجتها وتحليلها وتصورها بشكل مناسب لاستخراج رؤى ذات مغزى من مجموعات البيانات الكبيرة. ومع ذلك ، هناك مشكلة - فالمزيد لا يعني دائمًا الإنتاجية والدقة. كلما زاد عدد البيانات التي ننتجها في كل ثانية ، زاد صعوبة تحليلها وتصورها لاستخلاص استنتاجات صحيحة.

هذا هو المكان الذي يلعب فيه تقليل الأبعاد .

ما هو تقليل الأبعاد؟

بكلمات بسيطة ، يشير تقليل الأبعاد إلى تقنية تقليل أبعاد مجموعة ميزات البيانات. عادةً ما تحتوي مجموعات بيانات التعلم الآلي (مجموعة الميزات) على مئات الأعمدة (أي الميزات) أو مجموعة من النقاط ، مما يؤدي إلى إنشاء كرة ضخمة في مساحة ثلاثية الأبعاد. من خلال تطبيق تقليل الأبعاد ، يمكنك تقليل أو تقليل عدد الأعمدة إلى أعداد قابلة للقياس الكمي ، وبالتالي تحويل الكرة ثلاثية الأبعاد إلى كائن ثنائي الأبعاد (دائرة).

يأتي الآن السؤال ، لماذا يجب عليك تقليل الأعمدة في مجموعة البيانات عندما يمكنك إدخالها مباشرة في خوارزمية ML والسماح لها بالعمل في كل شيء بمفردها؟

تلزم لعنة الأبعاد تطبيق تقليل الأبعاد .

لعنة الأبعاد

لعنة الأبعاد ظاهرة تظهر عندما تعمل (تحلل وتتخيل) مع بيانات في مساحات عالية الأبعاد لا توجد في المساحات منخفضة الأبعاد.

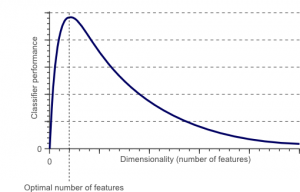
مصدر

كلما زاد عدد الميزات أو العوامل (المعروفة أيضًا باسم المتغيرات) في مجموعة الميزات ، كلما أصبح من الصعب تصور مجموعة التدريب والعمل عليها. هناك نقطة حيوية أخرى يجب مراعاتها وهي أن معظم المتغيرات غالبًا ما تكون مترابطة. لذلك ، إذا كنت تعتقد أن كل متغير ضمن مجموعة الميزات ، فسوف تقوم بتضمين العديد من العوامل الزائدة في مجموعة التدريب.

علاوة على ذلك ، كلما زاد عدد المتغيرات المتوفرة لديك ، زاد عدد العينات لتمثيل جميع المجموعات الممكنة لقيم الميزة في المثال. عندما يزداد عدد المتغيرات ، سيصبح النموذج أكثر تعقيدًا ، مما يزيد من احتمالية التجهيز الزائد. عندما تقوم بتدريب نموذج ML على مجموعة بيانات كبيرة تحتوي على العديد من الميزات ، فمن المحتم أن يعتمد على بيانات التدريب. سينتج عن ذلك نموذج مُجهز بشكل زائد يفشل في الأداء الجيد على البيانات الحقيقية.

الهدف الأساسي لتقليل الأبعاد هو تجنب فرط التجهيز. ستضمن بيانات التدريب ذات الميزات الأقل إلى حد كبير أن يظل نموذجك بسيطًا - ستضع افتراضات أصغر.

بصرف النظر عن هذا ، فإن لتقليل الأبعاد العديد من الفوائد الأخرى ، مثل:

• يزيل الضوضاء والميزات الزائدة عن الحاجة.
• يساعد على تحسين دقة النموذج وأدائه.
• يسهل استخدام الخوارزميات غير الملائمة لأبعاد أكثر جوهرية.
• يقلل من مقدار مساحة التخزين المطلوبة (تحتاج البيانات الأقل إلى مساحة تخزين أقل).
• يقوم بضغط البيانات ، مما يقلل من وقت الحساب ويسهل تدريب البيانات بشكل أسرع.

قراءة: ما هو تحليل تمييزي في L inear

تقنيات تقليل الأبعاد

يمكن تصنيف تقنيات تقليل الأبعاد إلى فئتين رئيسيتين:

1. اختيار الميزة

تهدف طريقة اختيار الميزة إلى العثور على مجموعة فرعية من متغيرات الإدخال (الأكثر صلة) من مجموعة البيانات الأصلية. يتضمن اختيار الميزة ثلاث استراتيجيات ، وهي:

• استراتيجية التصفية
• استراتيجية التغليف
• استراتيجية مضمنة

2. ميزة استخراج

يعمل استخراج الميزة ، المعروف أيضًا باسم إسقاط الميزة ، على تحويل البيانات من الفضاء عالي الأبعاد إلى مساحة ذات أبعاد أقل. قد يكون تحويل البيانات هذا إما خطيًا أو قد يكون غير خطي أيضًا. تجد هذه التقنية مجموعة أصغر من المتغيرات الجديدة ، كل منها عبارة عن مجموعة من متغيرات الإدخال (تحتوي على نفس المعلومات مثل متغيرات الإدخال).

بدون مزيد من اللغط ، دعنا نتعمق في مناقشة تفصيلية لبعض تقنيات تقليل الأبعاد الشائعة الاستخدام!

1. تحليل المكونات الرئيسية (PCA)

يعد تحليل المكون الرئيسي أحد الأساليب الخطية الرائدة لتقليل الأبعاد. تقوم هذه الطريقة بإجراء تعيين مباشر للبيانات إلى مساحة ذات أبعاد أقل بطريقة تزيد من تباين البيانات في التمثيل منخفض الأبعاد.

بشكل أساسي ، هو إجراء إحصائي يحول بشكل متعامد الإحداثيات 'n' لمجموعة البيانات إلى مجموعة جديدة من إحداثيات n ، والمعروفة باسم المكونات الرئيسية. ينتج عن هذا التحويل إنشاء أول مكون رئيسي له أقصى تباين. يحمل كل مكون رئيسي لاحق أعلى تباين ممكن ، بشرط أن يكون متعامدًا (غير مرتبط) بالمكونات السابقة.

يعتبر تحويل PCA حساسًا للقياس النسبي للمتغيرات الأصلية. وبالتالي ، يجب أولاً تسوية نطاقات أعمدة البيانات قبل تنفيذ طريقة PCA. شيء آخر يجب تذكره هو أن استخدام نهج PCA سيجعل مجموعة البيانات الخاصة بك تفقد قابليتها للتفسير. لذلك ، إذا كانت القابلية للتفسير ضرورية لتحليلك ، فإن PCA ليست طريقة تقليل الأبعاد الصحيحة لمشروعك.

2. عامل المصفوفة غير السلبي (NMF)

NMF يقسم المصفوفة غير السالبة إلى حاصل ضرب اثنين غير سالبين. هذا ما يجعل طريقة NMF أداة قيمة في المجالات التي تهتم بشكل أساسي بالإشارات غير السلبية (على سبيل المثال ، علم الفلك). حسنت قاعدة التحديث المضاعف من قبل Lee & Seung تقنية NMF من خلال - بما في ذلك عدم اليقين ، والنظر في البيانات المفقودة والحساب المتوازي ، والبناء المتسلسل.

ساهمت هذه الادراج في جعل نهج NMF مستقرًا وخطيًا. على عكس PCA ، لا يلغي NMF متوسط ​​المصفوفات ، وبالتالي يخلق تدفقات غير مادية غير سلبية. وبالتالي ، يمكن لـ NMF الاحتفاظ بمعلومات أكثر من طريقة PCA.

يتميز NMF المتسلسل بقاعدة مكونات مستقرة أثناء البناء وعملية النمذجة الخطية. هذا يجعلها الأداة المثالية في علم الفلك. يمكن أن يحافظ NMF المتسلسل على التدفق في التصوير المباشر للهياكل الظرفية في علم الفلك ، مثل اكتشاف الكواكب الخارجية والتصوير المباشر للأقراص المحيطة بالنجوم.

3. تحليل التمايز الخطي (LDA)

التحليل التمييزي الخطي هو تعميم لطريقة فيشر التمييزية الخطية التي يتم تطبيقها على نطاق واسع في الإحصاء ، والتعرف على الأنماط ، والتعلم الآلي. تهدف تقنية LDA إلى إيجاد مجموعة خطية من الميزات التي يمكن أن تميز أو تفرق بين فئتين أو أكثر من الكائنات. يمثل LDA البيانات بطريقة تزيد من إمكانية فصل الفئات. بينما يتم وضع الكائنات التي تنتمي إلى نفس الفئة جنبًا إلى جنب عبر الإسقاط ، يتم ترتيب الكائنات من فئات مختلفة بشكل متباعد.

4. التحليل التمييزي المعمم (GDA)

التحليل المميز المعمم هو تحليل تمييزي غير خطي يعزز عامل وظيفة النواة. تتطابق نظريتها الأساسية بشكل وثيق مع نظريتها الخاصة بآلات ناقلات الدعم (SVM) ، بحيث تساعد تقنية GDA في تعيين متجهات الإدخال في مساحة ميزة عالية الأبعاد. تمامًا مثل نهج LDA ، يسعى GDA أيضًا إلى إيجاد إسقاط للمتغيرات في مساحة ذات أبعاد أقل من خلال زيادة نسبة المشتتات بين الفئات إلى التشتت داخل الفصل.

5. نسبة القيم المفقودة

عند استكشاف مجموعة بيانات معينة ، قد تجد أن هناك بعض القيم المفقودة في مجموعة البيانات. الخطوة الأولى في التعامل مع القيم المفقودة هي تحديد السبب وراءها. وفقًا لذلك ، يمكنك عندئذٍ نسب القيم المفقودة أو إسقاطها تمامًا باستخدام الطرق الملائمة. هذا النهج مثالي للمواقف التي يكون فيها بعض القيم المفقودة.

ومع ذلك ، ماذا تفعل عندما يكون هناك عدد كبير جدًا من القيم المفقودة ، على سبيل المثال ، أكثر من 50٪؟ في مثل هذه الحالات ، يمكنك تعيين قيمة عتبة واستخدام طريقة نسبة القيم المفقودة. كلما زادت قيمة العتبة ، زادت حدة تقليل الأبعاد. إذا تجاوزت النسبة المئوية للقيم المفقودة في متغير الحد ، يمكنك إسقاط المتغير.

بشكل عام ، لا تحتوي أعمدة البيانات التي تحتوي على العديد من القيم المفقودة على معلومات مفيدة. لذلك ، يمكنك إزالة جميع أعمدة البيانات التي تحتوي على قيم مفقودة أعلى من الحد المعين.

6. مرشح التباين المنخفض

تمامًا كما تستخدم طريقة نسبة القيم المفقودة للمتغيرات المفقودة ، لذلك بالنسبة للمتغيرات الثابتة ، هناك تقنية مرشح التباين المنخفض. عندما تحتوي مجموعة البيانات على متغيرات ثابتة ، لا يمكن تحسين أداء النموذج. لماذا ا؟ لأنها لا تحتوي على أي تباين.

في هذه الطريقة أيضًا ، يمكنك تعيين قيمة حدية لاستبعاد جميع المتغيرات الثابتة. لذلك ، سيتم حذف جميع أعمدة البيانات ذات التباين الأقل من قيمة العتبة. ومع ذلك ، هناك شيء واحد يجب أن تتذكره حول طريقة مرشح التباين المنخفض وهو أن التباين يعتمد على النطاق. وبالتالي ، فإن التطبيع أمر لا بد منه قبل تنفيذ تقنية تقليل الأبعاد هذه.

7. مرشح الارتباط العالي

إذا كانت مجموعة البيانات تتكون من أعمدة بيانات بها الكثير من الأنماط / الاتجاهات المتشابهة ، فمن المرجح أن تحتوي أعمدة البيانات هذه على معلومات متطابقة. أيضًا ، يمكن أن تؤثر الأبعاد التي تصور ارتباطًا أعلى سلبًا على أداء النموذج. في مثل هذه الحالة ، يكفي أحد هذه المتغيرات لتغذية نموذج ML.

في مثل هذه المواقف ، من الأفضل استخدام مصفوفة ارتباط بيرسون لتحديد المتغيرات التي تظهر ارتباطًا عاليًا. بمجرد تحديدهم ، يمكنك تحديد واحد منهم باستخدام VIF (عامل تضخم التباين). يمكنك إزالة جميع المتغيرات التي لها قيمة أعلى (VIF> 5). في هذا الأسلوب ، عليك حساب معامل الارتباط بين الأعمدة العددية ( معامل لحظة المنتج لبيرسون ) وبين الأعمدة الاسمية ( قيمة مربع كاي لبيرسون ). هنا ، سيتم تقليل جميع أزواج الأعمدة التي لها معامل ارتباط أعلى من العتبة المحددة إلى 1.

نظرًا لأن الارتباط حساس للمقياس ، يجب إجراء تسوية العمود.

8. إزالة الميزة الخلفية

في تقنية حذف الميزة الخلفية ، عليك أن تبدأ بجميع الأبعاد "n". وبالتالي ، في تكرار معين ، يمكنك تدريب خوارزمية تصنيف محددة يتم تدريبها على ميزات الإدخال n . الآن ، يجب عليك إزالة ميزة إدخال واحدة في كل مرة وتدريب نفس النموذج على متغيرات الإدخال n-1 n مرة. ثم تقوم بإزالة متغير الإدخال الذي ينتج عن حذفه أصغر زيادة في معدل الخطأ ، مما يترك وراءه ميزات الإدخال n-1 . علاوة على ذلك ، تكرر التصنيف باستخدام ميزات n-2 ، ويستمر هذا حتى لا يمكن إزالة أي متغير آخر.

ينشئ كل تكرار ( k) نموذجًا مدربًا على ميزات nk ذات معدل خطأ e (k) . بعد ذلك ، يجب عليك تحديد الحد الأقصى لمعدل الخطأ المحتمل لتحديد أصغر عدد من الميزات اللازمة للوصول إلى أداء التصنيف هذا باستخدام خوارزمية ML المحددة.

اقرأ أيضًا: لماذا تحليل البيانات مهم في الأعمال

9. بناء ميزة إلى الأمام

بناء الميزة الأمامية هو عكس طريقة حذف الميزة الخلفية. في طريقة إنشاء الميزة الأمامية ، تبدأ بميزة واحدة وتستمر في التقدم بإضافة ميزة واحدة في كل مرة (هذا هو المتغير الذي ينتج عنه أكبر دفعة في الأداء).

يتطلب كل من إنشاء الميزات الأمامية وإلغاء الميزة الخلفية وقتًا وحسابًا مكثفًا. هذه الطرق هي الأنسب لمجموعات البيانات التي تحتوي بالفعل على عدد قليل من أعمدة الإدخال.

10. غابات عشوائية

الغابات العشوائية ليست فقط مصنفات ممتازة ولكنها أيضًا مفيدة للغاية في اختيار الميزات. في نهج تقليل الأبعاد هذا ، يجب عليك إنشاء شبكة واسعة من الأشجار بعناية مقابل سمة مستهدفة. على سبيل المثال ، يمكنك إنشاء مجموعة كبيرة (على سبيل المثال ، 2000) من الأشجار الضحلة (على سبيل المثال ، تحتوي على مستويين) ، حيث يتم تدريب كل شجرة على جزء صغير (3) من إجمالي عدد السمات.

الهدف هو استخدام إحصائيات استخدام كل سمة لتحديد المجموعة الفرعية الأكثر إفادة من الميزات. إذا تم العثور على إحدى السمات على أنها أفضل تقسيم ، فعادة ما تحتوي على ميزة إعلامية تستحق الدراسة. عندما تحسب درجة إحصائيات استخدام إحدى السمات في الغابة العشوائية فيما يتعلق بالسمات الأخرى ، فإنها تمنحك السمات الأكثر توقعًا.

خاتمة

في الختام ، عندما يتعلق الأمر بتقليل الأبعاد ، لا توجد تقنية هي الأفضل على الإطلاق. لكل منها مزاياها ومزاياها. وبالتالي ، فإن أفضل طريقة لتنفيذ تقنيات تقليل الأبعاد هي استخدام تجارب منهجية وخاضعة للرقابة لمعرفة التقنية (التقنيات) التي تعمل مع نموذجك والتي تقدم أفضل أداء لمجموعة بيانات معينة.

إذا كنت مهتمًا بمعرفة المزيد حول التعلم الآلي ، فراجع دبلوم PG في IIIT-B & upGrad في التعلم الآلي والذكاء الاصطناعي المصمم للمهنيين العاملين ويقدم أكثر من 450 ساعة من التدريب الصارم ، وأكثر من 30 دراسة حالة ومهمة ، IIIT- حالة الخريجين B ، أكثر من 5 مشاريع تتويجا عملية ومساعدة وظيفية مع أفضل الشركات.