Veri Yapısında İfade Ayrıştırma: Notasyon Türleri, İlişkilendirme ve Öncelik

Ayrıştırma , doğal dillerde veya bilgisayar dillerinde ifade edilen ve biçimsel dilbilgisine uygun olarak ifade edilen bir dizi simgeyi analiz etme sürecidir . Veri Yapısında İfade Ayrıştırma , aritmetik ve mantıksal ifadelerin değerlendirilmesi anlamına gelir. İlk önce, bir aritmetik ifadenin nasıl yazıldığını görelim:

• 9+9
• Cb

Bir ifade, operatör veya parantez işlevi görebilecek sabitler, değişkenler ve sembollerle yazılabilir. Tüm bu ifadelerin belirli bir dizi kurala uyması gerekir. Bu kurala göre ifadenin ayrıştırılması dilbilgisine göre yapılır.

Aritmetik bir ifade, Notasyon biçiminde ifade edilir . Aritmetikte bir ifade yazmanın üç yolu vardır:

• Infix Notasyonu
• Önek (Lehçe) Gösterimi
• Postfix (Ters-Lehçe) Notasyonu

Ancak ifade yazıldığında istenilen ifadenin çıktısı aynı kalır. Gösterim türlerine başlamadan önce, Veri Yapısında Ayrıştırma ifadesinde İlişkilendirme ve Öncelik'in ne olduğuna bakalım.

Yeni başlayan biriyseniz ve veri bilimi hakkında daha fazla bilgi edinmek istiyorsanız, en iyi üniversitelerden veri bilimi kurslarımıza göz atın.

Okuyun: Veri Yapısındaki Grafikler

çağrışım

Başlamadan önce, Associativity özelliğinin ne olduğunu bilmeniz gerekir; geçerli bir kanıt sağlamak için bir ifadede parantezleri yeniden düzenleme kurallarını sağlar. Bu, parantezin yeniden düzenlenmesinin ana denklemle aynı değeri vermesi gerektiği anlamına gelir. Operatörleri değiştirmek için geçerli bir kural sağlar.

İki veya daha fazla operatör içeren bir ifadede, işlenenlerin sırası değiştirilmedikçe gerçekleştirilen işlem önemli değildir. İfade parantez içinde ve içinde yazıyorsa, konumun değiştirilmesi değeri değiştirmez.

Hint-Avrupa dillerinde ifadeler soldan sağa okunduğundan, çoğu infix operatörleri soldan ilişkilendirmelidir; operatörler aynı öncelikte değerlendirilir. Güçte yükselme, infix operatörlerini dikkate alırken kullanılan kuraldır. Önek operatörleri genellikle sağ ilişkiseldir ve sonek operatörleri sol ilişkiseldir.

Bazı dillerde, işleçlere ve işlenenlere eşit değer verilir, burada İlişkilendirmenin bu dil dizisini açık hale getirmesi düşünülmez. Bazı dillerde operatörler ilişkisel olmasa da, bu, parantez kullanımı için karmaşık ifadelerin kullanımını gerekli kılar ve bu da programcılar için karmaşıklığı artırır.

Veri Yapısında Öncelik

Öncelik Sırası, operatörlerin bir ifade ifadesinde izlemesi gereken sıra anlamına gelir. Bu, Infix Notation ile çalışırken yaygın olarak kullanılır.

İki operatör arasında <operatör> <işlenen> <operatör> işleneni durumunda, operatörün atanması tercihi oldukça zordur . Bu nedenle, hesaplama için operatör Öncelik kuralları izlenir. Örneğin, Burada çarpma işlemi daha yüksek önceliğe sahiptir ve daha sonra toplama işlemi gerçekleştirilir.

• En yaygın ancak çok açık olmayan kural, çarpma ve bölme işleminin toplama ve çıkarma işleminden önce yapılması gerektiğidir. Tipik olarak aynı şekilde toplanırlar, bu nedenle tüm operatörler için eşit önem sağlanır.
• Bu işleme mantıksal bir formatta bakıldığında “ve” ve “veya”da varyasyon görülür. Birçok dil, “veya” işlemine daha yüksek Öncelik verildiğinde eşit önem sağlar. Bazı diller, çoğu dilin en yüksek Önceliğe sahip aritmetik işlemler sağladığı çarpma veya “&”, “&” toplamayı “veya” eşit Önceliği dikkate alır.
• Aşırı yükleme, Öncelik'in uygun şekilde tahsis edilmemesi nedeniyle oluşur. Birçok dil, vektör cebir ifadelerinden daha yüksek olumsuzlama (doğru/yanlış) sağlarken, bazıları eşit Öncelik sağlar.

Ayrıca Okuyun: Veri Yapısı Proje Fikirleri

Notasyon Türleri

Şimdi operatör pozisyonunun Notasyon tipine nasıl karar verdiğini öğrenelim.

1. Infix Notasyonu

Infix Notation'da operatörler işlenenler arasında kullanılır. Bir ifadeyi okurken Infix Notation insanlar için oldukça kolaydır. Ancak konu bir bilgisayar algoritması olduğunda, bir infix argümanını işlemek oldukça zaman ve alan gerektirir. Örn: p + q

<işlenenler> <işlemciler> <işlenenler>

Infix Notation, değerlendirmeyi gerçekleştirmek için ek bilgilere ihtiyaç duyar; kurallar, kuralları geçersiz kılmak için İlişkilendirme , Örneğin: p * ( q + r ) / s

• Çağrışım kuralları, ifadenin soldan sağa doğru yapılması gerektiğini, öyle ki p ile çarpmanın q'nun bölünmesinden önce yapılmasını önerir.
• Benzer şekilde, Öncelik kuralları, çarpma ve bölme işleminin toplama ve çıkarma işlemi yapılmadan önce yapılmasını önerir.

2. Önek Gösterimi

Burada önce operatör, ardından bir işlenen yazılır. Lehçe Notasyonu olarak da adlandırılır. Ör. +pq

<işlemciler> <işlenenler> <işlenenler>

Örn: p * ( q + r ) / s

Değerlendirmenin soldan sağa yapılması gerekir ve parantezler denklem modelini değiştirmez veya değiştirmez. Burada “+” konumu “*” nin solunda kaldığı için çarpma işleminden önce toplama işleminin tamamlanması gerekir.

Burada her operatör, hemen solundaki değerler üzerinde işlemler gerçekleştirir. Örneğin, yukarıdaki “+”, “q” ve “r”yi kullanır. Bunu açıklığa kavuşturmak için parantezleri özetleyebiliriz:

((p (qr +) *) s /)

Böylece, “( )”, “p”den hemen sonra gelen iki değeri ve + sonucunu dikkate alır ve kullanır. Benzer şekilde, “/” çarpma ifadesinin sonucunu ve “s”yi kullanır.

3. Postfix Notasyonu

Postfix Notasyonu, öncelikle işlenen, ardından bir operatör tarafından yazılır. Ters Lehçe Notasyonu olarak da adlandırılır, örn., pq+

<işlenenler> <işlenenler> <işlemciler>

Postfix'e gelince, ifadenin Prefix işleminin aynısı soldan sağadır ve “( )” gereksizdir. Burada operatörler sağdan en yakın iki değer üzerinde işlem yapar. Aşağıdaki örnekte, değerlendirme üzerinde herhangi bir etkisi olmadığını belirtmek için gereksiz yere parantezler eklenmiştir.

(/ (* p (+ qr) ) s)

Burada “operatör değerlendirmesi soldan sağa” işlem değerleri sağdadır ve eğer değerlerin kendisi hesaplama içeriyorsa, değerlendirme sırasında bir değişiklik vardır. Yukarıda listelenen örneği alarak, soldaki birincil operatörün “/” olduğuna bakın.

Çarpma işlemi tamamlanana kadar bekler. Ve öncelikle çarpma işleminin bölme hesaplaması başlamadan önce yapılması gerekir (ve yukarıdaki örnekten de çarpma işleminden önce toplama işleminin tamamlanması gerektiği açıktır).

Postfix Notation operatörleri sağındaki değeri kullandığından; hesaplamaları içeren herhangi bir değer, sola doğru hareket ettikçe hesaplamayı zaten tamamlamış olacaktır. Dolayısıyla, ifade hesaplamasının Önek operatörü işlemiyle aynı olmadığı sonucuna varabiliriz.

Üç Notasyonu da vurgulamak için işlenenler aynı sırada gelir ve hesaplama sırasında doğru anlamı sağlamak için operatörlerin hareket ettirilmesi gerekir. Bu, özellikle pq'nin aynı değere sahip olmadıkça her zaman qr olduğunu açıklığa kavuşturmak için “-” ve “/” asimetrik operatörleri düşünüldüğünde dikkate alınmalıdır; değerler “pq -” veya “- pq” ile eşdeğerdir

P+q ≡ +pq ≡ pq+

Örneğin:

Infix- p * q + r / s

Önek – pq * rs / +

Düzeltme sonrası – + * pq / rs

İlk olarak, işlemi gerçekleştirmek için p ve q'yu çarpın ve daha sonra r'yi s'ye bölün ve en sonunda sonuçları toplayın.

Üç Notasyon arasındaki tablo özetlerinin altında,

Infix Notasyonu	Lehçe Notasyonu	Ters cila gösterimi
p+q	+pq	pq+
(p+q)*r	+*pq	pqr+*
p*(q+r)	*p+qr	pqr*+ +
p÷q+r÷s	+÷pq÷rs	pq÷rs÷+
(pq)*(rs)	*-pq-rs	pq-rs-*

Gösterimler Arası Dönüşüm

*Açık bir içgörü sağlamak için ifadeye parantezler eklenmiştir,

Infix	son düzeltme	Önek
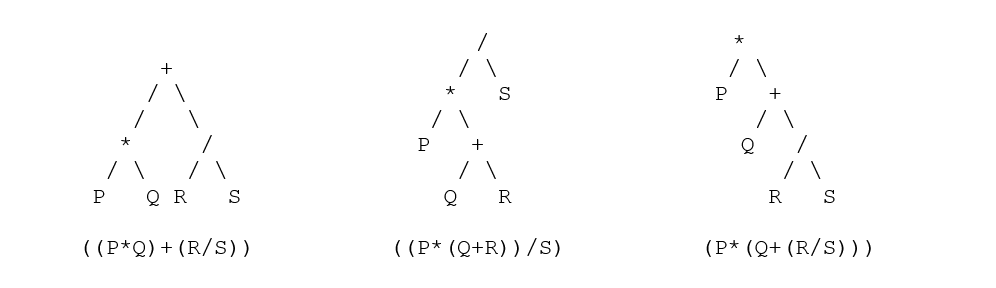
( (p * q) + (r / s) )	( (pq *) (rs /) +)	(+ (* pq) (/ rs))
((p * (q + r)) ) / s)	( (p (qr +) *) s /)	(/ (* p (+ qr) ) s)
(p * (q + (r / s)) )	(p (q (rs /) +) *)	(* p (+ q (/ rs)) )

• Parantez içindeki operatörler tarafından doğrudan parantez içine alınmış formlarda dönüştürmeye başlayabilirsiniz, örneğin (m + n) veya (mn +) veya (+ mn). Şimdi istenmeyen parantezleri kaldırarak bunu tüm operatörlerde tekrarlayın.
• Şimdi ağaçları dönüştürmek ve ayrıştırmak için yukarıda gösterilen bu numarayı kullanın – her düğüm için eşdeğer ayrıştırma ağaçları:

Ödeme: Python'da Veri Yapısı ve Algoritma

Çözüm

Veri Yapısında İfade Ayrıştırma , Infix, Postfix ve Prefix Aritmetik ifadelerdeki gösterimler oldukça farklıdır ancak ifade yazma yöntemleri aynıdır. Bunları bilmek program yazarken çok önemlidir.

Bir bilgisayar programlama dilinde, ifade dikkate alınır ve dizeden ayrıştırılır. İlişkilendirme ve Öncelik kuralı farklı dillerde oldukça değişir.

Neden upGrad ile bir Veri bilimi kursu seçmelisiniz?

Veri bilimi, bilgisayar biliminde gelişen alanlardan biridir. Şirketler, kodlama dilinden bağımsız olarak programlama için temel olan temel bilgiler hakkında iyi bilgiye sahip programcılara ihtiyaç duyar.

upGrad, veri bilimcisi olmak için her temel ihtiyacı kapsayan, anlayışlı ve bilgilendirici sınıflar sağlamaya odaklanır. upGrad'ın Veri Biliminde 12 Aylık Yönetici PG Programı. IIIT Bangalore tarafından sunulan , Hindistan'ın 1. NASSCOM sertifikalı kursu olup, Veri Bilimi Endüstrisi Uzmanlarından 1:1 kişiselleştirilmiş rehberlikle birlikte tüm temel Programlama Dillerini, Araçları ve Kitaplıkları kapsar. Yüksek ücretli veri bilimi işinize başlamanız için size en iyi temeli sağlar.

Veri Yapıları nedir?

Veri yapıları, bellekteki verileri düzenlemek için kullanılır. Diziler, listeler, yığınlar, kuyruklar ve diğerleri dahil olmak üzere bellekte veri düzenlemek için çeşitli yöntemler vardır. Veri yapısı, C, C++ veya Java gibi bir programlama dili değildir. Bunun yerine, herhangi bir programlama dilinde bellekteki verileri düzenlemek için kullanılan bir dizi tekniktir. Bir veri yapısı, verileri verimli bir şekilde organize etme, işleme ve saklama yöntemidir. Veri öğeleri, veri yapısının yardımıyla basitçe geçilebilir. Programın ana işi, kullanıcının verilerini mümkün olan en kısa sürede kaydetmek ve almak olduğundan, bir programın hızını arttırmada çok önemlidir.

Veri ayrıştırmanın gerçek hayattaki kullanımları nelerdir?

Verileri bir biçimden diğerine dönüştürme işlemi, veri ayrıştırma olarak bilinir. Bilgisayar kodunu ayrıştırmak ve makine kodu oluşturmak için derleyicilerde yaygın olarak kullanılırlar. Verileri bir biçimden diğerine dönüştürme işlemi, veri ayrıştırma olarak bilinir. Aldığımız ham HTML'yi anlamak zor olduğundan, ayrıştırıcılar genellikle çevrimiçi kazımada kullanılır. Verilerin insan tarafından okunabilir bir biçime dönüştürülmesini istiyoruz. Bu, en alakalı bilgileri sağlamak için HTML dizeleri veya tabloları kullanarak raporlar oluşturma anlamına gelebilir.

İlişkilendirme ve Öncelik, veri yapılandırmasında nasıl yardımcı olur?

İfadelerin değerlendirme sırası, operatörlerin iki özelliği tarafından belirlenir: öncelik ve ilişkilendirilebilirlik. Öncelik, bir ifadedeki terimlerin nasıl gruplandırılması ve bir ifadenin nasıl değerlendirilmesi gerektiğini belirlemeye yardımcı olur. Çoğu ifade BODMAS çerçevesini kullandığından, belirli operatörler diğerlerine göre önceliklidir. Bir ifadede iki operatör aynı önceliğe sahip olduğunda, birlik kuralı uygulanır. Derleyicinin tercihine göre, ilişkilendirme soldan sağa veya sağdan sola olabilir.