Basit Örneklerle Bayes Karar Teorisini Anlamak

Tanıtım

Gerçek hayatta birçok sınıflandırma problemi ile karşılaşmaktayız. Örneğin, bir elektronik mağazanın belirli bir müşterinin belirli bir yaşa göre bilgisayar alıp almayacağını bilmesi gerekebilir. Bu makale ile, belirli bir özelliğe dayalı olarak 'x' olasılığı olan bir sınıfı mı yoksa 'y' olasılığı olan bir karşı sınıfı mı seçeceğimize karar vermemize yardımcı olan 'Bayesian Decision Theory' adlı bir yöntemi tanıtacağız.

Tanım

Bayesian Karar Teorisi , örüntü sınıflandırması gibi çeşitli problemlere basit ama temel bir yaklaşımdır. Bayes Karar Teorisinin tüm amacı, bize en az 'risk'e mal olacak kararları seçmemize yardımcı olmaktır. Seçtiğimiz herhangi bir karara bağlı olarak her zaman bir tür risk vardır. Bu sınıflandırmanın içerdiği riskleri bu makalenin ilerleyen kısımlarında inceleyeceğiz.

Temel Karar

Bir elektronik mağazası şirketinin, bir müşterinin bilgisayar alıp almayacağını öğrenmek istediği bir örneği ele alalım. Yani aşağıdaki iki satın alma sınıfımız var:

w1 – Evet (Müşteri bir bilgisayar alacak)

w2 – Hayır (Müşteri bilgisayar almayacak)

Şimdi, müşteri veri tabanımızın geçmiş kayıtlarına bakacağız. Bilgisayar alan müşteri sayısını ve bilgisayar almayan müşteri sayısını not edeceğiz. Şimdi müşterilerin bilgisayar satın alma olasılıklarını hesaplayacağız. P(w1) olsun. Benzer şekilde, müşterilerin bir müşteriyi satın almama olasılığı P(w2)'dir.

Şimdi gelecekteki müşterilerimiz için temel bir karşılaştırma yapacağız.

Yeni bir müşteri için,

P(w1) > P(w2) ise, müşteri bir bilgisayar (w1) satın alacaktır.

Ve eğer P(w2) > P(w1) ise, müşteri bir bilgisayar (w2) satın almayacak.

Burada karar problemimizi çözdük.

Ancak, bu temel Karar yöntemiyle ilgili sorun nedir? Pek çoğunuz doğru tahmin etmiş olabilirsiniz. Sadece önceki kayıtlara dayanarak, gelecekteki tüm müşteriler için her zaman aynı kararı verecektir. Bu mantıksız ve saçma.

Bu nedenle, gelecekteki müşteriler için daha iyi kararlar vermemize yardımcı olacak bir şeye ihtiyacımız var. Bunu bazı özellikleri tanıtarak yapıyoruz. Diyelim ki, 'x' müşterinin yaşını ifade ettiği bir 'x' özelliği ekleyelim. Artık eklenen bu özellik ile daha iyi kararlar alabileceğiz.

Bunu yapmak için Bayes Teoreminin ne olduğunu bilmemiz gerekiyor.

Okuyun: Denetimli Öğrenme Türleri

Bayes Teoremi ve Karar Teorisi

w1 sınıfımız ve 'x' özelliğimiz için:

P(w1 | x) = P(x | w1) * P(w1) P(x)

Bu formülde anlamamız gereken 4 terim var:

1. Önce – P(w1), veri gözlemlenmeden önce w1'in doğru olduğuna dair Ön Olasılıktır.
2. Arka – P(w1 | x), veri gözlemlendikten sonra w1'in doğru olduğu Arka Olasılıktır.
3. Kanıt – P(x) Verinin Toplam Olasılığıdır
4. Olasılık – P(x | w1) 'x' tarafından sağlanan w1 hakkında bilgidir

P(w1 | x), x verilen w1'in olasılığı olarak okunur

Daha doğrusu, belirli bir müşterinin yaşı göz önüne alındığında, bir müşterinin bir bilgisayar satın alma olasılığıdır.

Artık kararımızı vermeye hazırız:

Yeni bir müşteri için,

P(w1 | x) > P(w2 | x) ise, müşteri bir bilgisayar satın alacaktır (w1)

Ve eğer P(w2 | x) > P(w1 | x) ise, o zaman müşteri bir bilgisayar satın almayacak (w2)

Bu karar daha mantıklı ve güvenilir görünüyor çünkü burada üzerinde çalışmamız gereken bazı özellikler var ve kararımız yeni müşterilerimizin özelliklerine ve ayrıca eski kayıtlara değil, eski kayıtlara değil, geçmiş kayıtlara dayanıyor.

Şimdi, formülden, hem w1 hem de w2 sınıflarımız için paydamızın P(x) sabit olduğunu görebilirsiniz. Böylece, bu fikri kullanabiliriz ve aşağıdaki gibi başka bir karar biçimi oluşturabiliriz:

P(x | w1)*P(w1) > P(x | w2)*P(w2) ise, müşteri bir bilgisayar satın alacaktır (w1)

Ve eğer P(x | w2)*P(w2) > P(x | w1)*P(w1) ise, müşteri bir bilgisayar satın almayacak (w2)

Burada ilginç bir gerçeği fark edebiliriz. Bir şekilde, önceki olasılıklarımız P(w1) ve P(w2) eşitse, kararımızı yine de P(x | w1) ve P(x | w2) olasılık olasılıklarımıza dayanarak verebiliriz. Benzer şekilde, olasılık olasılıklarımız eşitse, önceki P(w1) ve P(w2) olasılıklarımıza dayanarak kararlar verebiliriz.

Mutlaka Okuyun: Makine Öğreniminde Regresyon Modellerinin Türleri

Risk Hesaplama

Daha önce de belirtildiği gibi, kararda her zaman bir miktar 'risk' veya hata olacaktır. Dolayısıyla, bir kararda yapılan hata olasılığını da belirlememiz gerekiyor. Bu çok basit ve bunu görselleştirmeler açısından göstereceğim.

Elimizde bazı veriler olduğunu ve Bayesian Karar Teorisine göre bir karar verdiğimizi düşünelim.

Aşağıdaki gibi bir grafik elde ederiz:

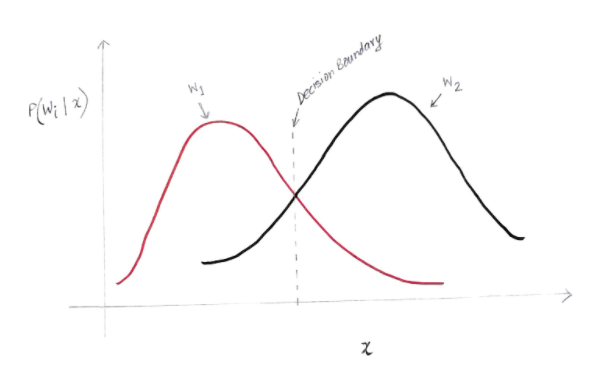
Y ekseni, P(w(i) | x) sonsal olasılığıdır ve x ekseni, 'x' özelliğimizdir. Her iki sınıf için de arka olasılığın eşit olduğu eksene karar sınırımız denir.

Yani Karar Sınırında:

P(w1 | x) = P(w2 | x)

Yani karar sınırının solunda w1(bilgisayar satın alma) lehine karar veriyoruz ve karar sınırının sağında w2(bilgisayar almama) lehine karar veriyoruz.

Ancak, grafikte de görebileceğiniz gibi, karar sınırının solunda w2'nin sıfır olmayan bir büyüklüğü var. Ayrıca, karar sınırının sağında w1'in sıfırdan farklı bir büyüklüğü vardır. Başka bir sınıfın başka bir sınıf üzerindeki bu uzantısı, sizin risk veya olasılık hatası olarak adlandırdığınız şeydir.

Olasılık Hatasının Hesaplanması

w1 sınıfı için hata olasılığını hesaplamak için, karar sınırının solundaki alanda sınıfın w2 olma olasılığını bulmamız gerekir. Benzer şekilde, w2 sınıfı için hata olasılığı, sınıfın karar sınırının sağındaki alanda w1 olma olasılığıdır.

Matematiksel olarak konuşursak, sınıf için minimum hata:

w1, P(w2 | x)

Ve w2 sınıfı için P(w1 | x)

İstediğiniz olasılık hatasını aldınız. Basit, değil mi?

Peki şimdi toplam hata nedir?

Bir x özelliği için toplam hata olasılığını P(E | x) olarak gösterelim. Bir x özelliği için toplam hata, o x özelliği için tüm hata olasılıklarının toplamı olacaktır. Basit entegrasyon kullanarak bunu çözebiliriz ve elde ettiğimiz sonuç:

P(E | x) = minimum (P(w1 | x), P(w2 | x))

Bu nedenle, toplam hata olasılığımız, her iki sınıf için de arka olasılığın minimumudur. Bir sınıfın minimumunu alıyoruz çünkü sonuçta diğer sınıfa göre bir karar vereceğiz.

Çözüm

Bayesian Karar Teorisinin ayrık uygulamalarına ayrıntılı olarak baktık. Artık Bayes Teoremi ve terimlerini biliyorsunuz. Ayrıca karar verirken Bayes Teoremini nasıl uygulayacağınızı da biliyorsunuz. Ayrıca vermiş olduğunuz karardaki hatayı nasıl tespit edeceğinizi de öğrendiniz.

Makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, çalışan profesyoneller için tasarlanmış ve 450+ saat zorlu eğitim, 30'dan fazla vaka çalışması ve ödev, IIIT- sunan IIIT-B & upGrad'ın Makine Öğrenimi ve Yapay Zeka PG Diplomasına göz atın. B Mezun statüsü, 5+ pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.