Понимание байесовской теории принятия решений на простом примере

Введение

В реальной жизни мы сталкиваемся с множеством проблем классификации. Например, магазину электроники может потребоваться знать, собирается ли конкретный покупатель определенного возраста покупать компьютер или нет. В этой статье мы собираемся представить метод под названием «Байесовская теория принятия решений», который помогает нам принимать решения о том, следует ли выбирать класс с вероятностью «x» или противоположный класс с вероятностью «y» на основе определенного признака.

Определение

Байесовская теория принятия решений — это простой, но фундаментальный подход к множеству проблем, таких как классификация образов. Вся цель теории принятия решений Байеса состоит в том, чтобы помочь нам выбрать решения, которые будут стоить нам наименьшего «риска». Любое решение, которое мы принимаем, всегда сопряжено с определенным риском. Далее в этой статье мы рассмотрим риски, связанные с этой классификацией.

Основное решение

Давайте возьмем пример, когда компания магазина электроники хочет знать, собирается ли покупатель покупать компьютер или нет. Итак, у нас есть следующие два класса покупки:

w1 – Да (Клиент купит компьютер)

w2 – Нет (Клиент не будет покупать компьютер)

Теперь мы рассмотрим прошлые записи нашей базы данных клиентов. Мы запишем количество клиентов, покупающих компьютеры, а также количество клиентов, не покупающих компьютер. Теперь посчитаем вероятности покупателей, купивших компьютер. Пусть это будет P(w1). Точно так же вероятность того, что клиенты не купят клиента, равна P(w2).

Теперь мы сделаем базовое сравнение для наших будущих клиентов.

Для нового клиента,

Если P(w1) > P(w2), то клиент купит компьютер (w1)

А если P(w2) > P(w1), то клиент не будет покупать компьютер (w2)

Здесь мы решили нашу проблему принятия решений.

Но в чем проблема с этим основным методом принятия решений? Что ж, большинство из вас, возможно, догадались правильно. Основываясь только на предыдущих записях, он всегда будет давать одно и то же решение для всех будущих клиентов. Это нелогично и абсурдно.

Поэтому нам нужно что-то, что поможет нам принимать лучшие решения для будущих клиентов. Мы делаем это, вводя некоторые функции. Допустим, мы добавляем функцию «x», где «x» обозначает возраст клиента. Теперь с этой добавленной функцией мы сможем принимать лучшие решения.

Для этого нам нужно знать, что такое теорема Байеса.

Читайте: Типы контролируемого обучения

Теорема Байеса и теория принятия решений

Для нашего класса w1 и функции «x» мы имеем:

P(w1 | x) = P(x | w1) * P(w1) P(x)

В этой формуле есть 4 термина, которые нам нужно понять:

1. Априорная - P (w1) - это априорная вероятность того, что w1 верно до того, как данные будут наблюдаться.
2. Апостериорная — P(w1 | x) — это апостериорная вероятность того, что w1 истинно после наблюдения данных.
3. Доказательство - P (x) - это общая вероятность данных.
4. Вероятность - P (x | w1) - это информация о w1, предоставленная «x»

P(w1 | x) читается как Вероятность w1 при заданном x

Точнее, это вероятность того, что клиент купит компьютер, учитывая его возраст.

Теперь мы готовы принять решение:

Для нового клиента,

Если P(w1 | x) > P(w2 | x), то клиент купит компьютер (w1)

И если P(w2 | x) > P(w1 | x), то клиент не будет покупать компьютер (w2)

Это решение кажется более логичным и заслуживающим доверия, поскольку у нас есть некоторые особенности, над которыми нужно работать, и наше решение основано на характеристиках наших новых клиентов, а также на прошлых записях, а не только в прошлых записях, как в более ранних случаях.

Теперь из формулы видно, что для обоих наших классов w1 и w2 наш знаменатель P(x) постоянен. Итак, мы можем использовать эту идею и сформировать другую форму решения, как показано ниже:

Если P(x | w1)*P(w1) > P(x | w2)*P(w2), то клиент купит компьютер (w1)

И если P(x | w2)*P(w2) > P(x | w1)*P(w1), то клиент не будет покупать компьютер (w2)

Здесь мы можем отметить интересный факт. Если каким-то образом наши априорные вероятности P(w1) и P(w2) равны, мы все равно можем принять решение на основе наших вероятностей правдоподобия P(x | w1) и P(x | w2). Точно так же, если наши вероятности правдоподобия равны, мы можем принимать решения на основе наших априорных вероятностей P(w1) и P(w2).

Обязательно прочтите: Типы регрессионных моделей в машинном обучении

Расчет риска

Как упоминалось ранее, всегда будет некоторый «риск» или ошибка в решении. Итак, нам также необходимо определить вероятность ошибки, сделанной в решении. Это очень просто, и я продемонстрирую это с точки зрения визуализации.

Предположим, что у нас есть некоторые данные, и мы приняли решение в соответствии с байесовской теорией принятия решений.

Мы получаем график примерно такой, как показано ниже:

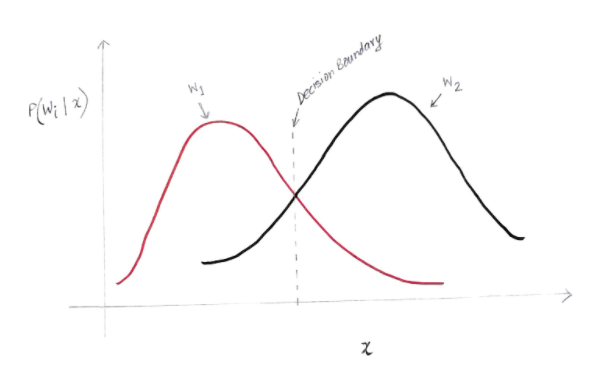
Ось Y — это апостериорная вероятность P (w (i) | x), а ось X — это наша функция «x». Ось, на которой апостериорная вероятность для обоих классов равна, называется границей нашего решения.

Итак, на границе решения:

P(w1 | x) = P(w2 | x)

Таким образом, слева от границы решения мы принимаем решение в пользу w1 (покупка компьютера), а справа от границы решения мы решаем в пользу w2 (не покупать компьютер).

Но, как вы можете видеть на графике, слева от границы решения есть некоторая ненулевая величина w2. Кроме того, справа от границы решения имеется некоторая ненулевая величина w1. Это расширение другого класса над другим классом и есть то, что вы называете ошибкой риска или вероятности.

Расчет вероятности ошибки

Чтобы вычислить вероятность ошибки для класса w1, нам нужно найти вероятность того, что класс w2 находится в области, которая находится слева от границы решения. Точно так же вероятность ошибки для класса w2 — это вероятность того, что класс w1 находится в области, которая находится справа от границы решения.

С математической точки зрения минимальная ошибка для класса:

w1 есть P(w2 | x)

А для класса w2 есть P(w1 | x)

Вы получили желаемую ошибку вероятности. Просто, не так ли?

Итак, какова общая ошибка сейчас?

Обозначим вероятность полной ошибки признака x как P(E | x). Общая ошибка для функции x будет суммой всех вероятностей ошибки для этой функции x. Используя простую интеграцию, мы можем решить это, и в результате мы получим:

P(E | x) = минимум (P(w1 | x), P(w2 | x))

Следовательно, наша вероятность полной ошибки является минимумом апостериорной вероятности для обоих классов. Мы берем минимум класса, потому что в конечном итоге мы дадим решение, основанное на другом классе.

Заключение

Мы подробно рассмотрели дискретные приложения байесовской теории принятия решений. Теперь вы знаете теорему Байеса и ее условия. Вы также знаете, как применять теорему Байеса при принятии решения. Вы также научились определять ошибку в принятом вами решении.

Если вам интересно узнать больше о машинном обучении, ознакомьтесь с дипломом PG IIIT-B и upGrad в области машинного обучения и искусственного интеллекта, который предназначен для работающих профессионалов и предлагает более 450 часов тщательного обучения, более 30 тематических исследований и заданий, IIIT- Статус B Alumni, более 5 практических практических проектов и помощь в трудоустройстве в ведущих фирмах.