Înțelegerea teoriei deciziei bayesiene cu un exemplu simplu

Introducere

Întâmpinăm o mulțime de probleme de clasificare în viața reală. De exemplu, un magazin de electronice ar putea avea nevoie să știe dacă un anumit client, în funcție de o anumită vârstă, va cumpăra sau nu un computer. Prin acest articol, vom introduce o metodă numită „Teoria Bayesiană a Deciziei” care ne ajută să luăm decizii cu privire la alegerea unei clase cu probabilitate „x” sau o clasă opusă cu probabilitate „y” pe baza unei anumite caracteristici.

Definiție

Teoria Bayesiană a Deciziei este o abordare simplă, dar fundamentală, pentru o varietate de probleme, cum ar fi clasificarea modelelor. Întregul scop al teoriei deciziei Bayes este să ne ajute să alegem deciziile care ne vor costa cel mai puțin „risc”. Există întotdeauna un fel de risc legat de orice decizie pe care o alegem. Vom trece prin riscul implicat în această clasificare mai târziu în acest articol.

Decizie de bază

Să luăm un exemplu în care o companie de magazin de electronice dorește să știe dacă un client va cumpăra sau nu un computer. Deci avem următoarele două clase de cumpărare:

w1 – Da (clientul va cumpăra un computer)

w2 – Nu (clientul nu va cumpăra un computer)

Acum, vom analiza înregistrările anterioare ale bazei noastre de clienți. Vom nota numărul de clienți care cumpără computere și, de asemenea, numărul de clienți care nu cumpără un computer. Acum, vom calcula probabilitățile clienților să cumpere un computer. Fie P(w1). În mod similar, probabilitatea ca clienții să nu cumpere un client este P(w2).

Acum vom face o comparație de bază pentru viitorii noștri clienți.

Pentru un client nou,

Dacă P(w1) > P(w2), atunci clientul va cumpăra un computer (w1)

Și, dacă P(w2) > P(w1), atunci clientul nu va cumpăra un computer (w2)

Aici, ne-am rezolvat problema de decizie.

Dar, care este problema cu această metodă de decizie de bază? Ei bine, majoritatea dintre voi s-ar putea să fi ghicit bine. Pe baza doar înregistrărilor anterioare, va da întotdeauna aceeași decizie pentru toți viitorii clienți. Acest lucru este ilogic și absurd.

Deci avem nevoie de ceva care să ne ajute să luăm decizii mai bune pentru viitorii clienți. Facem asta prin introducerea unor caracteristici. Să presupunem că adăugăm o caracteristică „x” unde „x” indică vârsta clientului. Acum, cu această funcție adăugată, vom putea lua decizii mai bune.

Pentru a face acest lucru, trebuie să știm ce este teorema Bayes.

Citiți: Tipuri de învățare supravegheată

Teorema Bayes și teoria deciziei

Pentru clasa noastră w1 și caracteristica „x”, avem:

P(w1 | x) = P(x | w1) * P(w1) P(x)

Există 4 termeni în această formulă pe care trebuie să îi înțelegem:

1. Anterior – P(w1) este Probabilitatea Prioră ca w1 să fie adevărat înainte ca datele să fie observate
2. Posterior – P(w1 | x) este Probabilitatea Posterior ca w1 să fie adevărată după observarea datelor.
3. Dovezi – P(x) este probabilitatea totală a datelor
4. Probabilitate – P(x | w1) este informația despre w1 furnizată de „x”

P(w1 | x) se citește ca Probabilitatea w1 dat x

Mai exact, este probabilitatea ca un client să cumpere un computer, având în vedere vârsta unui anumit client.

Acum suntem gata să luăm decizia noastră:

Pentru un client nou,

Dacă P(w1 | x) > P(w2 | x), atunci clientul va cumpăra un computer (w1)

Și, dacă P(w2 | x) > P(w1 | x), atunci clientul nu va cumpăra un computer (w2)

Această decizie pare mai logică și mai demnă de încredere, deoarece avem câteva caracteristici la care să lucrăm și decizia noastră se bazează pe caracteristicile noilor noștri clienți și, de asemenea, pe înregistrările anterioare și nu doar pe înregistrările anterioare, ca în cazurile anterioare.

Acum, din formulă, puteți vedea că pentru ambele clasele noastre w1 și w2, numitorul nostru P(x) este constant. Deci, putem folosi această idee și putem forma o altă formă de decizie, după cum urmează:

Dacă P(x | w1)*P(w1) > P(x | w2)*P(w2), atunci clientul va cumpăra un computer (w1)

Și, dacă P(x | w2)*P(w2) > P(x | w1)*P(w1), atunci clientul nu va cumpăra un computer (w2)

Putem observa aici un fapt interesant. Dacă cumva, probabilitățile noastre anterioare P(w1) și P(w2) sunt egale, putem totuși să ne putem lua decizia pe baza probabilităților noastre de probabilitate P(x | w1) și P(x | w2). În mod similar, dacă probabilitățile noastre de probabilitate sunt egale, putem lua decizii pe baza probabilităților noastre anterioare P(w1) și P(w2).

Trebuie citit: Tipuri de modele de regresie în învățarea automată

Calculul riscului

După cum am menționat mai devreme, va exista întotdeauna o anumită cantitate de „risc” sau eroare făcută în decizie. Deci, trebuie să determinăm și probabilitatea de eroare făcută într-o decizie. Acest lucru este foarte simplu și voi demonstra asta în ceea ce privește vizualizările.

Să considerăm că avem câteva date și am luat o decizie conform teoriei deciziilor bayesiene.

Obținem un grafic oarecum ca mai jos:

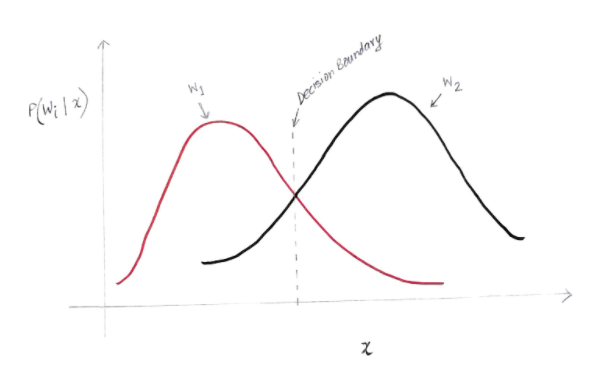
Axa y este probabilitatea posterioară P(w(i) | x) iar axa x este caracteristica noastră „x”. Axa în care probabilitatea posterioară pentru ambele clase este egală, acea axă se numește granița noastră de decizie.

Deci, la limita de decizie:

P(w1 | x) = P(w2 | x)

Deci, în stânga graniței de decizie, decidem în favoarea w1 (cumpărarea unui computer), iar în dreapta graniței de decizie, decidem în favoarea w2 (nu cumpărarea unui computer).

Dar, după cum puteți vedea în grafic, există o magnitudine diferită de zero a lui w2 la stânga graniței de decizie. De asemenea, există o magnitudine diferită de zero a lui w1 la dreapta graniței de decizie. Această extindere a unei alte clase peste o altă clasă este ceea ce numiți eroare de risc sau probabilitate.

Calculul erorii de probabilitate

Pentru a calcula probabilitatea de eroare pentru clasa w1, trebuie să găsim probabilitatea ca clasa să fie w2 în zona care se află la stânga limitei de decizie. În mod similar, probabilitatea de eroare pentru clasa w2 este probabilitatea ca clasa să fie w1 în zona care se află la dreapta graniței de decizie.

Matematic vorbind, eroarea minimă pentru clasă:

w1 este P(w2 | x)

Și pentru clasa w2 este P(w1 | x)

Ai primit eroarea de probabilitate dorită. Simplu, nu-i așa?

Deci, care este eroarea totală acum?

Să notăm probabilitatea de eroare totală pentru o caracteristică x să fie P(E | x). Eroarea totală pentru o caracteristică x ar fi suma tuturor probabilităților de eroare pentru acea caracteristică x. Folosind o integrare simplă, putem rezolva acest lucru și rezultatul pe care îl obținem este:

P(E | x) = minim (P(w1 | x) , P(w2 | x))

Prin urmare, probabilitatea noastră de eroare totală este minimul probabilității posterioare pentru ambele clase. Luăm minimul unei clase pentru că în cele din urmă vom da o decizie în funcție de cealaltă clasă.

Concluzie

Am analizat în detaliu aplicațiile discrete ale teoriei deciziilor bayesiene. Acum cunoașteți teorema Bayes și termenii ei. De asemenea, știți cum să aplicați teorema Bayes în luarea unei decizii. De asemenea, ați învățat cum să determinați eroarea din decizia pe care ați luat-o.

Dacă sunteți interesat să aflați mai multe despre învățarea automată, consultați Diploma PG de la IIIT-B și upGrad în Învățare automată și AI, care este concepută pentru profesioniști care lucrează și oferă peste 450 de ore de pregătire riguroasă, peste 30 de studii de caz și sarcini, IIIT- B Statut de absolvenți, peste 5 proiecte practice practice și asistență pentru locuri de muncă cu firme de top.