用簡單的例子理解貝葉斯決策理論

介紹

我們在現實生活中會遇到很多分類問題。 例如，一家電子商店可能需要知道基於特定年齡的特定客戶是否會購買計算機。 通過這篇文章，我們將介紹一種名為“貝葉斯決策理論”的方法，它可以幫助我們根據某個特徵來決定是選擇具有“x”概率的類還是選擇具有“y”概率的相反類。

定義

貝葉斯決策理論是解決模式分類等各種問題的簡單但基本的方法。 貝葉斯決策理論的全部目的是幫助我們選擇成本最低“風險”的決策。 我們選擇的任何決定總是存在某種風險。 我們將在本文後面介紹此分類所涉及的風險。

基本決定

讓我們舉一個例子，一家電子商店公司想知道客戶是否要購買電腦。 所以我們有以下兩個購買等級：

w1 - 是（客戶將購買計算機）

w2 – 否（客戶不會購買計算機）

現在，我們將查看客戶數據庫的過去記錄。 我們會記下購買電腦的客戶數量以及不購買電腦的客戶數量。 現在，我們將計算客戶購買計算機的概率。 讓它成為 P(w1)。 類似地，客戶不購買客戶的概率為 P(w2)。

現在我們將為我們未來的客戶做一個基本的比較。

對於一個新客戶，

如果 P(w1) > P(w2)，那麼客戶將購買一台計算機 (w1)

並且，如果 P(w2) > P(w1)，則客戶不會購買計算機 (w2)

在這裡，我們已經解決了我們的決策問題。

但是，這種基本的決策方法有什麼問題？ 好吧，你們中的大多數人可能都猜對了。 僅基於以前的記錄，它將始終為所有未來的客戶做出相同的決定。 這是不合邏輯和荒謬的。

因此，我們需要一些能夠幫助我們為未來客戶做出更好決策的東西。 我們通過引入一些功能來做到這一點。 假設我們添加了一個特徵“x”，其中“x”表示客戶的年齡。 現在有了這個附加功能，我們將能夠做出更好的決定。

為此，我們需要知道貝葉斯定理是什麼。

閱讀：監督學習的類型

貝葉斯定理和決策理論

對於我們的類 w1 和特徵“x”，我們有：

P(w1 | x) = P(x | w1) * P(w1) P(x)

這個公式中有4個術語需要我們理解：

1. Prior – P(w1) 是在觀察數據之前 w1 為真的先驗概率
2. 後驗 – P(w1 | x) 是觀察數據後 w1 為真的後驗概率。
3. 證據 – P(x) 是數據的總概率
4. 似然性——P(x | w1) 是“x”提供的關於 w1 的信息

P(w1 | x) 讀作 w1 給定 x 的概率

更準確地說，它是給定特定客戶年齡的客戶購買計算機的概率。

現在，我們準備好做出決定了：

對於一個新客戶，

如果 P(w1 | x) > P(w2 | x)，那麼客戶將購買一台計算機 (w1)

並且，如果 P(w2 | x) > P(w1 | x)，那麼客戶不會購買計算機 (w2)

這個決定似乎更合乎邏輯和值得信賴，因為我們在這裡有一些功能需要處理，而且我們的決定是基於我們新客戶的特徵以及過去的記錄，而不是像以前的案例那樣只是過去的記錄。

現在，從公式中，您可以看到對於我們的類 w1 和 w2，我們的分母 P(x) 是恆定的。 因此，我們可以利用這個想法，形成另一種形式的決策，如下所示：

如果 P(x | w1)*P(w1) > P(x | w2)*P(w2)，那麼客戶將購買一台計算機 (w1)

並且，如果 P(x | w2)*P(w2) > P(x | w1)*P(w1)，則客戶不會購買計算機 (w2)

我們可以在這裡註意到一個有趣的事實。 如果不知何故，我們的先驗概率 P(w1) 和 P(w2) 相等，我們仍然可以根據我們的似然概率 P(x | w1) 和 P(x | w2) 做出決定。 類似地，如果我們的似然概率相等，我們可以根據我們的先驗概率 P(w1) 和 P(w2) 做出決定。

必讀：機器學習中的回歸模型類型

風險計算

如前所述，決策中總會存在一定程度的“風險”或錯誤。 因此，我們還需要確定決策中出錯的概率。 這非常簡單，我將在可視化方面進行演示。

讓我們考慮一下我們有一些數據，並且我們已經根據貝葉斯決策理論做出了決定。

我們得到一個有點像下面的圖表：

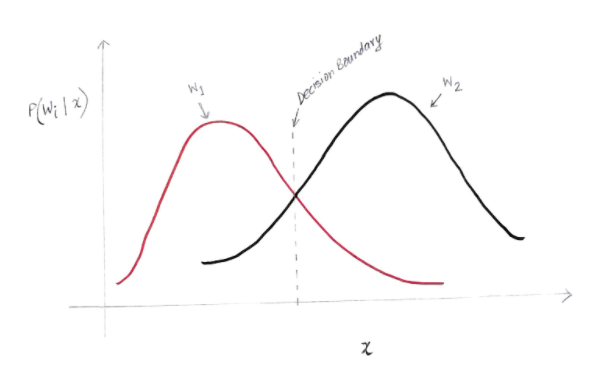
y 軸是後驗概率 P(w(i) | x)，x 軸是我們的特徵“x”。 兩個類的後驗概率相等的軸稱為我們的決策邊界。

所以在決策邊界：

P(w1 | x) = P(w2 | x)

因此，在決策邊界的左側，我們決定支持 w1（購買計算機），而在決策邊界的右側，我們決定支持 w2（不購買計算機）。

但是，正如您在圖中看到的那樣，在決策邊界的左側有一些 w2 的非零幅度。 此外，在決策邊界的右側有一些 w1 的非零幅度。 另一個類對另一個類的這種擴展就是你所說的風險或概率錯誤。

概率誤差的計算

為了計算類別 w1 的錯誤概率，我們需要在決策邊界左側的區域中找到類別為 w2 的概率。 類似地，類 w2 的錯誤概率是該類在決策邊界右側的區域中為 w1 的概率。

從數學上講，類的最小誤差：

w1 是 P(w2 | x)

對於 w2 類是 P(w1 | x)

你得到了你想要的概率錯誤。 很簡單，不是嗎？

那麼現在的總誤差是多少？

讓我們將特徵 x 的總錯誤概率表示為 P(E | x)。 特徵 x 的總誤差將是該特徵 x 的所有錯誤概率的總和。 使用簡單的集成，我們可以解決這個問題，我們得到的結果是：

P(E | x) = 最小值 (P(w1 | x) , P(w2 | x))

因此，我們的總錯誤概率是兩個類的後驗概率的最小值。 我們選擇一個班級的最小值，因為最終我們將根據另一個班級做出決定。

結論

我們已經詳細研究了貝葉斯決策理論的離散應用。 您現在知道貝葉斯定理及其術語。 您還知道如何在決策中應用貝葉斯定理。 您還學習瞭如何確定您做出的決定中的錯誤。

如果您有興趣了解有關機器學習的更多信息，請查看 IIIT-B 和 upGrad 的機器學習和人工智能 PG 文憑，該文憑專為工作專業人士設計，提供 450 多個小時的嚴格培訓、30 多個案例研究和作業、IIIT- B 校友身份、5 個以上實用的實踐頂點項目和頂級公司的工作協助。