Entendendo a Teoria da Decisão Bayesiana com Exemplo Simples

Introdução

Encontramos muitos problemas de classificação na vida real. Por exemplo, uma loja de eletrônicos pode precisar saber se um determinado cliente com base em uma certa idade vai comprar um computador ou não. Através deste artigo, vamos introduzir um método chamado 'Teoria da Decisão Bayesiana' que nos ajuda a tomar decisões sobre selecionar uma classe com probabilidade 'x' ou uma classe oposta com probabilidade 'y' com base em uma determinada característica.

Definição

A Teoria da Decisão Bayesiana é uma abordagem simples, mas fundamental para uma variedade de problemas como classificação de padrões. Todo o propósito da Teoria da Decisão de Bayes é nos ajudar a selecionar decisões que nos custem o menor 'risco'. Há sempre algum tipo de risco associado a qualquer decisão que escolhemos. Estaremos analisando o risco envolvido nessa classificação mais adiante neste artigo.

Decisão Básica

Tomemos um exemplo em que uma empresa de loja de eletrônicos deseja saber se um cliente vai comprar um computador ou não. Assim, temos as duas classes de compra a seguir:

w1 – Sim (Cliente comprará um computador)

w2 – Não (Cliente não comprará computador)

Agora, examinaremos os registros anteriores de nosso banco de dados de clientes. Vamos anotar o número de clientes que compram computadores e também o número de clientes que não compram um computador. Agora, vamos calcular as probabilidades dos clientes comprarem um computador. Seja P(w1). Da mesma forma, a probabilidade de os clientes não comprarem um cliente é P(w2).

Agora faremos uma comparação básica para nossos futuros clientes.

Para um novo cliente,

Se P(w1) > P(w2), então o cliente comprará um computador (w1)

E, se P(w2) > P(w1), então o cliente não comprará um computador (w2)

Aqui, resolvemos nosso problema de decisão.

Mas, qual é o problema com este método básico de decisão? Bem, a maioria de vocês pode ter adivinhado certo. Com base apenas em registros anteriores, ele sempre dará a mesma decisão para todos os futuros clientes. Isso é ilógico e absurdo.

Por isso, precisamos de algo que nos ajude a tomar melhores decisões para futuros clientes. Fazemos isso introduzindo alguns recursos. Digamos que adicionamos um recurso 'x' onde 'x' denota a idade do cliente. Agora, com esse recurso adicional, poderemos tomar melhores decisões.

Para fazer isso, precisamos saber o que é o Teorema de Bayes.

Leia: Tipos de Aprendizagem Supervisionada

Teorema de Bayes e Teoria da Decisão

Para nossa classe w1 e recurso 'x', temos:

P(w1 | x) = P(x | w1) * P(w1) P(x)

Existem 4 termos nesta fórmula que precisamos entender:

1. Prior – P(w1) é a Probabilidade Anterior de que w1 seja verdadeiro antes que os dados sejam observados
2. Posterior – P(w1 | x) é a Probabilidade Posterior de que w1 seja verdadeiro após os dados serem observados.
3. Evidência - P(x) é a Probabilidade Total dos Dados
4. Probabilidade – P(x | w1) é a informação sobre w1 fornecida por 'x'

P(w1 | x) é lido como Probabilidade de w1 dado x

Mais precisamente, é a probabilidade de um cliente comprar um computador, dada a idade de um cliente específico.

Agora, estamos prontos para tomar nossa decisão:

Para um novo cliente,

Se P(w1 | x) > P(w2 | x), então o cliente comprará um computador (w1)

E, se P(w2 | x) > P(w1 | x), então o cliente não comprará um computador (w2)

Essa decisão parece mais lógica e confiável, pois temos alguns recursos aqui para trabalhar e nossa decisão é baseada nos recursos de nossos novos clientes e também em registros anteriores e não apenas em registros anteriores, como em casos anteriores.

Agora, pela fórmula, você pode ver que para ambas as nossas classes w1 e w2, nosso denominador P(x) é constante. Assim, podemos utilizar essa ideia e formar outra forma de decisão como abaixo:

Se P(x | w1)*P(w1) > P(x | w2)*P(w2), então o cliente comprará um computador (w1)

E, se P(x | w2)*P(w2) > P(x | w1)*P(w1), então o cliente não comprará um computador (w2)

Podemos notar aqui um fato interessante. Se, de alguma forma, nossas probabilidades anteriores P(w1) e P(w2) forem iguais, ainda podemos tomar nossa decisão com base em nossas probabilidades de verossimilhança P(x | w1) e P(x | w2). Da mesma forma, se nossas probabilidades de probabilidade são iguais, podemos tomar decisões com base em nossas probabilidades anteriores P(w1) e P(w2).

Deve ler: tipos de modelos de regressão em aprendizado de máquina

Cálculo de Risco

Como mencionado anteriormente, sempre haverá algum 'risco' ou erro na decisão. Portanto, também precisamos determinar a probabilidade de erro cometido em uma decisão. Isso é muito simples e vou demonstrar isso em termos de visualizações.

Vamos considerar que temos alguns dados e tomamos uma decisão de acordo com a Teoria da Decisão Bayesiana.

Obtemos um gráfico mais ou menos como abaixo:

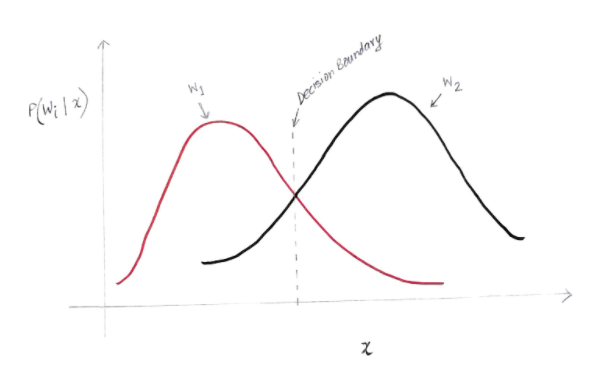
O eixo y é a probabilidade posterior P(w(i) | x) e o eixo x é nossa característica 'x'. O eixo onde a probabilidade posterior para ambas as classes é igual, esse eixo é chamado de nosso limite de decisão.

Então, no limite de decisão:

P(w1 | x) = P(w2 | x)

Assim, à esquerda do limite de decisão, decidimos a favor de w1 (comprar um computador) e à direita do limite de decisão, decidimos a favor de w2 (não comprar um computador).

Mas, como você pode ver no gráfico, há uma magnitude diferente de zero de w2 à esquerda do limite de decisão. Além disso, há alguma magnitude diferente de zero de w1 à direita do limite de decisão. Essa extensão de outra classe sobre outra classe é o que você chama de erro de risco ou probabilidade.

Cálculo do Erro de Probabilidade

Para calcular a probabilidade de erro para a classe w1, precisamos encontrar a probabilidade de que a classe seja w2 na área que está à esquerda do limite de decisão. Da mesma forma, a probabilidade de erro para a classe w2 é a probabilidade de que a classe seja w1 na área que está à direita do limite de decisão.

Matematicamente falando, o erro mínimo para a classe:

w1 é P(w2 | x)

E para a classe w2 é P(w1 | x)

Você obteve o erro de probabilidade desejado. Simples, não é?

Então, qual é o erro total agora?

Vamos denotar a probabilidade de erro total para uma característica x ser P(E | x). O erro total para um recurso x seria a soma de todas as probabilidades de erro para esse recurso x. Usando integração simples, podemos resolver isso e o resultado que obtemos é:

P(E | x) = mínimo (P(w1 | x) , P(w2 | x))

Portanto, nossa probabilidade de erro total é o mínimo da probabilidade posterior para ambas as classes. Estamos fazendo o mínimo de uma aula porque, no final das contas, daremos uma decisão com base na outra aula.

Conclusão

Examinamos detalhadamente as aplicações discretas da Teoria da Decisão Bayesiana. Agora você conhece o Teorema de Bayes e seus termos. Você também sabe como aplicar o Teorema de Bayes para tomar uma decisão. Você também aprendeu a determinar o erro na decisão que tomou.

Se você estiver interessado em aprender mais sobre aprendizado de máquina, confira o PG Diploma in Machine Learning & AI do IIIT-B e upGrad, projetado para profissionais que trabalham e oferece mais de 450 horas de treinamento rigoroso, mais de 30 estudos de caso e atribuições, IIIT- B Status de ex-aluno, mais de 5 projetos práticos práticos e assistência de trabalho com as principais empresas.