Memahami Teori Keputusan Bayesian Dengan Contoh Sederhana

pengantar

Kami menghadapi banyak masalah klasifikasi dalam kehidupan nyata. Misalnya, sebuah toko elektronik mungkin perlu mengetahui apakah pelanggan tertentu berdasarkan usia tertentu, akan membeli komputer atau tidak. Melalui artikel ini, kita akan memperkenalkan sebuah metode bernama 'Bayesian Decision Theory' yang membantu kita dalam mengambil keputusan apakah akan memilih kelas dengan probabilitas 'x' atau kelas berlawanan dengan probabilitas 'y' berdasarkan fitur tertentu.

Definisi

Teori Keputusan Bayesian adalah pendekatan sederhana namun mendasar untuk berbagai masalah seperti klasifikasi pola. Seluruh tujuan Teori Keputusan Bayes adalah untuk membantu kita memilih keputusan yang akan memberikan kita 'risiko' paling sedikit. Selalu ada semacam risiko yang melekat pada setiap keputusan yang kita pilih. Kami akan membahas risiko yang terlibat dalam klasifikasi ini nanti di artikel ini.

Keputusan Dasar

Mari kita ambil contoh di mana perusahaan toko elektronik ingin mengetahui apakah pelanggan akan membeli komputer atau tidak. Jadi kami memiliki dua kelas pembelian berikut:

w1 – Ya (Pelanggan akan membeli komputer)

w2 – Tidak (Pelanggan tidak akan membeli komputer)

Sekarang, kita akan melihat catatan masa lalu dari database pelanggan kita. Kami akan mencatat jumlah pelanggan yang membeli komputer dan juga jumlah pelanggan yang tidak membeli komputer. Sekarang, kita akan menghitung probabilitas pelanggan membeli komputer. Misalkan P(w1). Demikian pula, probabilitas pelanggan tidak membeli pelanggan adalah P(w2).

Sekarang kami akan melakukan perbandingan dasar untuk pelanggan masa depan kami.

Untuk pelanggan baru,

Jika P(w1) > P(w2), maka pelanggan akan membeli komputer (w1)

Dan, jika P(w2) > P(w1), maka pelanggan tidak akan membeli komputer (w2)

Di sini, kami telah memecahkan masalah keputusan kami.

Tapi, apa masalahnya dengan metode Dasar Keputusan ini? Yah, sebagian besar dari Anda mungkin sudah menebak dengan benar. Berdasarkan catatan sebelumnya, itu akan selalu memberikan keputusan yang sama untuk semua pelanggan masa depan. Ini tidak logis dan absurd.

Jadi kami membutuhkan sesuatu yang akan membantu kami dalam membuat keputusan yang lebih baik untuk pelanggan masa depan. Kami melakukannya dengan memperkenalkan beberapa fitur. Katakanlah kita menambahkan fitur 'x' di mana 'x' menunjukkan usia pelanggan. Sekarang dengan fitur tambahan ini, kami akan dapat membuat keputusan yang lebih baik.

Untuk melakukan ini, kita perlu tahu apa itu Teorema Bayes.

Baca: Jenis-Jenis Pembelajaran Terawasi

Teorema Bayes dan Teori Keputusan

Untuk kelas kami w1 dan fitur 'x', kami memiliki:

P(w1 | x) = P(x | w1) * P(w1) P(x)

Ada 4 istilah dalam rumus ini yang perlu kita pahami:

1. Prior – P(w1) adalah Probabilitas Prior bahwa w1 benar sebelum data diamati
2. Posterior – P(w1 | x) adalah Probabilitas Posterior bahwa w1 benar setelah data diamati.
3. Bukti – P(x) adalah Probabilitas Total Data
4. Kemungkinan – P(x | w1) adalah informasi tentang w1 yang disediakan oleh 'x'

P(w1 | x) dibaca sebagai Probabilitas w1 diberikan x

Lebih tepatnya, ini adalah probabilitas bahwa pelanggan akan membeli komputer, mengingat usia pelanggan tertentu.

Sekarang, kami siap untuk membuat keputusan:

Untuk pelanggan baru,

Jika P(w1 | x) > P(w2 | x), maka pelanggan akan membeli komputer (w1)

Dan, jika P(w2 | x) > P(w1 | x), maka pelanggan tidak akan membeli komputer (w2)

Keputusan ini tampaknya lebih logis dan dapat dipercaya karena kami memiliki beberapa fitur di sini untuk dikerjakan dan keputusan kami didasarkan pada fitur pelanggan baru kami dan juga catatan masa lalu dan bukan hanya catatan masa lalu seperti pada kasus sebelumnya.

Sekarang, dari rumus, Anda dapat melihat bahwa untuk kedua kelas kami w1 dan w2, penyebut kami P(x) adalah konstan. Jadi, kita dapat memanfaatkan ide ini dan dapat membentuk bentuk lain dari keputusan seperti di bawah ini:

Jika P(x | w1)*P(w1) > P(x | w2)*P(w2), maka pelanggan akan membeli komputer (w1)

Dan, jika P(x | w2)*P(w2) > P(x | w1)*P(w1), maka pelanggan tidak akan membeli komputer (w2)

Kita bisa melihat fakta menarik di sini. Jika bagaimanapun, probabilitas sebelumnya P(w1) dan P(w2) adalah sama, kita masih dapat membuat keputusan berdasarkan probabilitas kemungkinan kita P(x | w1) dan P(x | w2). Demikian pula, jika probabilitas kemungkinan kita sama, kita dapat membuat keputusan berdasarkan probabilitas sebelumnya P(w1) dan P(w2).

Wajib Dibaca: Jenis-Jenis Model Regresi dalam Machine Learning

Perhitungan Risiko

Seperti disebutkan sebelumnya, akan selalu ada sejumlah 'risiko' atau kesalahan yang dibuat dalam keputusan. Jadi, kita juga perlu menentukan probabilitas kesalahan yang dibuat dalam suatu keputusan. Ini sangat sederhana dan saya akan menunjukkannya dalam hal visualisasi.

Mari kita anggap kita memiliki beberapa data dan kita telah membuat keputusan menurut Teori Keputusan Bayesian.

Kami mendapatkan grafik agak seperti di bawah ini:

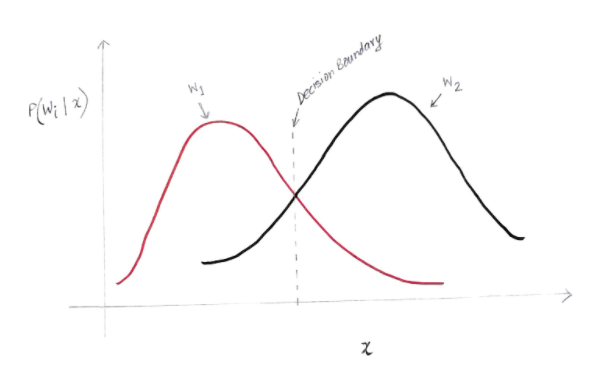
Sumbu y adalah probabilitas posterior P(w(i) | x) dan sumbu x adalah fitur kami 'x'. Sumbu di mana probabilitas posterior untuk kedua kelas sama, sumbu itu disebut batas keputusan kita.

Jadi pada Batas Keputusan:

P(w1 | x) = P(w2 | x)

Jadi di sebelah kiri batas keputusan, kami memutuskan mendukung w1 (membeli komputer) dan di sebelah kanan batas keputusan, kami memutuskan mendukung w2 (tidak membeli komputer).

Tetapi, seperti yang Anda lihat dalam grafik, ada beberapa besaran yang tidak nol dari w2 di sebelah kiri batas keputusan. Juga, ada beberapa besaran non-nol dari w1 di sebelah kanan batas keputusan. Perpanjangan kelas lain di atas kelas lain ini adalah apa yang Anda sebut kesalahan risiko atau probabilitas.

Perhitungan Probabilitas Kesalahan

Untuk menghitung peluang kesalahan untuk kelas w1, kita perlu mencari peluang bahwa kelas tersebut adalah w2 di daerah yang berada di sebelah kiri batas keputusan. Demikian pula, peluang kesalahan untuk kelas w2 adalah peluang bahwa kelas tersebut adalah w1 di daerah yang berada di sebelah kanan batas keputusan.

Secara matematis, kesalahan minimum untuk kelas:

w1 adalah P(w2 | x)

Dan untuk kelas w2 adalah P(w1 | x)

Anda mendapatkan kesalahan probabilitas yang Anda inginkan. Sederhana, bukan?

Jadi apa total kesalahan sekarang?

Mari kita nyatakan probabilitas kesalahan total untuk fitur x menjadi P(E | x). Kesalahan total untuk fitur x akan menjadi jumlah dari semua probabilitas kesalahan untuk fitur x itu. Dengan menggunakan integrasi sederhana, kita dapat menyelesaikan ini dan hasil yang kita dapatkan adalah:

P(E | x) = minimum (P(w1 | x) , P(w2 | x))

Oleh karena itu, probabilitas kesalahan total kami adalah probabilitas posterior minimum untuk kedua kelas. Kami mengambil minimal satu kelas karena pada akhirnya kami akan memberikan keputusan berdasarkan kelas lain.

Kesimpulan

Kami telah melihat secara rinci aplikasi diskrit Teori Keputusan Bayesian. Anda sekarang tahu Teorema Bayes dan istilah-istilahnya. Anda juga tahu bagaimana menerapkan Teorema Bayes dalam mengambil keputusan. Anda juga telah belajar bagaimana menentukan kesalahan dalam keputusan yang telah Anda buat.

Jika Anda tertarik untuk mempelajari lebih lanjut tentang pembelajaran mesin, lihat PG Diploma IIIT-B & upGrad dalam Pembelajaran Mesin & AI yang dirancang untuk para profesional yang bekerja dan menawarkan 450+ jam pelatihan ketat, 30+ studi kasus & tugas, IIIT- B Status alumni, 5+ proyek batu penjuru praktis & bantuan pekerjaan dengan perusahaan-perusahaan top.