Comprendre la théorie de la décision bayésienne avec un exemple simple

introduction

Nous rencontrons beaucoup de problèmes de classification dans la vie réelle. Par exemple, un magasin d'électronique peut avoir besoin de savoir si un client particulier, en fonction d'un certain âge, va acheter un ordinateur ou non. À travers cet article, nous allons introduire une méthode nommée "Théorie de la décision bayésienne" qui nous aide à prendre des décisions quant à la sélection d'une classe avec une probabilité "x" ou d'une classe opposée avec une probabilité "y" basée sur une certaine caractéristique.

Définition

La théorie de la décision bayésienne est une approche simple mais fondamentale à une variété de problèmes comme la classification des modèles. L'objectif de la théorie de la décision de Bayes est de nous aider à sélectionner les décisions qui nous coûteront le moins de "risque". Il y a toujours une sorte de risque attaché à toute décision que nous choisissons. Nous passerons en revue les risques liés à cette classification plus loin dans cet article.

Décision de base

Prenons un exemple où une entreprise de magasin d'électronique veut savoir si un client va acheter un ordinateur ou non. Nous avons donc les deux classes d'achat suivantes :

w1 – Oui (le client achètera un ordinateur)

w2 – Non (le client n'achètera pas d'ordinateur)

Maintenant, nous allons examiner les enregistrements passés de notre base de données clients. Nous noterons le nombre de clients qui achètent des ordinateurs et aussi le nombre de clients qui n'achètent pas d'ordinateur. Maintenant, nous allons calculer les probabilités que les clients achètent un ordinateur. Soit P(w1). De même, la probabilité que les clients n'achètent pas un client est P(w2).

Nous allons maintenant faire une comparaison de base pour nos futurs clients.

Pour un nouveau client,

Si P(w1) > P(w2), alors le client achètera un ordinateur (w1)

Et, si P(w2) > P(w1), alors le client n'achètera pas d'ordinateur (w2)

Ici, nous avons résolu notre problème de décision.

Mais quel est le problème avec cette méthode de décision de base ? Eh bien, la plupart d'entre vous ont peut-être deviné juste. Basé uniquement sur les enregistrements précédents, il donnera toujours la même décision pour tous les futurs clients. C'est illogique et absurde.

Nous avons donc besoin de quelque chose qui nous aidera à prendre de meilleures décisions pour les futurs clients. Nous le faisons en introduisant certaines fonctionnalités. Disons que nous ajoutons une fonctionnalité « x », où « x » indique l'âge du client. Maintenant, avec cette fonctionnalité supplémentaire, nous serons en mesure de prendre de meilleures décisions.

Pour ce faire, nous devons savoir ce qu'est le théorème de Bayes.

Lire : Types d'apprentissage supervisé

Théorème de Bayes et théorie de la décision

Pour notre classe w1 et fonctionnalité 'x', nous avons :

P(w1 | x) = P(x | w1) * P(w1) P(x)

Il y a 4 termes dans cette formule que nous devons comprendre :

1. Prior – P(w1) est la probabilité a priori que w1 est vraie avant que les données ne soient observées
2. Postérieur – P(w1 | x) est la probabilité postérieure que w1 soit vrai après l'observation des données.
3. Preuve – P(x) est la probabilité totale des données
4. Probabilité – P(x | w1) est l'information sur w1 fournie par 'x'

P(w1 | x) se lit comme la probabilité de w1 étant donné x

Plus précisément, c'est la probabilité qu'un client achète un ordinateur, compte tenu de l'âge d'un client spécifique.

Maintenant, nous sommes prêts à prendre notre décision :

Pour un nouveau client,

Si P(w1 | x) > P(w2 | x), alors le client achètera un ordinateur (w1)

Et, si P(w2 | x) > P(w1 | x), alors le client n'achètera pas d'ordinateur (w2)

Cette décision semble plus logique et digne de confiance puisque nous avons ici quelques fonctionnalités sur lesquelles travailler et notre décision est basée sur les caractéristiques de nos nouveaux clients ainsi que sur les enregistrements passés et pas seulement sur les enregistrements passés comme dans les cas précédents.

Maintenant, à partir de la formule, vous pouvez voir que pour nos deux classes w1 et w2, notre dénominateur P(x) est constant. Ainsi, nous pouvons utiliser cette idée et former une autre forme de décision comme ci-dessous :

Si P(x | w1)*P(w1) > P(x | w2)*P(w2), alors le client achètera un ordinateur (w1)

Et, si P(x | w2)*P(w2) > P(x | w1)*P(w1), alors le client n'achètera pas d'ordinateur (w2)

Nous pouvons remarquer ici un fait intéressant. Si d'une manière ou d'une autre, nos probabilités antérieures P(w1) et P(w2) sont égales, nous pouvons toujours être en mesure de prendre notre décision en fonction de nos probabilités de vraisemblance P(x | w1) et P(x | w2). De même, si nos probabilités de vraisemblance sont égales, nous pouvons prendre des décisions basées sur nos probabilités antérieures P(w1) et P(w2).

Doit lire : Types de modèles de régression dans l'apprentissage automatique

Calcul du risque

Comme mentionné précédemment, il y aura toujours un certain "risque" ou une erreur dans la décision. Donc, nous devons également déterminer la probabilité d'erreur commise dans une décision. C'est très simple et je vais le démontrer en termes de visualisations.

Considérons que nous avons des données et que nous avons pris une décision selon la théorie de la décision bayésienne.

On obtient un graphique un peu comme ci-dessous :

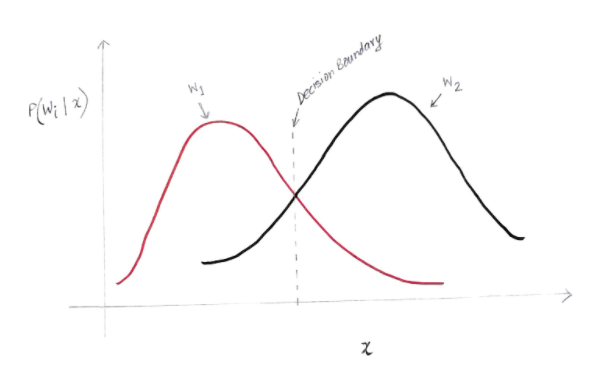
L'axe des y est la probabilité a posteriori P(w(i) | x) et l'axe des x est notre caractéristique 'x'. L'axe où la probabilité a posteriori pour les deux classes est égale, cet axe est appelé notre limite de décision.

Ainsi, à la limite de décision :

P(w1 | x) = P(w2 | x)

Ainsi, à gauche de la frontière de décision, nous décidons en faveur de w1 (acheter un ordinateur) et à droite de la frontière de décision, nous décidons en faveur de w2 (ne pas acheter d'ordinateur).

Mais, comme vous pouvez le voir sur le graphique, il y a une magnitude non nulle de w2 à gauche de la frontière de décision. En outre, il existe une amplitude non nulle de w1 à droite de la limite de décision. Cette extension d'une autre classe sur une autre classe est ce que vous appelez une erreur de risque ou de probabilité.

Calcul de l'erreur de probabilité

Pour calculer la probabilité d'erreur pour la classe w1, nous devons trouver la probabilité que la classe soit w2 dans la zone située à gauche de la limite de décision. De même, la probabilité d'erreur pour la classe w2 est la probabilité que la classe soit w1 dans la zone située à droite de la frontière de décision.

Mathématiquement parlant, l'erreur minimale pour la classe :

w1 est P(w2 | x)

Et pour la classe w2 est P(w1 | x)

Vous avez obtenu votre erreur de probabilité souhaitée. Simple, n'est-ce pas ?

Alors, quelle est l'erreur totale maintenant ?

Dénotons la probabilité d'erreur totale pour une caractéristique x d'être P(E | x). L'erreur totale pour une caractéristique x serait la somme de toutes les probabilités d'erreur pour cette caractéristique x. En utilisant une intégration simple, nous pouvons résoudre ce problème et le résultat que nous obtenons est :

P(E | x) = minimum (P(w1 | x) , P(w2 | x))

Par conséquent, notre probabilité d'erreur totale est le minimum de la probabilité a posteriori pour les deux classes. Nous prenons le minimum d'une classe car finalement nous donnerons une décision basée sur l'autre classe.

Conclusion

Nous avons examiné en détail les applications discrètes de la théorie bayésienne de la décision. Vous connaissez maintenant le théorème de Bayes et ses termes. Vous savez également comment appliquer le théorème de Bayes pour prendre une décision. Vous avez également appris à déterminer l'erreur dans la décision que vous avez prise.

Si vous souhaitez en savoir plus sur l'apprentissage automatique, consultez le diplôme PG en apprentissage automatique et IA de IIIT-B & upGrad, conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, IIIT- Statut B Alumni, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.