فهم نظرية القرار بايز بمثال بسيط

مقدمة

نواجه الكثير من مشاكل التصنيف في الحياة الواقعية. على سبيل المثال ، قد يحتاج متجر إلكتروني إلى معرفة ما إذا كان عميل معين بناءً على عمر معين سيشتري جهاز كمبيوتر أم لا. من خلال هذه المقالة ، سنقدم طريقة تسمى "نظرية القرار البايزية" والتي تساعدنا في اتخاذ القرارات بشأن اختيار فئة ذات احتمالية "x" أو فئة معاكسة باحتمالية "y" بناءً على ميزة معينة.

تعريف

نظرية القرار البايزي هي طريقة بسيطة ولكنها أساسية لمجموعة متنوعة من المشاكل مثل تصنيف الأنماط. الغرض الكامل من نظرية قرار بايز هو مساعدتنا في اختيار القرارات التي ستكلفنا أقل "مخاطرة". هناك دائمًا نوع من المخاطر المرتبطة بأي قرار نختاره. سنستعرض المخاطر التي ينطوي عليها هذا التصنيف لاحقًا في هذه المقالة.

القرار الأساسي

لنأخذ مثالاً حيث تريد شركة متجر إلكترونيات معرفة ما إذا كان العميل سيشتري جهاز كمبيوتر أم لا. لذلك لدينا فئتا الشراء التاليتان:

w1 - نعم (سيشتري العميل جهاز كمبيوتر)

W2 - لا (لن يشتري العميل جهاز كمبيوتر)

الآن ، سننظر في السجلات السابقة لقاعدة بيانات عملائنا. سنقوم بتدوين عدد العملاء الذين يشترون أجهزة الكمبيوتر وكذلك عدد العملاء الذين لا يشترون جهاز كمبيوتر. الآن ، سنقوم بحساب احتمالات شراء العملاء لجهاز كمبيوتر. فليكن P (w1). وبالمثل ، فإن احتمال عدم شراء العملاء للعميل هو P (W2).

الآن سنقوم بإجراء مقارنة أساسية لعملائنا في المستقبل.

للعميل الجديد ،

إذا كان P (w1)> P (w2) ، فسيشتري العميل جهاز كمبيوتر (w1)

وإذا كانت P (w2)> P (w1) ، فلن يشتري العميل جهاز كمبيوتر (W2)

هنا ، قمنا بحل مشكلة قرارنا.

لكن ما هي مشكلة طريقة القرار الأساسية هذه؟ حسنًا ، ربما خمّن معظمكم بشكل صحيح. استنادًا إلى السجلات السابقة فقط ، ستعطي دائمًا نفس القرار لجميع العملاء في المستقبل. هذا غير منطقي وعبثي.

لذلك نحن بحاجة إلى شيء من شأنه أن يساعدنا في اتخاذ قرارات أفضل للعملاء في المستقبل. نقوم بذلك من خلال تقديم بعض الميزات. لنفترض أننا أضفنا ميزة "x" حيث تشير "x" إلى عمر العميل. الآن مع هذه الميزة المضافة ، سنتمكن من اتخاذ قرارات أفضل.

للقيام بذلك ، نحتاج إلى معرفة ما هي نظرية بايز.

اقرأ: أنواع التعلم الخاضع للإشراف

نظرية بايز ونظرية القرار

بالنسبة لفصلنا w1 والميزة 'x' ، لدينا:

الفوسفور (w1 | x) = P (x | w1) * P (w1) P (x)

هناك 4 مصطلحات في هذه الصيغة نحتاج إلى فهمها:

1. Pre - P (w1) هو الاحتمال المسبق بأن يكون w1 صحيحًا قبل ملاحظة البيانات
2. الخلفي - P (w1 | x) هو الاحتمال الخلفي الذي يكون w1 صحيحًا بعد ملاحظة البيانات.
3. الدليل - P (x) هو إجمالي الاحتمالية للبيانات
4. الاحتمالية - P (x | w1) هي المعلومات حول w1 التي يقدمها "x"

تتم قراءة P (w1 | x) على أنها احتمال w1 معطى x

بتعبير أدق ، هو احتمال أن يشتري العميل جهاز كمبيوتر ، بالنظر إلى عمر العميل المحدد.

الآن ، نحن على استعداد لاتخاذ قرارنا:

للعميل الجديد ،

إذا كان P (w1 | x)> P (w2 | x) ، فسيشتري العميل جهاز كمبيوتر (w1)

وإذا كانت P (w2 | x)> P (w1 | x) ، فلن يشتري العميل جهاز كمبيوتر (W2)

يبدو هذا القرار أكثر منطقية وجديرة بالثقة نظرًا لأن لدينا بعض الميزات هنا للعمل عليها ويستند قرارنا إلى ميزات عملائنا الجدد وكذلك السجلات السابقة وليس فقط السجلات السابقة كما في الحالات السابقة.

الآن ، من الصيغة ، يمكنك أن ترى أنه لكل من الفئتين w1 و w2 ، فإن المقام P (x) ثابت. لذلك ، يمكننا الاستفادة من هذه الفكرة ويمكننا تشكيل شكل آخر من أشكال القرار على النحو التالي:

إذا كان P (x | w1) * P (w1)> P (x | w2) * P (w2) ، فسيشتري العميل جهاز كمبيوتر (w1)

وإذا كان P (x | w2) * P (w2)> P (x | w1) * P (w1) ، فلن يشتري العميل جهاز كمبيوتر (w2)

يمكننا أن نلاحظ حقيقة مثيرة للاهتمام هنا. إذا كانت احتماليتنا السابقة P (w1) و P (w2) بطريقة ما متساوية ، فلا يزال بإمكاننا اتخاذ قرارنا بناءً على احتمالية الاحتمالية P (x | w1) و P (x | w2). وبالمثل ، إذا كانت احتمالات الاحتمالية لدينا متساوية ، فيمكننا اتخاذ قرارات بناءً على احتمالاتنا السابقة P (W1) و P (W2).

يجب أن تقرأ: أنواع نماذج الانحدار في التعلم الآلي

حساب المخاطر

كما ذكرنا سابقًا ، سيكون هناك دائمًا قدر من "المخاطرة" أو الخطأ في القرار. لذلك ، نحتاج أيضًا إلى تحديد احتمال الخطأ الذي تم اتخاذه في القرار. هذا بسيط للغاية وسأوضح ذلك من حيث التصورات.

دعونا نفكر في أن لدينا بعض البيانات وقد اتخذنا قرارًا وفقًا لنظرية القرار Bayesian.

نحصل على رسم بياني إلى حد ما مثل أدناه:

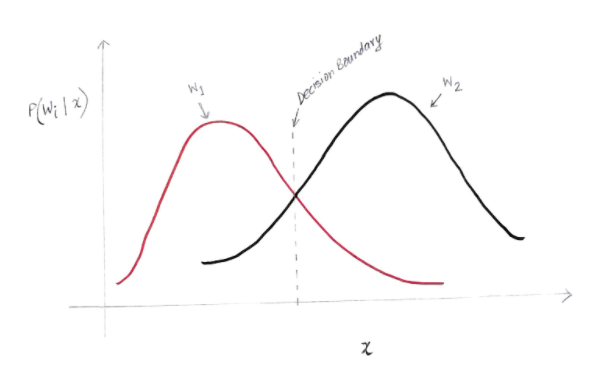
المحور y هو الاحتمال الخلفي P (w (i) | x) والمحور x هو ميزتنا "x". المحور الذي يتساوى فيه الاحتمال اللاحق لكلتا الفئتين ، يسمى هذا المحور حدود قرارنا.

إذن عند حدود القرار:

الفوسفور (w1 | x) = P (w2 | x)

لذلك على يسار حدود القرار ، نقرر لصالح w1 (شراء جهاز كمبيوتر) وعلى يمين حدود القرار ، نقرر لصالح w2 (عدم شراء جهاز كمبيوتر).

ولكن ، كما ترى في الرسم البياني ، يوجد مقدار غير صفري لـ w2 على يسار حدود القرار. أيضًا ، يوجد مقدار غير صفري لـ w1 على يمين حدود القرار. هذا الامتداد لفئة أخرى على فئة أخرى هو ما تسميه خطأ خطر أو احتمال.

احتساب خطأ احتمالي

لحساب احتمال الخطأ للفئة w1 ، نحتاج إلى إيجاد احتمال أن تكون الفئة w2 في المنطقة الواقعة على يسار حد القرار. وبالمثل ، فإن احتمال الخطأ للفئة w2 هو احتمال أن تكون الفئة w1 في المنطقة الواقعة على يمين حدود القرار.

من الناحية الرياضية ، الحد الأدنى للخطأ للفئة:

w1 هو P (w2 | x)

وبالنسبة للفئة w2 هو P (w1 | x)

لقد حصلت على خطأ الاحتمال المطلوب. بسيط ، أليس كذلك؟

إذن ما هو الخطأ الإجمالي الآن؟

دعونا نشير إلى احتمال الخطأ الكلي للميزة x لتكون P (E | x). إجمالي الخطأ لميزة x سيكون مجموع كل احتمالات الخطأ لتلك الميزة x. باستخدام التكامل البسيط ، يمكننا حل هذا والنتيجة التي نحصل عليها هي:

P (E | x) = الحد الأدنى (P (w1 | x) ، P (w2 | x))

لذلك ، فإن احتمال الخطأ الكلي لدينا هو الحد الأدنى من الاحتمال اللاحق لكلا الفئتين. نحن نأخذ الحد الأدنى من الفصل لأننا في النهاية سنعطي قرارًا بناءً على الفصل الآخر.

خاتمة

لقد نظرنا بالتفصيل في التطبيقات المنفصلة لنظرية القرار البايزية. أنت الآن تعرف نظرية بايز وشروطها. أنت تعرف أيضًا كيفية تطبيق نظرية بايز في اتخاذ القرار. لقد تعلمت أيضًا كيفية تحديد الخطأ في القرار الذي اتخذته.

إذا كنت مهتمًا بمعرفة المزيد حول التعلم الآلي ، فراجع دبلوم PG في IIIT-B & upGrad في التعلم الآلي والذكاء الاصطناعي المصمم للمهنيين العاملين ويقدم أكثر من 450 ساعة من التدريب الصارم ، وأكثر من 30 دراسة حالة ومهمة ، IIIT- حالة الخريجين B ، أكثر من 5 مشاريع تتويجا عملية ومساعدة وظيفية مع أفضل الشركات.