Comprendere la teoria della decisione bayesiana con un semplice esempio

introduzione

Nella vita reale incontriamo molti problemi di classificazione. Ad esempio, un negozio di elettronica potrebbe aver bisogno di sapere se un determinato cliente in base a una certa età acquisterà un computer o meno. Attraverso questo articolo, introdurremo un metodo chiamato "Teoria della decisione bayesiana" che ci aiuta a decidere se selezionare una classe con probabilità "x" o una classe opposta con probabilità "y" in base a una determinata caratteristica.

Definizione

La teoria della decisione bayesiana è un approccio semplice ma fondamentale a una varietà di problemi come la classificazione dei modelli. L'intero scopo della teoria delle decisioni di Bayes è di aiutarci a selezionare le decisioni che ci costeranno il minor "rischio". C'è sempre una sorta di rischio connesso a qualsiasi decisione che scegliamo. Analizzeremo il rischio connesso a questa classificazione più avanti in questo articolo.

Decisione di base

Facciamo un esempio in cui un'azienda di negozi di elettronica vuole sapere se un cliente acquisterà un computer o meno. Quindi abbiamo le seguenti due classi di acquisto:

w1 – Sì (il cliente acquisterà un computer)

w2 – No (il cliente non acquisterà un computer)

Ora esamineremo i record passati del nostro database dei clienti. Prenderemo nota del numero di clienti che acquistano computer e anche del numero di clienti che non acquistano un computer. Ora calcoleremo le probabilità che i clienti acquistino un computer. Sia P(w1). Allo stesso modo, la probabilità che i clienti non acquistino un cliente è P(w2).

Ora faremo un confronto di base per i nostri futuri clienti.

Per un nuovo cliente,

Se P(w1) > P(w2), il cliente acquisterà un computer (w1)

E, se P(w2) > P(w1), il cliente non acquisterà un computer (w2)

Qui abbiamo risolto il nostro problema decisionale.

Ma qual è il problema con questo metodo Decisionale di base? Bene, la maggior parte di voi potrebbe aver indovinato. Basandosi solo sui record precedenti, darà sempre la stessa decisione a tutti i futuri clienti. Questo è illogico e assurdo.

Quindi abbiamo bisogno di qualcosa che ci aiuti a prendere decisioni migliori per i futuri clienti. Lo facciamo introducendo alcune funzionalità. Supponiamo di aggiungere una funzione 'x' dove 'x' indica l'età del cliente. Ora con questa funzione aggiunta, saremo in grado di prendere decisioni migliori.

Per fare questo, dobbiamo sapere cos'è il teorema di Bayes.

Leggi: Tipi di apprendimento supervisionato

Teorema di Bayes e teoria delle decisioni

Per la nostra classe w1 e caratteristica 'x', abbiamo:

P(w1 | x) = P(x | w1) * P(w1) P(x)

Ci sono 4 termini in questa formula che dobbiamo capire:

1. Prior – P(w1) è la probabilità a priori che w1 sia vero prima che i dati vengano osservati
2. Posteriore – P(w1 | x) è la Probabilità Posteriore che w1 è vero dopo che i dati sono stati osservati.
3. Evidenza – P(x) è la Probabilità Totale dei Dati
4. Probabilità – P(x | w1) è l'informazione su w1 fornita da 'x'

P(w1 | x) si legge come Probabilità di w1 data x

Più precisamente, è la probabilità che un cliente acquisti un computer, data l'età di un determinato cliente.

Ora siamo pronti per prendere la nostra decisione:

Per un nuovo cliente,

Se P(w1 | x) > P(w2 | x), il cliente acquisterà un computer (w1)

E, se P(w2 | x) > P(w1 | x), il cliente non acquisterà un computer (w2)

Questa decisione sembra più logica e affidabile poiché abbiamo alcune funzionalità su cui lavorare e la nostra decisione si basa sulle caratteristiche dei nostri nuovi clienti e anche sui record passati e non solo sui record passati come nei casi precedenti.

Ora, dalla formula, puoi vedere che per entrambe le nostre classi w1 e w2, il nostro denominatore P(x) è costante. Quindi, possiamo utilizzare questa idea e possiamo formare un'altra forma di decisione come di seguito:

Se P(x | w1)*P(w1) > P(x | w2)*P(w2), il cliente acquisterà un computer (w1)

E, se P(x | w2)*P(w2) > P(x | w1)*P(w1), il cliente non acquisterà un computer (w2)

Possiamo notare un fatto interessante qui. Se in qualche modo le nostre probabilità a priori P(w1) e P(w2) sono uguali, possiamo ancora essere in grado di prendere la nostra decisione in base alle nostre probabilità di verosimiglianza P(x | w1) e P(x | w2). Allo stesso modo, se le nostre probabilità di verosimiglianza sono uguali, possiamo prendere decisioni in base alle nostre probabilità a priori P(w1) e P(w2).

Da leggere: Tipi di modelli di regressione nell'apprendimento automatico

Calcolo del rischio

Come accennato in precedenza, ci sarà sempre una certa quantità di "rischio" o errore commesso nella decisione. Quindi, dobbiamo anche determinare la probabilità di errore in una decisione. Questo è molto semplice e lo dimostrerò in termini di visualizzazioni.

Consideriamo di avere alcuni dati e di aver preso una decisione secondo la teoria della decisione bayesiana.

Otteniamo un grafico in qualche modo simile al seguente:

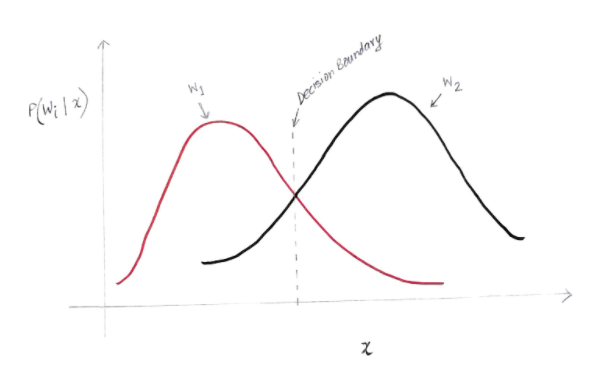
L'asse y è la probabilità a posteriori P(w(i) | x) e l'asse x è la nostra caratteristica 'x'. L'asse in cui la probabilità a posteriori per entrambe le classi è uguale, quell'asse è chiamato il nostro limite di decisione.

Quindi a Decision Boundary:

P(w1 | x) = P(w2 | x)

Quindi, a sinistra del limite di decisione, decidiamo a favore di w1 (acquisto di un computer) ea destra del limite di decisione, decidiamo a favore di w2 (non acquisto di un computer).

Ma, come puoi vedere nel grafico, c'è una magnitudine diversa da zero di w2 a sinistra del confine della decisione. Inoltre, c'è una magnitudine diversa da zero di w1 a destra del confine di decisione. Questa estensione di un'altra classe rispetto a un'altra classe è ciò che chiami un errore di rischio o di probabilità.

Calcolo dell'errore di probabilità

Per calcolare la probabilità di errore per la classe w1, dobbiamo trovare la probabilità che la classe sia w2 nell'area che è a sinistra del confine di decisione. Allo stesso modo, la probabilità di errore per la classe w2 è la probabilità che la classe sia w1 nell'area che è a destra del confine di decisione.

Matematicamente parlando, l'errore minimo per la classe:

w1 è P(w2 | x)

E per la classe w2 è P(w1 | x)

Hai ottenuto l'errore di probabilità desiderato. Semplice, non è vero?

Quindi qual è l'errore totale ora?

Indichiamo la probabilità che l'errore totale di una caratteristica x sia P(E | x). L'errore totale per una caratteristica x sarebbe la somma di tutte le probabilità di errore per quella caratteristica x. Usando una semplice integrazione, possiamo risolverlo e il risultato che otteniamo è:

P(E | x) = minimo (P(w1 | x) , P(w2 | x))

Pertanto, la nostra probabilità di errore totale è il minimo della probabilità a posteriori per entrambe le classi. Stiamo prendendo il minimo di una classe perché alla fine daremo una decisione basata sull'altra classe.

Conclusione

Abbiamo esaminato in dettaglio le applicazioni discrete della teoria della decisione bayesiana. Ora conosci il teorema di Bayes e i suoi termini. Sai anche come applicare il teorema di Bayes nel prendere una decisione. Hai anche imparato a determinare l'errore nella decisione che hai preso.

Se sei interessato a saperne di più sull'apprendimento automatico, dai un'occhiata al Diploma PG di IIIT-B e upGrad in Machine Learning e AI, progettato per i professionisti che lavorano e offre oltre 450 ore di formazione rigorosa, oltre 30 casi di studio e incarichi, IIIT- B Status di Alumni, oltre 5 progetti pratici pratici e assistenza sul lavoro con le migliori aziende.