簡単な例でベイズ決定理論を理解する

序章

私たちは実生活で多くの分類問題に遭遇します。 たとえば、電気店は、特定の年齢に基づく特定の顧客がコンピュータを購入するかどうかを知る必要がある場合があります。 この記事では、特定の機能に基づいて、確率が「x」のクラスを選択するか、確率が「y」の反対のクラスを選択するかを決定するのに役立つ「ベイズ決定理論」という名前のメソッドを紹介します。

意味

ベイジアン決定理論は、パターン分類などのさまざまな問題に対する単純ですが基本的なアプローチです。 ベイズ決定理論の全体的な目的は、「リスク」が最も少ない決定を選択できるようにすることです。 私たちが選択する決定には、常に何らかのリスクが伴います。 この記事の後半で、この分類に伴うリスクについて説明します。

基本的な決定

ある電気店の会社が、顧客がコンピューターを購入するかどうかを知りたがっている例を見てみましょう。 したがって、次の2つの購入クラスがあります。

w1 –はい（お客様はコンピューターを購入します）

w2 –いいえ（お客様はコンピューターを購入しません）

次に、顧客データベースの過去の記録を調べます。 コンピュータを購入している顧客の数と、コンピュータを購入していない顧客の数を書き留めます。 次に、顧客がコンピューターを購入する確率を計算します。 P（w1）とします。 同様に、顧客が顧客を購入しない確率はP（w2）です。

次に、将来の顧客のために基本的な比較を行います。

新規のお客様は、

P（w1）> P（w2）の場合、顧客はコンピューター（w1）を購入します。

また、P（w2）> P（w1）の場合、顧客はコンピューターを購入しません（w2）

ここで、決定問題を解決しました。

しかし、この基本的な決定方法の問題は何ですか？ さて、あなたのほとんどは正しく推測したかもしれません。 以前の記録に基づいて、将来のすべての顧客に対して常に同じ決定を下します。 これは非論理的でばかげています。

したがって、将来の顧客のためにより良い意思決定を行うのに役立つ何かが必要です。 いくつかの機能を導入することでそれを実現します。 機能「x」を追加するとします。ここで、「x」は顧客の年齢を示します。 この追加機能により、より適切な決定を下すことができるようになります。

これを行うには、ベイズの定理が何であるかを知る必要があります。

読む：教師あり学習の種類

ベイズの定理と決定理論

クラスw1と機能'x'の場合、次のようになります。

P（w1 | x） = P（x | w1）* P（w1） P（x）

この式には、理解する必要のある4つの用語があります。

1. 事前確率– P（w1）は、データが観測される前にw1が真である事前確率です。
2. 事後– P（w1 | x）は、データが観測された後にw1が真である事後確率です。
3. 証拠– P（x）はデータの全確率です
4. 尤度– P（x | w1）は、「x」によって提供されるw1に関する情報です。

P（w1 | x）は、xが与えられた場合のw1の確率として読み取られます。

より正確には、特定の顧客の年齢を考えると、顧客がコンピューターを購入する確率です。

これで、決定を下す準​​備が整いました。

新規のお客様は、

P（w1 | x）> P（w2 | x）の場合、顧客はコンピューター（w1）を購入します。

また、P（w2 | x）> P（w1 | x）の場合、顧客はコンピューター（w2）を購入しません。

この決定は、ここで取り組むべきいくつかの機能があり、以前の場合のように過去の記録だけでなく、新しい顧客の特徴と過去の記録にも基づいているため、より論理的で信頼できるように思われます。

ここで、式から、クラスw1とw2の両方で、分母P（x）が定数であることがわかります。 したがって、このアイデアを利用して、次のような別の形式の決定を行うことができます。

P（x | w1）* P（w1）> P（x | w2）* P（w2）の場合、顧客はコンピューター（w1）を購入します。

また、P（x | w2）* P（w2）> P（x | w1）* P（w1）の場合、顧客はコンピューターを購入しません（w2）

ここで興味深い事実に気付くことができます。 どういうわけか、事前確率P（w1）とP（w2）が等しい場合でも、尤度確率P（x | w1）とP（x | w2）に基づいて決定を下すことができます。 同様に、尤度確率が等しい場合、事前確率P（w1）とP（w2）に基づいて決定を下すことができます。

必読：機械学習における回帰モデルの種類

リスク計算

先に述べたように、決定には常にある程度の「リスク」またはエラーがあります。 したがって、決定で行われたエラーの確率も決定する必要があります。 これは非常に単純であり、視覚化の観点からそれを示します。

いくつかのデータがあり、ベイズ決定理論に従って決定を下したと考えてみましょう。

以下のようなグラフが得られます。

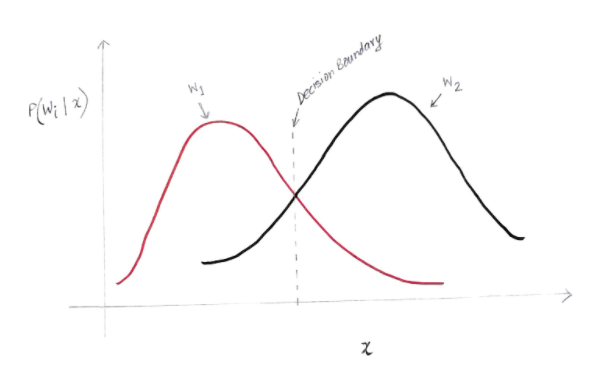
y軸は事後確率P（w（i）| x）であり、x軸は特徴'x'です。 両方のクラスの事後確率が等しい軸。その軸は、決定境界と呼ばれます。

したがって、決定境界で：

P（w1 | x）= P（w2 | x）

したがって、決定境界の左側では、w1（コンピューターを購入する）を支持することを決定し、決定境界の右側では、w2（コンピューターを購入しない）を支持することを決定します。

ただし、グラフからわかるように、決定境界の左側にはゼロ以外の大きさのw2があります。 また、決定境界の右側には、ゼロ以外の大きさのw1があります。 別のクラスに対する別のクラスのこの拡張は、リスクまたは確率エラーと呼ばれるものです。

確率誤差の計算

クラスw1のエラーの確率を計算するには、決定境界の左側にある領域でクラスがw2である確率を見つける必要があります。 同様に、クラスw2のエラーの確率は、決定境界の右側にある領域でクラスがw1である確率です。

数学的に言えば、クラスの最小エラー：

w1はP（w2 | x）です

また、クラスw2の場合はP（w1 | x）です。

希望する確率エラーが発生しました。 簡単ですね。

では、現在の合計エラーは何ですか？

特徴xの全誤差の確率をP（E | x）としましょう。 特徴xの合計誤差は、その特徴xのすべての誤差確率の合計になります。 単純な統合を使用して、これを解決でき、得られる結果は次のとおりです。

P（E | x）=最小（P（w1 | x）、P（w2 | x））

したがって、合計エラーの確率は、両方のクラスの事後確率の最小値です。 最終的には他のクラスに基づいて決定を下すため、クラスは最小限に抑えています。

結論

ベイズ決定理論の個別のアプリケーションについて詳しく見てきました。 これで、ベイズの定理とその用語がわかりました。 また、決定を下す際にベイズの定理を適用する方法も知っています。 あなたはまた、あなたが下した決定の誤りを決定する方法を学びました。

機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのPGディプロマをご覧ください。これは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディと課題、IIIT-を提供します。 B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との仕事の支援。