ทำความเข้าใจทฤษฎีการตัดสินใจแบบเบย์ด้วยตัวอย่างง่ายๆ

บทนำ

เราพบปัญหาการจำแนกประเภทมากมายในชีวิตจริง ตัวอย่างเช่น ร้านค้าอิเล็กทรอนิกส์อาจจำเป็นต้องรู้ว่าลูกค้าเฉพาะช่วงอายุหนึ่งจะซื้อคอมพิวเตอร์หรือไม่ ในบทความนี้ เราจะแนะนำวิธีการที่ชื่อ 'ทฤษฎีการตัดสินใจแบบเบย์' ซึ่งช่วยให้เราตัดสินใจว่าจะเลือกคลาสที่มีความน่าจะเป็น 'x' หรือคลาสตรงข้ามที่มีความน่าจะเป็น 'y' ตามคุณลักษณะบางอย่าง

คำนิยาม

ทฤษฎีการตัดสินใจแบบเบย์ เป็นแนวทางที่เรียบง่ายแต่เป็นพื้นฐานสำหรับปัญหาที่หลากหลาย เช่น การจำแนกรูปแบบ จุดประสงค์ทั้งหมดของทฤษฎีการตัดสินใจแบบเบย์คือการช่วยเราเลือกการตัดสินใจที่จะทำให้เรามี 'ความเสี่ยง' น้อยที่สุด การตัดสินใจใด ๆ ที่เราเลือกมีความเสี่ยงอยู่เสมอ เราจะผ่านความเสี่ยงที่เกี่ยวข้องกับการจัดหมวดหมู่นี้ในบทความนี้

การตัดสินใจขั้นพื้นฐาน

ให้เรายกตัวอย่างที่บริษัทร้านขายอุปกรณ์อิเล็กทรอนิกส์ต้องการทราบว่าลูกค้าจะซื้อคอมพิวเตอร์หรือไม่ ดังนั้นเราจึงมีคลาสการซื้อสองคลาสต่อไปนี้:

w1 – ใช่ (ลูกค้าจะซื้อคอมพิวเตอร์)

w2 – ไม่ (ลูกค้าจะไม่ซื้อคอมพิวเตอร์)

ตอนนี้ เราจะดูบันทึกในอดีตของฐานข้อมูลลูกค้าของเรา เราจะจดจำนวนลูกค้าที่ซื้อคอมพิวเตอร์และจำนวนลูกค้าที่ไม่ซื้อคอมพิวเตอร์ด้วย ตอนนี้เราจะคำนวณความน่าจะเป็นของลูกค้าที่ซื้อคอมพิวเตอร์ ปล่อยให้มันเป็น P(w1) ในทำนองเดียวกัน ความน่าจะเป็นที่ลูกค้าไม่ซื้อลูกค้าคือ P(w2)

ตอนนี้เราจะทำการเปรียบเทียบพื้นฐานสำหรับลูกค้าในอนาคตของเรา

สำหรับลูกค้าใหม่

ถ้า P(w1) > P(w2) ลูกค้าจะซื้อคอมพิวเตอร์ (w1)

และถ้า P(w2) > P(w1) ลูกค้าจะไม่ซื้อคอมพิวเตอร์ (w2)

ที่นี่เราได้แก้ปัญหาการตัดสินใจของเราแล้ว

แต่ปัญหาของวิธีการตัดสินใจขั้นพื้นฐานนี้คืออะไร? พวกคุณส่วนใหญ่อาจเดาถูกแล้ว อ้างอิงจากบันทึกก่อนหน้านี้ จะเป็นการตัดสินใจแบบเดียวกันสำหรับลูกค้าในอนาคตทั้งหมด นี่เป็นเรื่องไร้เหตุผลและไร้สาระ

ดังนั้นเราจึงต้องการบางสิ่งที่จะช่วยเราในการตัดสินใจที่ดีขึ้นสำหรับลูกค้าในอนาคต เราทำได้โดยการแนะนำคุณสมบัติบางอย่าง สมมติว่าเราเพิ่มคุณลักษณะ 'x' โดยที่ 'x' หมายถึงอายุของลูกค้า ด้วยฟีเจอร์ที่เพิ่มเข้ามานี้ เราจะสามารถตัดสินใจได้ดีขึ้น

ในการทำสิ่งนี้ เราต้องรู้ว่าทฤษฎีบทเบย์คืออะไร

อ่าน: ประเภทของการเรียนรู้ภายใต้การดูแล

ทฤษฎีบทเบย์และทฤษฎีการตัดสินใจ

สำหรับคลาส w1 และฟีเจอร์ 'x' เรามี:

P(w1 | x) = P(x | w1) * P(w1) P(x)

มีคำศัพท์ 4 คำในสูตรนี้ที่เราต้องเข้าใจ:

1. ก่อนหน้า – P(w1) คือความน่าจะเป็นก่อนหน้าที่ w1 เป็นจริงก่อนที่จะสังเกตข้อมูล
2. หลัง – P(w1 | x) คือความน่าจะเป็นหลังที่ w1 เป็นจริงหลังจากสังเกตข้อมูล
3. หลักฐาน – P(x) คือความน่าจะเป็นทั้งหมดของข้อมูล
4. ความน่าจะเป็น – P(x | w1) เป็นข้อมูลเกี่ยวกับ w1 ที่จัดเตรียมโดย 'x'

P(w1 | x) ถูกอ่านว่าเป็นความน่าจะเป็นของ w1 ที่กำหนด x

แม่นยำยิ่งขึ้นคือความน่าจะเป็นที่ลูกค้าจะซื้อคอมพิวเตอร์โดยพิจารณาจากอายุของลูกค้าที่เฉพาะเจาะจง

ตอนนี้เราพร้อมที่จะตัดสินใจแล้ว:

สำหรับลูกค้าใหม่

ถ้า P(w1 | x) > P(w2 | x) ลูกค้าจะซื้อคอมพิวเตอร์ (w1)

และถ้า P(w2 | x) > P(w1 | x) ลูกค้าจะไม่ซื้อคอมพิวเตอร์ (w2)

การตัดสินใจนี้ดูสมเหตุสมผลและน่าเชื่อถือมากกว่า เนื่องจากเรามีคุณสมบัติบางอย่างที่ต้องดำเนินการ และการตัดสินใจของเราขึ้นอยู่กับคุณลักษณะของลูกค้าใหม่และบันทึกในอดีต ไม่ใช่แค่บันทึกในอดีตเหมือนในกรณีก่อนหน้านี้

จากสูตร คุณจะเห็นว่าสำหรับทั้งคลาส w1 และ w2 ตัวส่วน P(x) ของเรามีค่าคงที่ ดังนั้นเราจึงสามารถนำแนวคิดนี้ไปใช้และสร้างการตัดสินใจในรูปแบบอื่นได้ดังนี้:

ถ้า P(x | w1)*P(w1) > P(x | w2)*P(w2) ลูกค้าจะซื้อคอมพิวเตอร์ (w1)

และหาก P(x | w2)*P(w2) > P(x | w1)*P(w1) ลูกค้าจะไม่ซื้อคอมพิวเตอร์ (w2)

เราสามารถสังเกตข้อเท็จจริงที่น่าสนใจได้ที่นี่ ถ้าอย่างไรก็ตาม ความน่าจะเป็นก่อนหน้าของเรา P(w1) และ P(w2) เท่ากัน เราก็ยังสามารถตัดสินใจได้โดยพิจารณาจากความน่าจะเป็นของเรา P(x | w1) และ P(x | w2) ในทำนองเดียวกัน หากความน่าจะเป็นของเราเท่ากัน เราสามารถตัดสินใจโดยพิจารณาจากความน่าจะเป็นก่อนหน้าของเรา P(w1) และ P(w2)

ต้องอ่าน: ประเภทของแบบจำลองการถดถอยในการเรียนรู้ของเครื่อง

การคำนวณความเสี่ยง

ดังที่ได้กล่าวไว้ก่อนหน้านี้ มักจะมี 'ความเสี่ยง' หรือข้อผิดพลาดในการตัดสินใจอยู่เสมอ ดังนั้น เราต้องกำหนดความน่าจะเป็นของข้อผิดพลาดในการตัดสินใจด้วย สิ่งนี้ง่ายมาก และฉันจะแสดงให้เห็นในแง่ของการสร้างภาพข้อมูล

ให้เราพิจารณาว่าเรามีข้อมูลบางส่วนและเราได้ทำการตัดสินใจตามทฤษฎีการตัดสินใจแบบเบย์

เราจะได้กราฟดังนี้

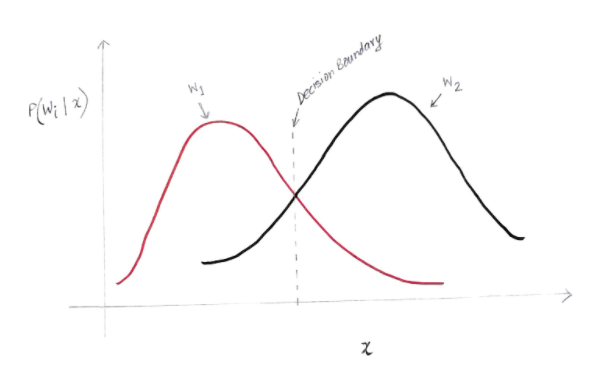
แกน y คือความน่าจะเป็นภายหลัง P(w(i) | x) และแกน x คือคุณลักษณะ 'x' ของเรา แกนที่ความน่าจะเป็นภายหลังสำหรับทั้งสองคลาสเท่ากัน แกนนั้นเรียกว่าขอบเขตการตัดสินใจของเรา

ดังนั้นที่ขอบเขตการตัดสินใจ:

P(w1 | x) = P(w2 | x)

ดังนั้น ทางด้านซ้ายของขอบเขตการตัดสินใจ เราตัดสินใจเลือก w1(ซื้อคอมพิวเตอร์) และทางด้านขวาของขอบเขตการตัดสินใจ เราตัดสินใจเลือก w2(ไม่ซื้อคอมพิวเตอร์)

แต่อย่างที่คุณเห็นในกราฟ มีบางขนาดที่ไม่เป็นศูนย์ของ w2 ทางด้านซ้ายของขอบเขตการตัดสินใจ นอกจากนี้ยังมีบางขนาดที่ไม่เป็นศูนย์ของ w1 ทางด้านขวาของขอบเขตการตัดสินใจ ส่วนขยายของคลาสอื่นเหนือคลาสอื่นคือสิ่งที่คุณเรียกว่าความเสี่ยงหรือข้อผิดพลาดความน่าจะเป็น

การคำนวณข้อผิดพลาดความน่าจะเป็น

ในการคำนวณความน่าจะเป็นของข้อผิดพลาดสำหรับคลาส w1 เราจำเป็นต้องค้นหาความน่าจะเป็นที่คลาสนั้นเป็น w2 ในพื้นที่ทางด้านซ้ายของขอบเขตการตัดสินใจ ในทำนองเดียวกัน ความน่าจะเป็นของข้อผิดพลาดสำหรับคลาส w2 คือความน่าจะเป็นที่คลาสนั้นเป็น w1 ในพื้นที่ทางด้านขวาของขอบเขตการตัดสินใจ

ในทางคณิตศาสตร์ ข้อผิดพลาดขั้นต่ำสำหรับชั้นเรียน:

w1 คือ P(w2 | x)

และสำหรับคลาส w2 คือ P(w1 | x)

คุณได้รับข้อผิดพลาดความน่าจะเป็นที่ต้องการ ง่ายใช่มั้ย?

ดังนั้นข้อผิดพลาดทั้งหมดในขณะนี้คืออะไร?

ให้เราแสดงถึงความน่าจะเป็นของข้อผิดพลาดทั้งหมดสำหรับจุดสนใจ x ที่จะเป็น P(E | x) ข้อผิดพลาดทั้งหมดสำหรับจุดสนใจ x จะเป็นผลรวมของความน่าจะเป็นทั้งหมดของข้อผิดพลาดสำหรับจุดสนใจ x โดยใช้การรวมอย่างง่าย เราสามารถแก้ปัญหานี้ได้ และผลลัพธ์ที่เราได้รับคือ:

P(E | x) = ต่ำสุด (P(w1 | x) , P(w2 | x))

ดังนั้น ความน่าจะเป็นของข้อผิดพลาดทั้งหมดจึงเป็นค่าต่ำสุดของความน่าจะเป็นภายหลังสำหรับทั้งสองคลาส เรากำลังเรียนขั้นต่ำของชั้นเรียนเพราะในที่สุดเราจะให้การตัดสินใจตามชั้นเรียนอื่น

บทสรุป

เราได้ศึกษารายละเอียดการใช้งานทฤษฎีการตัดสินใจแบบเบย์อย่างละเอียดแล้ว ตอนนี้คุณรู้ทฤษฎีบทเบย์และข้อกำหนดแล้ว คุณยังรู้วิธีการใช้ทฤษฎีบทเบย์ในการตัดสินใจ คุณยังได้เรียนรู้วิธีระบุข้อผิดพลาดในการตัดสินใจของคุณอีกด้วย

หากคุณสนใจที่จะเรียนรู้เพิ่มเติมเกี่ยวกับแมชชีนเลิร์นนิง โปรดดูที่ IIIT-B & upGrad's PG Diploma in Machine Learning & AI ซึ่งออกแบบมาสำหรับมืออาชีพที่ทำงานและมีการฝึกอบรมที่เข้มงวดมากกว่า 450 ชั่วโมง กรณีศึกษาและการมอบหมายมากกว่า 30 รายการ IIIT- สถานะศิษย์เก่า B, 5+ โครงการหลักที่ใช้งานได้จริง & ความช่วยเหลือด้านงานกับบริษัทชั้นนำ