Comprender la teoría de la decisión bayesiana con un ejemplo simple

Introducción

Nos encontramos con muchos problemas de clasificación en la vida real. Por ejemplo, una tienda de electrónica podría necesitar saber si un cliente en particular de cierta edad va a comprar una computadora o no. A través de este artículo, vamos a presentar un método llamado 'Teoría de decisión bayesiana' que nos ayuda a tomar decisiones sobre si seleccionar una clase con probabilidad 'x' o una clase opuesta con probabilidad 'y' en función de una determinada característica.

Definición

La teoría de la decisión bayesiana es un enfoque simple pero fundamental para una variedad de problemas como la clasificación de patrones. Todo el propósito de la teoría de la decisión de Bayes es ayudarnos a seleccionar decisiones que nos cuesten el menor "riesgo". Siempre hay algún tipo de riesgo asociado a cualquier decisión que elijamos. Veremos el riesgo involucrado en esta clasificación más adelante en este artículo.

Decisión básica

Tomemos un ejemplo en el que una empresa de tiendas de electrónica quiere saber si un cliente va a comprar una computadora o no. Entonces tenemos las siguientes dos clases de compra:

w1 – Sí (El cliente comprará una computadora)

w2 – No (El cliente no comprará una computadora)

Ahora, examinaremos los registros anteriores de nuestra base de datos de clientes. Anotaremos la cantidad de clientes que compran computadoras y también la cantidad de clientes que no compran una computadora. Ahora, calcularemos las probabilidades de que los clientes compren una computadora. Sea P(w1). De manera similar, la probabilidad de que los clientes no compren un cliente es P(w2).

Ahora haremos una comparación básica para nuestros futuros clientes.

Para un nuevo cliente,

Si P(w1) > P(w2), entonces el cliente comprará una computadora (w1)

Y, si P(w2) > P(w1), entonces el cliente no comprará una computadora (w2)

Aquí, hemos resuelto nuestro problema de decisión.

Pero, ¿cuál es el problema de este método básico de Decisión? Bueno, la mayoría de ustedes podría haber acertado. Basado solo en registros anteriores, siempre dará la misma decisión para todos los futuros clientes. Esto es ilógico y absurdo.

Así que necesitamos algo que nos ayude a tomar mejores decisiones para futuros clientes. Lo hacemos introduciendo algunas características. Digamos que agregamos una característica 'x' donde 'x' denota la edad del cliente. Ahora con esta función añadida, podremos tomar mejores decisiones.

Para hacer esto, necesitamos saber qué es el Teorema de Bayes.

Leer: Tipos de aprendizaje supervisado

Teorema de Bayes y Teoría de la Decisión

Para nuestra clase w1 y característica 'x', tenemos:

P(w1 | x) = P(x | w1) * P(w1) P(x)

Hay 4 términos en esta fórmula que debemos entender:

1. Previa: P(w1) es la probabilidad previa de que w1 sea verdadera antes de que se observen los datos
2. Posterior: P(w1 | x) es la probabilidad posterior de que w1 sea cierto después de observar los datos.
3. Evidencia: P(x) es la probabilidad total de los datos
4. Probabilidad – P(x | w1) es la información sobre w1 proporcionada por 'x'

P(w1 | x) se lee como Probabilidad de w1 dado x

Más precisamente, es la probabilidad de que un cliente compre una computadora, dada la edad de un cliente específico.

Ahora, estamos listos para tomar nuestra decisión:

Para un nuevo cliente,

Si P(w1 | x) > P(w2 | x), entonces el cliente comprará una computadora (w1)

Y, si P(w2 | x) > P(w1 | x), entonces el cliente no comprará una computadora (w2)

Esta decisión parece más lógica y confiable ya que aquí tenemos algunas características en las que trabajar y nuestra decisión se basa en las características de nuestros nuevos clientes y también en los registros anteriores y no solo en los registros anteriores como en casos anteriores.

Ahora, a partir de la fórmula, puedes ver que para ambas clases w1 y w2, nuestro denominador P(x) es constante. Entonces, podemos utilizar esta idea y podemos formar otra forma de decisión como se muestra a continuación:

Si P(x | w1)*P(w1) > P(x | w2)*P(w2), entonces el cliente comprará una computadora (w1)

Y, si P(x | w2)*P(w2) > P(x | w1)*P(w1), entonces el cliente no comprará una computadora (w2)

Podemos notar un hecho interesante aquí. Si de alguna manera, nuestras probabilidades previas P(w1) y P(w2) son iguales, aún podemos tomar nuestra decisión en función de nuestras probabilidades de verosimilitud P(x | w1) y P(x | w2). De manera similar, si nuestras probabilidades de verosimilitud son iguales, podemos tomar decisiones basadas en nuestras probabilidades previas P(w1) y P(w2).

Debe leer: Tipos de modelos de regresión en el aprendizaje automático

Cálculo de riesgo

Como se mencionó anteriormente, siempre habrá una cierta cantidad de 'riesgo' o error en la decisión. Entonces, también necesitamos determinar la probabilidad de error cometido en una decisión. Esto es muy simple y lo demostraré en términos de visualizaciones.

Consideremos que tenemos algunos datos y hemos tomado una decisión de acuerdo con la Teoría de Decisión Bayesiana.

Obtenemos un gráfico similar al siguiente:

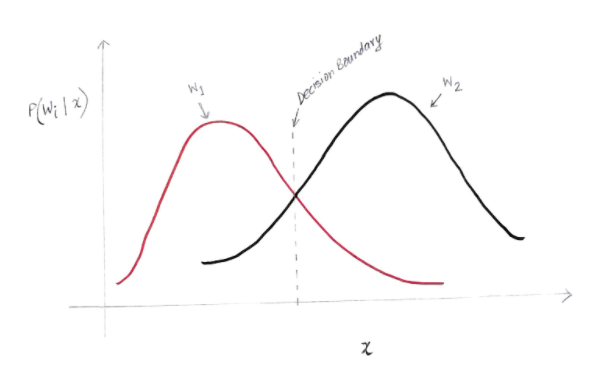
El eje y es la probabilidad posterior P(w(i) | x) y el eje x es nuestra característica 'x'. El eje donde la probabilidad posterior para ambas clases es igual, ese eje se llama nuestro límite de decisión.

Entonces, en el límite de decisión:

P(w1 | x) = P(w2 | x)

Entonces, a la izquierda del límite de decisión, decidimos a favor de w1 (comprar una computadora) ya la derecha del límite de decisión, decidimos a favor de w2 (no comprar una computadora).

Pero, como puede ver en el gráfico, hay una magnitud distinta de cero de w2 a la izquierda del límite de decisión. Además, hay una magnitud distinta de cero de w1 a la derecha del límite de decisión. Esta extensión de otra clase sobre otra clase es lo que llamas un error de riesgo o probabilidad.

Cálculo de error de probabilidad

Para calcular la probabilidad de error de la clase w1, necesitamos encontrar la probabilidad de que la clase sea w2 en el área que está a la izquierda del límite de decisión. De manera similar, la probabilidad de error para la clase w2 es la probabilidad de que la clase sea w1 en el área que está a la derecha del límite de decisión.

Matemáticamente hablando, el error mínimo para la clase:

w1 es P(w2 | x)

Y para la clase w2 es P(w1 | x)

Obtuviste el error de probabilidad deseado. Sencillo, ¿no?

Entonces, ¿cuál es el error total ahora?

Denotemos la probabilidad de error total de una característica x como P(E | x). El error total de una característica x sería la suma de todas las probabilidades de error de esa característica x. Usando integración simple, podemos resolver esto y el resultado que obtenemos es:

P(E | x) = mínimo (P(w1 | x) , P(w2 | x))

Por lo tanto, nuestra probabilidad de error total es el mínimo de la probabilidad posterior para ambas clases. Estamos tomando el mínimo de una clase porque finalmente daremos una decisión basada en la otra clase.

Conclusión

Hemos visto en detalle las aplicaciones discretas de la teoría de la decisión bayesiana. Ahora conoce el Teorema de Bayes y sus términos. También sabe cómo aplicar el Teorema de Bayes para tomar una decisión. También ha aprendido a determinar el error en la decisión que ha tomado.

Si está interesado en obtener más información sobre el aprendizaje automático, consulte el Diploma PG en aprendizaje automático e IA de IIIT-B y upGrad, que está diseñado para profesionales que trabajan y ofrece más de 450 horas de capacitación rigurosa, más de 30 estudios de casos y asignaciones, IIIT- B Estado de exalumno, más de 5 proyectos prácticos finales prácticos y asistencia laboral con las mejores empresas.