Zrozumienie Bayesowskiej teorii decyzji na prostym przykładzie

Wstęp

W prawdziwym życiu napotykamy wiele problemów z klasyfikacją. Na przykład sklep elektroniczny może potrzebować wiedzieć, czy konkretny klient w określonym wieku zamierza kupić komputer, czy nie. W tym artykule przedstawimy metodę o nazwie „Teoria decyzji Bayesa”, która pomaga nam w podejmowaniu decyzji, czy wybrać klasę z prawdopodobieństwem „x”, czy klasę przeciwną z prawdopodobieństwem „y” w oparciu o określoną cechę.

Definicja

Bayesowska teoria decyzji jest prostym, ale podstawowym podejściem do różnych problemów, takich jak klasyfikacja wzorców. Całkowitym celem teorii decyzji Bayesa jest pomoc w wyborze decyzji, które będą nas kosztować najmniej „ryzyka”. Z każdą wybraną przez nas decyzją zawsze wiąże się jakieś ryzyko. W dalszej części artykułu omówimy ryzyko związane z tą klasyfikacją.

Podstawowa decyzja

Weźmy przykład, w którym firma zajmująca się sklepem elektronicznym chce wiedzieć, czy klient kupi komputer, czy nie. Mamy więc dwie klasy zakupowe:

w1 – Tak (Klient kupi komputer)

w2 – Nie (Klient nie kupi komputera)

Teraz przyjrzymy się przeszłym zapisom naszej bazy danych klientów. Zanotujemy liczbę klientów kupujących komputery, a także liczbę klientów, którzy nie kupują komputera. Teraz obliczymy prawdopodobieństwa zakupu komputera przez klientów. Niech to będzie P(w1). Podobnie prawdopodobieństwo, że klienci nie kupią klienta, wynosi P(w2).

Teraz zrobimy podstawowe porównanie dla naszych przyszłych klientów.

Dla nowego klienta,

Jeżeli P(w1) > P(w2), to klient kupi komputer (w1)

A jeśli P(w2) > P(w1), to klient nie kupi komputera (w2)

Tutaj rozwiązaliśmy nasz problem decyzyjny.

Ale jaki jest problem z tą podstawową metodą podejmowania decyzji? Cóż, większość z was mogła się domyślić. Bazując na poprzednich rekordach, zawsze poda taką samą decyzję wszystkim przyszłym klientom. To nielogiczne i absurdalne.

Potrzebujemy więc czegoś, co pomoże nam w podejmowaniu lepszych decyzji dla przyszłych klientów. Robimy to, wprowadzając kilka funkcji. Załóżmy, że dodajemy funkcję „x”, gdzie „x” oznacza wiek klienta. Teraz dzięki tej dodanej funkcji będziemy mogli podejmować lepsze decyzje.

Aby to zrobić, musimy wiedzieć, czym jest twierdzenie Bayesa.

Przeczytaj: Rodzaje nadzorowanego uczenia się

Twierdzenie Bayesa i teoria decyzji

Dla naszej klasy w1 i cechy „x” mamy:

P(w1 | x) = P(x | w1) * P(w1) P(x)

W tej formule są 4 terminy, które musimy zrozumieć:

1. Wcześniejsze – P(w1) to prawdopodobieństwo wcześniejsze, że w1 jest prawdziwe przed zaobserwowaniem danych
2. A posteriori – P(w1 | x) to prawdopodobieństwo a posteriori, że w1 jest prawdziwe po zaobserwowaniu danych.
3. Dowód – P(x) to całkowite prawdopodobieństwo danych
4. Prawdopodobieństwo – P(x | w1) to informacja o w1 dostarczona przez 'x'

P(w1 | x) jest odczytywane jako Prawdopodobieństwo w1 przy danym x

A dokładniej, jest to prawdopodobieństwo, że klient kupi komputer, biorąc pod uwagę jego wiek.

Teraz jesteśmy gotowi do podjęcia decyzji:

Dla nowego klienta,

Jeżeli P(w1 | x) > P(w2 | x), to klient kupi komputer (w1)

A jeśli P(w2 | x) > P(w1 | x), to klient nie kupi komputera (w2)

Ta decyzja wydaje się bardziej logiczna i godna zaufania, ponieważ mamy tutaj pewne funkcje, nad którymi możemy pracować, a nasza decyzja opiera się na cechach naszych nowych klientów, a także przeszłych rekordach, a nie tylko przeszłych rekordach, jak we wcześniejszych przypadkach.

Teraz ze wzoru widać, że dla obu naszych klas w1 i w2 nasz mianownik P(x) jest stały. Możemy więc wykorzystać ten pomysł i stworzyć inną formę decyzji, jak poniżej:

Jeżeli P(x | w1)*P(w1) > P(x | w2)*P(w2), to klient kupi komputer (w1)

A jeśli P(x | w2)*P(w2) > P(x | w1)*P(w1), to klient nie kupi komputera (w2)

Dostrzegamy tutaj ciekawostkę. Jeśli w jakiś sposób nasze wcześniejsze prawdopodobieństwa P(w1) i P(w2) są równe, nadal możemy podjąć decyzję na podstawie naszych prawdopodobieństw prawdopodobieństw P(x | w1) i P(x | w2). Podobnie, jeśli nasze prawdopodobieństwa prawdopodobieństwa są równe, możemy podejmować decyzje na podstawie naszych wcześniejszych prawdopodobieństw P(w1) i P(w2).

Musisz przeczytać: rodzaje modeli regresji w uczeniu maszynowym

Obliczanie ryzyka

Jak wspomniano wcześniej, przy podejmowaniu decyzji zawsze pojawia się „ryzyko” lub błąd. Musimy więc również określić prawdopodobieństwo popełnienia błędu w decyzji. To bardzo proste i pokażę to w zakresie wizualizacji.

Załóżmy, że mamy pewne dane i podjęliśmy decyzję zgodnie z Bayesowska teorią decyzji.

Otrzymujemy wykres podobny do poniższego:

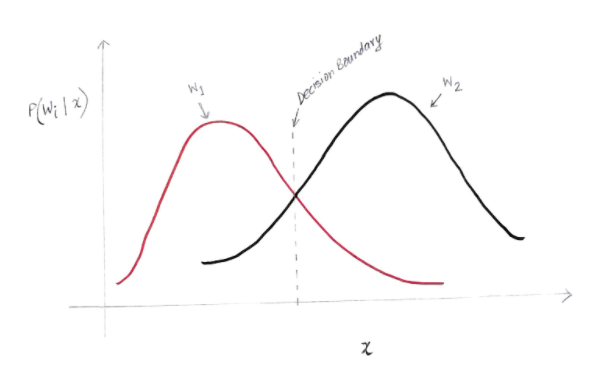
Oś y to prawdopodobieństwo a posteriori P(w(i) | x), a oś x to nasza cecha 'x'. Oś, w której prawdopodobieństwo a posteriori dla obu klas jest równe, nazywa się naszą granicą decyzyjną.

Tak więc na granicy decyzji:

P(w1 | x) = P(w2 | x)

Na lewo od granicy decyzyjnej decydujemy się na w1 (zakup komputera), a na prawo od granicy decyzyjnej na w2 (nie kupowanie komputera).

Ale, jak widać na wykresie, na lewo od granicy decyzyjnej znajduje się pewna niezerowa wielkość w2. Ponadto na prawo od granicy decyzyjnej znajduje się pewna niezerowa wielkość w1. To rozszerzenie innej klasy na inną klasę nazywamy błędem ryzyka lub prawdopodobieństwa.

Obliczanie błędu prawdopodobieństwa

Aby obliczyć prawdopodobieństwo błędu dla klasy w1, musimy znaleźć prawdopodobieństwo, że klasa to w2 w obszarze znajdującym się na lewo od granicy decyzyjnej. Podobnie prawdopodobieństwo błędu dla klasy w2 jest prawdopodobieństwem, że klasa jest w1 w obszarze na prawo od granicy decyzyjnej.

Matematycznie rzecz biorąc, minimalny błąd dla klasy:

w1 to P(w2 | x)

A dla klasy w2 to P(w1 | x)

Otrzymałeś pożądany błąd prawdopodobieństwa. Proste, prawda?

Więc jaki jest teraz całkowity błąd?

Oznaczmy prawdopodobieństwo całkowitego błędu dla cechy x jako P(E | x). Całkowity błąd dla cechy x byłby sumą wszystkich prawdopodobieństw błędu dla tej cechy x. Używając prostej integracji, możemy to rozwiązać, a otrzymany wynik to:

P(E | x) = minimum (P(w1 | x) , P(w2 | x))

Dlatego nasze prawdopodobieństwo całkowitego błędu jest minimum prawdopodobieństwa a posteriori dla obu klas. Bierzemy minimum klasy, ponieważ ostatecznie wydamy decyzję na podstawie drugiej klasy.

Wniosek

Przyjrzeliśmy się szczegółowo dyskretnym zastosowaniom Bayesowskiej Teorii Decyzji. Znasz teraz twierdzenie Bayesa i jego warunki. Wiesz również, jak zastosować twierdzenie Bayesa przy podejmowaniu decyzji. Nauczyłeś się również, jak określić błąd w podjętej decyzji.

Jeśli chcesz dowiedzieć się więcej o uczeniu maszynowym, sprawdź dyplom PG IIIT-B i upGrad w uczeniu maszynowym i sztucznej inteligencji, który jest przeznaczony dla pracujących profesjonalistów i oferuje ponad 450 godzin rygorystycznego szkolenia, ponad 30 studiów przypadków i zadań, IIIT- Status absolwenta B, ponad 5 praktycznych, praktycznych projektów zwieńczenia i pomoc w pracy z najlepszymi firmami.