Karar Ağacı Regresyon İşlevselliği, Terimler, Uygulama [Örnekle]

Başlangıç ​​olarak, bir regresyon modeli, yine sayısal olan bazı girdi değerleri verildiğinde çıktı olarak sayısal bir değer veren bir modeldir. Bu, bir sınıflandırma modelinin yaptığından farklıdır. Test verilerini, belirli bir problem ifadesinde yer alan çeşitli sınıflara veya gruplara sınıflandırır.

Grubun büyüklüğü 2 kadar küçük ve 1000 veya daha fazla büyük olabilir. Doğrusal regresyon, çok değişkenli regresyon, Ridge regresyon, lojistik regresyon ve çok daha fazlası gibi çoklu regresyon modelleri vardır. Karar ağacı regresyon modelleri de bu regresyon modelleri havuzuna aittir.

Tahmine dayalı model, çıktıyı veya hedef değeri belirlemek için ikili kurallardan yararlanan sayısal bir değeri sınıflandırır veya tahmin eder. Karar ağacı modeli adından da anlaşılacağı gibi yaprakları, dalları ve düğümleri olan ağaç benzeri bir modeldir.

Dünyanın En İyi Üniversitelerinden Makine Öğrenimi Çevrimiçi Kursunu Öğrenin . Kariyerinizi hızlandırmak için Master, Executive PGP veya Advanced Certificate Programları kazanın.

Okuyun: Makine Öğrenimi Proje Fikirleri

Hatırlanması Gereken Terminolojiler

Algoritmayı incelemeden önce, hepinizin bilmesi gereken bazı önemli terminolojileri burada bulabilirsiniz.

1. Kök düğüm: Bölmenin başladığı en üstteki düğümdür.
2. Bölme: Tek bir düğümü birden çok alt düğüme bölme işlemi.
3. Terminal düğümü veya yaprak düğümü: Daha fazla bölünmeyen düğümlere terminal düğümleri denir.
4. Budama: Alt düğümlerin kaldırılması işlemi.
5. Ana düğüm: Alt düğümlere ayrılan düğüm.
6. Alt düğüm: Ana düğümden çıkan alt düğümler.

O nasıl çalışır?

Karar ağacı, veri kümesini daha küçük alt kümelere ayırır. Bir karar yaprağı, incelenen özelliğin değerini temsil eden iki veya daha fazla dala ayrılır. Karar ağacındaki en üstteki düğüm, kök düğüm adı verilen en iyi tahmin edicidir. ID3, karar ağacını oluşturan algoritmadır.

Yukarıdan aşağıya bir yaklaşım kullanır ve standart sapmaya göre bölmeler yapılır. Sadece hızlı bir revizyon için, Standart sapma, bir dizi veri noktasının ortalama değerinden dağılım veya dağılım derecesidir. Veri dağılımının genel değişkenliğini ölçer.

Daha yüksek bir dağılım veya değişkenlik değeri, daha büyük, veri noktalarının ortalama değerden daha büyük yayılmasını gösteren standart sapmadır. Numunenin tekdüzeliğini ölçmek için standart sapma kullanıyoruz. Örnek tamamen homojen ise, standart sapması sıfırdır.

Ve benzer şekilde, heterojenlik derecesi ne kadar yüksekse, standart sapma da o kadar büyük olacaktır. Standart sapmayı hesaplamak için numunenin ortalaması ve numune sayısı gereklidir. Matematiksel bir fonksiyon kullanıyoruz - Bölmenin ne zaman durması gerektiğine karar veren Sapma Katsayısı Standart sapmanın tüm örneklerin ortalamasına bölünmesiyle hesaplanır.

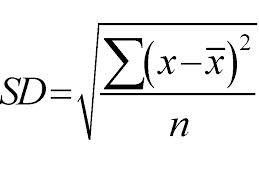
Kaynak

Nihai değer, yaprak düğümlerinin ortalaması olacaktır. Örneğin, Kasım ayının, Kasım ayında (2020'ye kadar) yıllar içinde çeşitli maaşlara ayrılan düğüm olup olmadığını varsayalım. 2021 yılı için, Kasım ayı maaşı, Kasım düğümü altındaki tüm maaşların ortalaması olacaktır.

İki sınıfın veya özelliğin standart sapmasına geçilir (yukarıdaki örnekte olduğu gibi maaş, saatlik veya aylık bazda olabilir). Formül aşağıdaki gibi görünecektir:

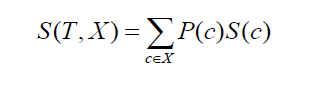
Kaynak

burada P(c), c niteliğinin ortaya çıkma olasılığıdır, S(c), c niteliğinin karşılık gelen standart sapmasıdır. Standart sapmadaki azalma yöntemi, bir veri kümesi bölündükten sonra standart sapmadaki azalmaya dayanır.

Doğru bir karar ağacı oluşturmak için amaç, hesaplama üzerine geri dönen öznitelikleri bulmak ve en yüksek standart sapma azaltmasını döndürmek olmalıdır. Basit bir deyişle, en homojen dallar.

Regresyon için bir Karar ağacı oluşturma süreci dört önemli adımı kapsar.

1. İlk olarak hedef değişkenin standart sapmasını hesaplıyoruz. Hedef değişkeni önceki örneklerde olduğu gibi maaş olarak düşünün. Yerinde örnekle, maaş değerleri setinin standart sapmasını hesaplayacağız.

2. 2. adımda, veri seti farklı özniteliklere bölünür. Nitelikler hakkında konuşurken, hedef değer maaş olduğundan, olası nitelikleri şu şekilde düşünebiliriz - aylar, saatler, patronun ruh hali, atama, şirketteki yıl, vb. Daha sonra, yukarıdaki formül kullanılarak her dal için standart sapma hesaplanır. bu şekilde elde edilen standart sapma, bölünmeden önceki standart sapmadan çıkarılır. Elde edilen sonuca standart sapma azalması denir.

3. Fark önceki adımda belirtildiği gibi hesaplandıktan sonra, en iyi öznitelik, standart sapma azaltma değerinin en büyük olduğu özniteliktir. Bu, bölünmeden önceki standart sapmanın, bölünmeden önceki standart sapmadan daha büyük olması gerektiği anlamına gelir. Aslında, farkın modu alınır ve bunun tersi de mümkündür.

4. Tüm veri seti, seçilen özniteliğin önemine göre sınıflandırılır. Yapraksız dallarda, mevcut tüm veriler işlenene kadar bu yöntem özyinelemeli olarak devam ettirilir. Şimdi, standart sapma azaltma değerine dayalı olarak ayın en iyi bölme özelliği olarak seçildiğini düşünün. Yani her ay için 12 şubemiz olacak. Bu dallar, kalan nitelikler kümesinden en iyi niteliği seçmek için daha da bölünecektir.

5. Gerçekte, bazı bitirme kriterlerine ihtiyacımız var. Bunun için %10 gibi belirli bir eşik değerin altına düşen bir dal için sapma katsayısı veya CV'den yararlanıyoruz . Bu kriteri sağladığımızda ağaç oluşturma sürecini durdururuz. Daha fazla bölme olmadığı için, bu özniteliğin altına düşen değer, o düğüm altındaki tüm değerlerin ortalaması olacaktır.

uygulama

Karar Ağacı Regresyonu, Python dili ve scikit-learn kitaplığı kullanılarak uygulanabilir. sklearn.tree.DecisionTreeRegressor altında bulunabilir.

Önemli parametrelerden bazıları şunlardır:

1. kriter: Bir bölünmenin kalitesini ölçmek için. Değeri “mse” veya ortalama karesel hata, “friedman_mse” ve “mae” veya ortalama mutlak hata olabilir. Varsayılan değer mse'dir.
2. max_depth: Ağacın maksimum derinliğini temsil eder. Varsayılan değer Yok'tur.
3. max_features: En iyi bölünmeye karar verirken aranacak özelliklerin sayısını temsil eder. Varsayılan değer Yok'tur.
4. ayırıcı: Bu parametre, her düğümde bölmeyi seçmek için kullanılır. Mevcut değerler “en iyi” ve “rastgele”dir. Varsayılan değer en iyisidir.

Kontrol edin: Makine Öğrenimi Mülakat Soruları

sklearn belgelerinden örnek

>>> sklearn.datasets'ten load_diabetes'i içe aktarın

>>> sklearn.model_selection'dan cross_val_score'u içe aktarın

>>> sklearn.tree'den DecisionTreeRegressor'u içe aktarın

>>> X, y = load_diabetes(return_X_y= True )

>>> regresör = DecisionTreeRegressor(random_state=0)

>>> cross_val_score(regresör, X, y, cv=10)

… # belge testi: +SKIP

…

dizi([-0.39…, -0.46…, 0.02…, 0.06…, -0.50…,

0.16…, 0.11…, -0.73…, -0.30…, -0.00…])

Sıradaki ne?

Ayrıca, Makine öğrenimi hakkında daha fazla bilgi edinmek istiyorsanız, çalışan profesyoneller için tasarlanmış ve 450+ saatlik zorlu eğitim, 30'dan fazla vaka çalışması ve ödev sunan IIIT-B & upGrad'ın Makine Öğrenimi ve AI'daki Yönetici PG Programına göz atın. , IIIT-B Mezun statüsü, 5+ pratik uygulamalı bitirme projesi ve en iyi firmalarla iş yardımı.