用简单的例子理解贝叶斯决策理论

介绍

我们在现实生活中会遇到很多分类问题。 例如，一家电子商店可能需要知道基于特定年龄的特定客户是否会购买计算机。 通过这篇文章，我们将介绍一种名为“贝叶斯决策理论”的方法，它可以帮助我们根据某个特征来决定是选择具有“x”概率的类还是选择具有“y”概率的相反类。

定义

贝叶斯决策理论是解决模式分类等各种问题的简单但基本的方法。 贝叶斯决策理论的全部目的是帮助我们选择成本最低“风险”的决策。 我们选择的任何决定总是存在某种风险。 我们将在本文后面介绍此分类所涉及的风险。

基本决定

让我们举一个例子，一家电子商店公司想知道客户是否要购买电脑。 所以我们有以下两个购买等级：

w1 - 是（客户将购买计算机）

w2 – 否（客户不会购买计算机）

现在，我们将查看客户数据库的过去记录。 我们会记下购买电脑的客户数量以及不购买电脑的客户数量。 现在，我们将计算客户购买计算机的概率。 让它成为 P(w1)。 类似地，客户不购买客户的概率为 P(w2)。

现在我们将为我们未来的客户做一个基本的比较。

对于一个新客户，

如果 P(w1) > P(w2)，那么客户将购买一台计算机 (w1)

并且，如果 P(w2) > P(w1)，则客户不会购买计算机 (w2)

在这里，我们已经解决了我们的决策问题。

但是，这种基本的决策方法有什么问题？ 好吧，你们中的大多数人可能都猜对了。 仅基于以前的记录，它将始终为所有未来的客户做出相同的决定。 这是不合逻辑和荒谬的。

因此，我们需要一些能够帮助我们为未来客户做出更好决策的东西。 我们通过引入一些功能来做到这一点。 假设我们添加了一个特征“x”，其中“x”表示客户的年龄。 现在有了这个附加功能，我们将能够做出更好的决定。

为此，我们需要知道贝叶斯定理是什么。

阅读：监督学习的类型

贝叶斯定理和决策理论

对于我们的类 w1 和特征“x”，我们有：

P(w1 | x) = P(x | w1) * P(w1) P(x)

这个公式中有4个术语需要我们理解：

1. Prior – P(w1) 是在观察数据之前 w1 为真的先验概率
2. 后验 – P(w1 | x) 是观察数据后 w1 为真的后验概率。
3. 证据 – P(x) 是数据的总概率
4. 似然性——P(x | w1) 是“x”提供的关于 w1 的信息

P(w1 | x) 读作 w1 给定 x 的概率

更准确地说，它是给定特定客户年龄的客户购买计算机的概率。

现在，我们准备好做出决定了：

对于一个新客户，

如果 P(w1 | x) > P(w2 | x)，那么客户将购买一台计算机 (w1)

并且，如果 P(w2 | x) > P(w1 | x)，那么客户不会购买计算机 (w2)

这个决定似乎更合乎逻辑和值得信赖，因为我们在这里有一些功能需要处理，而且我们的决定是基于我们新客户的特征以及过去的记录，而不是像以前的案例那样只是过去的记录。

现在，从公式中，您可以看到对于我们的类 w1 和 w2，我们的分母 P(x) 是恒定的。 因此，我们可以利用这个想法，形成另一种形式的决策，如下所示：

如果 P(x | w1)*P(w1) > P(x | w2)*P(w2)，那么客户将购买一台计算机 (w1)

并且，如果 P(x | w2)*P(w2) > P(x | w1)*P(w1)，则客户不会购买计算机 (w2)

我们可以在这里注意到一个有趣的事实。 如果不知何故，我们的先验概率 P(w1) 和 P(w2) 相等，我们仍然可以根据我们的似然概率 P(x | w1) 和 P(x | w2) 做出决定。 类似地，如果我们的似然概率相等，我们可以根据我们的先验概率 P(w1) 和 P(w2) 做出决定。

必读：机器学习中的回归模型类型

风险计算

如前所述，决策中总会存在一定程度的“风险”或错误。 因此，我们还需要确定决策中出错的概率。 这非常简单，我将在可视化方面进行演示。

让我们考虑一下我们有一些数据，并且我们已经根据贝叶斯决策理论做出了决定。

我们得到一个有点像下面的图表：

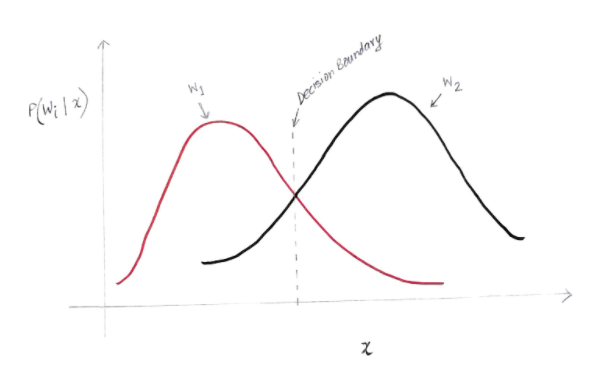
y 轴是后验概率 P(w(i) | x)，x 轴是我们的特征“x”。 两个类的后验概率相等的轴称为我们的决策边界。

所以在决策边界：

P(w1 | x) = P(w2 | x)

因此，在决策边界的左侧，我们决定支持 w1（购买计算机），而在决策边界的右侧，我们决定支持 w2（不购买计算机）。

但是，正如您在图中看到的那样，在决策边界的左侧有一些 w2 的非零幅度。 此外，在决策边界的右侧有一些 w1 的非零幅度。 另一个类对另一个类的这种扩展就是你所说的风险或概率错误。

概率误差的计算

为了计算类别 w1 的错误概率，我们需要在决策边界左侧的区域中找到类别为 w2 的概率。 类似地，类 w2 的错误概率是该类在决策边界右侧的区域中为 w1 的概率。

从数学上讲，类的最小误差：

w1 是 P(w2 | x)

对于 w2 类是 P(w1 | x)

你得到了你想要的概率错误。 很简单，不是吗？

那么现在的总误差是多少？

让我们将特征 x 的总错误概率表示为 P(E | x)。 特征 x 的总误差将是该特征 x 的所有错误概率的总和。 使用简单的集成，我们可以解决这个问题，我们得到的结果是：

P(E | x) = 最小值 (P(w1 | x) , P(w2 | x))

因此，我们的总错误概率是两个类的后验概率的最小值。 我们选择一个班级的最小值，因为最终我们将根据另一个班级做出决定。

结论

我们已经详细研究了贝叶斯决策理论的离散应用。 您现在知道贝叶斯定理及其术语。 您还知道如何在决策中应用贝叶斯定理。 您还学习了如何确定您做出的决定中的错误。

如果您有兴趣了解有关机器学习的更多信息，请查看 IIIT-B 和 upGrad 的机器学习和人工智能 PG 文凭，该文凭专为工作专业人士设计，提供 450 多个小时的严格培训、30 多个案例研究和作业、IIIT- B 校友身份、5 个以上实用的实践顶点项目和顶级公司的工作协助。