Verstehen der Bayes'schen Entscheidungstheorie mit einem einfachen Beispiel

Einführung

Im wirklichen Leben stoßen wir auf viele Klassifizierungsprobleme. Beispielsweise muss ein Elektronikgeschäft möglicherweise wissen, ob ein bestimmter Kunde basierend auf einem bestimmten Alter einen Computer kaufen wird oder nicht. In diesem Artikel stellen wir eine Methode namens „Bayessche Entscheidungstheorie“ vor, die uns dabei hilft, Entscheidungen zu treffen, ob wir basierend auf einem bestimmten Merkmal eine Klasse mit „x“-Wahrscheinlichkeit oder eine entgegengesetzte Klasse mit „y“-Wahrscheinlichkeit auswählen.

Definition

Die Bayes'sche Entscheidungstheorie ist ein einfacher, aber grundlegender Ansatz für eine Vielzahl von Problemen wie die Musterklassifizierung. Der gesamte Zweck der Bayes-Entscheidungstheorie besteht darin, uns bei der Auswahl von Entscheidungen zu helfen, die uns das geringste „Risiko“ kosten. Jede Entscheidung, die wir treffen, ist immer mit einem gewissen Risiko verbunden. Wir werden das mit dieser Klassifizierung verbundene Risiko später in diesem Artikel durchgehen.

Grundlegende Entscheidung

Nehmen wir ein Beispiel, bei dem ein Elektronikfachgeschäft wissen möchte, ob ein Kunde einen Computer kaufen wird oder nicht. Wir haben also die folgenden zwei Kaufklassen:

w1 – Ja (Kunde kauft einen Computer)

w2 – Nein (Kunde kauft keinen Computer)

Jetzt schauen wir uns die vergangenen Aufzeichnungen unserer Kundendatenbank an. Wir notieren die Anzahl der Kunden, die Computer kaufen, und auch die Anzahl der Kunden, die keinen Computer kaufen. Jetzt berechnen wir die Wahrscheinlichkeiten, dass Kunden einen Computer kaufen. Sei P(w1). Ebenso ist die Wahrscheinlichkeit, dass Kunden einen Kunden nicht kaufen, P(w2).

Jetzt werden wir einen grundlegenden Vergleich für unsere zukünftigen Kunden durchführen.

Für einen Neukunden,

Wenn P(w1) > P(w2), dann kauft der Kunde einen Computer (w1)

Und wenn P(w2) > P(w1), dann kauft der Kunde keinen Computer (w2)

Hier haben wir unser Entscheidungsproblem gelöst.

Aber was ist das Problem mit dieser grundlegenden Entscheidungsmethode? Nun, die meisten von Ihnen haben vielleicht richtig geraten. Basierend auf nur früheren Aufzeichnungen wird es immer die gleiche Entscheidung für alle zukünftigen Kunden geben. Das ist unlogisch und absurd.

Wir brauchen also etwas, das uns hilft, bessere Entscheidungen für zukünftige Kunden zu treffen. Wir tun dies, indem wir einige Funktionen einführen. Angenommen, wir fügen ein Merkmal „x“ hinzu, wobei „x“ das Alter des Kunden angibt. Mit dieser zusätzlichen Funktion können wir jetzt bessere Entscheidungen treffen.

Dazu müssen wir den Satz von Bayes kennen.

Lesen Sie: Arten von überwachtem Lernen

Satz von Bayes und Entscheidungstheorie

Für unsere Klasse w1 und Merkmal 'x' haben wir:

P(w1 | x) = P(x | w1) * P(w1) P(x)

Es gibt 4 Begriffe in dieser Formel, die wir verstehen müssen:

1. Prior – P(w1) ist die Prior-Wahrscheinlichkeit, dass w1 wahr ist, bevor die Daten beobachtet werden
2. Posterior – P(w1 | x) ist die Posterior-Wahrscheinlichkeit, dass w1 wahr ist, nachdem die Daten beobachtet wurden.
3. Beweis – P(x) ist die Gesamtwahrscheinlichkeit der Daten
4. Wahrscheinlichkeit – P(x | w1) ist die Information über w1, die von 'x' bereitgestellt wird

P(w1 | x) wird als Wahrscheinlichkeit von w1 bei gegebenem x gelesen

Genauer gesagt ist es die Wahrscheinlichkeit, dass ein Kunde einen Computer kauft, wenn man das Alter eines bestimmten Kunden berücksichtigt.

Jetzt sind wir bereit, unsere Entscheidung zu treffen:

Für einen Neukunden,

Wenn P(w1 | x) > P(w2 | x), dann kauft der Kunde einen Computer (w1)

Und wenn P(w2 | x) > P(w1 | x), dann kauft der Kunde keinen Computer (w2)

Diese Entscheidung erscheint logischer und vertrauenswürdiger, da wir hier einige Merkmale haben, an denen wir arbeiten müssen, und unsere Entscheidung auf den Merkmalen unserer neuen Kunden und auch früheren Aufzeichnungen und nicht nur früheren Aufzeichnungen wie in früheren Fällen basiert.

Aus der Formel können Sie nun ersehen, dass unser Nenner P(x) für unsere beiden Klassen w1 und w2 konstant ist. Wir können diese Idee also nutzen und eine andere Form der Entscheidung wie folgt bilden:

Wenn P(x | w1)*P(w1) > P(x | w2)*P(w2), dann kauft der Kunde einen Computer (w1)

Und wenn P(x | w2)*P(w2) > P(x | w1)*P(w1), dann kauft der Kunde keinen Computer (w2)

Wir können hier eine interessante Tatsache feststellen. Wenn unsere vorherigen Wahrscheinlichkeiten P(w1) und P(w2) irgendwie gleich sind, können wir unsere Entscheidung immer noch auf der Grundlage unserer Wahrscheinlichkeitswahrscheinlichkeiten P(x | w1) und P(x | w2) treffen. In ähnlicher Weise können wir, wenn unsere Likelihood-Wahrscheinlichkeiten gleich sind, Entscheidungen basierend auf unseren vorherigen Wahrscheinlichkeiten P(w1) und P(w2) treffen.

Muss gelesen werden: Typen von Regressionsmodellen beim maschinellen Lernen

Risikoberechnung

Wie bereits erwähnt, wird es immer ein gewisses Maß an „Risiko“ oder Fehlern geben, die bei der Entscheidung gemacht werden. Wir müssen also auch die Fehlerwahrscheinlichkeit einer Entscheidung bestimmen. Das ist sehr einfach und ich werde das anhand von Visualisierungen demonstrieren.

Nehmen wir an, wir haben einige Daten und wir haben eine Entscheidung gemäß der Bayes'schen Entscheidungstheorie getroffen.

Wir erhalten eine Grafik wie unten:

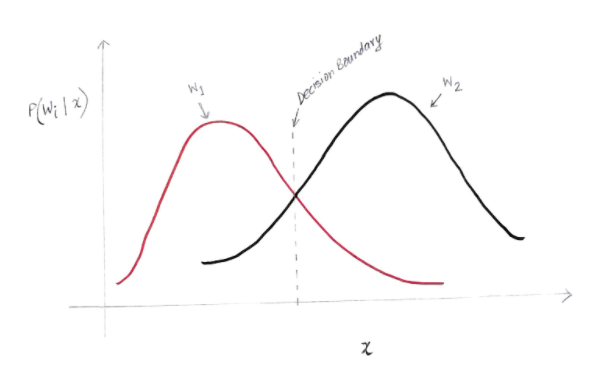
Die y-Achse ist die spätere Wahrscheinlichkeit P(w(i) | x) und die x-Achse ist unser Merkmal 'x'. Die Achse, auf der die A-posteriori-Wahrscheinlichkeit für beide Klassen gleich ist, wird als unsere Entscheidungsgrenze bezeichnet.

Also an der Entscheidungsgrenze:

P(w1 | x) = P(w2 | x)

Also entscheiden wir uns links von der Entscheidungsgrenze für w1 (Computer kaufen) und rechts von der Entscheidungsgrenze für w2 (keinen Computer kaufen).

Aber wie Sie in der Grafik sehen können, gibt es links von der Entscheidungsgrenze eine Größe von w2 ungleich Null. Außerdem gibt es rechts von der Entscheidungsgrenze eine Größe von w1 ungleich Null. Diese Erweiterung einer anderen Klasse über eine andere Klasse nennt man einen Risiko- oder Wahrscheinlichkeitsfehler.

Berechnung des Wahrscheinlichkeitsfehlers

Um die Irrtumswahrscheinlichkeit für die Klasse w1 zu berechnen, müssen wir die Wahrscheinlichkeit finden, dass die Klasse w2 in dem Bereich links von der Entscheidungsgrenze ist. In ähnlicher Weise ist die Fehlerwahrscheinlichkeit für die Klasse w2 die Wahrscheinlichkeit, dass die Klasse w1 in dem Bereich ist, der rechts von der Entscheidungsgrenze liegt.

Mathematisch gesehen ist der minimale Fehler für die Klasse:

w1 ist P(w2 | x)

Und für die Klasse w2 ist P(w1 | x)

Sie haben Ihren gewünschten Wahrscheinlichkeitsfehler erhalten. Einfach, nicht wahr?

Was ist nun der Gesamtfehler?

Lassen Sie uns die Wahrscheinlichkeit des Gesamtfehlers für ein Merkmal x mit P(E | x) bezeichnen. Der Gesamtfehler für ein Merkmal x wäre die Summe aller Fehlerwahrscheinlichkeiten für dieses Merkmal x. Durch einfache Integration können wir dies lösen und das Ergebnis ist:

P(E | x) = Minimum (P(w1 | x) , P(w2 | x))

Daher ist unsere Gesamtfehlerwahrscheinlichkeit das Minimum der A-posteriori-Wahrscheinlichkeit für beide Klassen. Wir nehmen das Minimum einer Klasse, weil wir letztendlich eine Entscheidung auf der Grundlage der anderen Klasse treffen werden.

Fazit

Wir haben uns die diskreten Anwendungen der Bayes'schen Entscheidungstheorie ausführlich angesehen. Sie kennen jetzt den Satz von Bayes und seine Begriffe. Sie wissen auch, wie man den Satz von Bayes anwendet, um eine Entscheidung zu treffen. Sie haben auch gelernt, wie Sie den Fehler in der von Ihnen getroffenen Entscheidung bestimmen können.

Wenn Sie mehr über maschinelles Lernen erfahren möchten, sehen Sie sich das PG-Diplom in maschinellem Lernen und KI von IIIT-B & upGrad an, das für Berufstätige konzipiert ist und mehr als 450 Stunden strenge Schulungen, mehr als 30 Fallstudien und Aufgaben bietet, IIIT- B-Alumni-Status, mehr als 5 praktische, praktische Abschlussprojekte und Jobunterstützung bei Top-Unternehmen.